.chứng minh : a // b bis
a) A1 = 50 độ
b) B2 = 130 độ
c) A1 + B2 = 180 độ
d) A2 + B1 = 180 độ
Những câu hỏi liên quan
Cho A1 = 50 độ, B1 = 130 độ
a, Chứng tỏ a//b
b, tính B2+A2?
c, Tính A2+A3+B4?
Cho A1=B1 Chứng minh a)A1=B3, A4=B2 b)A2=B2, A3=B3, A4=B4 c)A2+B1=180°,A4+B3=180°
giúp mik vs
a, \(\widehat{B}_1=\widehat{B_3}\) đối đỉnh
\(\widehat{A}_1=\widehat{B}_1\) theo bài đầu
Do đó \(\widehat{A_1}=\widehat{B_3}\)
Mặt khác,ta có \(\widehat{A_1}+\widehat{A_4}=180^0\) hai góc kề bù
=> \(\widehat{A_4}=180^0-\widehat{A_1}\) \((1)\)
Và \(\widehat{B_2}+\widehat{B_3}=180^0\) hai góc kề bù
=> \(\widehat{B_2}=180^0-\widehat{B_3}\) \((2)\)
\(\widehat{A_1}=\widehat{B_3}\) \((3)\)
Từ 1,2,3 ta có : \(\widehat{A_4}=\widehat{B_2}\)
b, \(\widehat{A_2}=\widehat{A_4}\) đối đỉnh
\(\widehat{A_4}=\widehat{B_2}\) theo câu a
Do đó : \(\widehat{A_2}=\widehat{B_2};\widehat{A_1}=\widehat{A_3}\) đối đỉnh
\(\widehat{A_1}=\widehat{B_3}\) câu a
Do đó \(\widehat{A_3}=\widehat{B_3}\). Mặt khác \(\widehat{B_2}=\widehat{B_4}\) hai góc đối đỉnh
\(\widehat{A_4}=\widehat{B_2}\) câu a . Do đó \(\widehat{A_4}=\widehat{B_4}\)
c, \(\widehat{B_1}+\widehat{B_2}=180^0\) hai góc kề bù
\(\widehat{A_1}=\widehat{B_1}\) theo đầu bài
Do đó \(\widehat{A_1}+\widehat{B_2}=180^0\)
Mặt khác \(\widehat{B_2}+\widehat{B_3}=180^0\) kề bù
\(\widehat{A_4}=\widehat{B_2}\) theo câu a . Do đó \(\widehat{A_4}+\widehat{B_3}=180^0\)
Đúng 0
Bình luận (0)
Trong hình bên, cho biết A1=B3. Chứng minh rằng:
a/A4=B2
b/A1=B1; A2=B2
c/A2+B1=\(^{180^0}\); A3+B4=\(^{180^0}\)
Trong hình 3.11 có
A
1
^
+
A
2
^
+
B
2
^
a
°
;
B
1
^
+
B
2
^
+
A
1...
Đọc tiếp
Trong hình 3.11 có A 1 ^ + A 2 ^ + B 2 ^ = a ° ; B 1 ^ + B 2 ^ + A 1 ^ = b ° , trong đó 180 ° < a ° < 360 ° ; 180 ° < b ° < 360 ° và a ° + b ° = 540 ° . Chứng tỏ rằng a // b
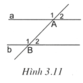
Ta có A 1 ^ + A 2 ^ + B 2 ^ = a ° ⇒ B 2 ^ = a ° − 180 ° (1)
B 1 ^ + B 2 ^ + A 1 ^ = b ° ⇒ A 1 ^ = b ° − 180 ° (2)
Từ (1) và (2), suy ra: B 2 ^ + A 1 ^ = a ° + b ° − 360 ° = 540 ° − 360 ° = 180 ° .
Mặt khác A 2 ^ + A 1 ^ = 180 ° (kề bù) nên B 2 ^ + A 1 ^ = A 2 ^ + A 1 ^ = 180 ° .
Suy ra B 2 ^ = A 2 ^ . Do đó a // b vì có cặp góc đồng vị bằng nhau
Đúng 0
Bình luận (0)
cho hình vẽ biết góc A3+B1180 độ,hãy so sánh góc A4 và B1?,góc A1 và B2, Góc A2 và B3 x y B A 1 2 3 4 2 1 3 4
Đọc tiếp
cho hình vẽ biết góc A3+B1=180 độ,hãy so sánh góc A4 và B1?,góc A1 và B2, Góc A2 và B3
Nếu a1b1=a2b2 thì: A. a1/a2=b1/b2 B. a1/a2=b2/b1 C. a1/b2=a2/b1 D. a1/b2=b1/a2
GYE4F4GGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGG
Đúng 0
Bình luận (0)
cho hình vẽ biết:
A1=5/7 A2
B2-B1=30 độ
a vuông góc với c
Tính:
a A1,A2
b B1,B2
c C1,C2
a) Biết A3= B1. CMR: A2 + B1= 180 độ
b) Bt A1 = B1. CM: A3 = B1; A2 = B4
c) Bt A2= B4 và A1= 72 độ. Tính các góc còn lại
a) Biết A3= B1. CMR: A2 + B1= 180 độ
b) Bt A1 = B1. CM: A3 = B1; A2 = B4
c) Bt A2= B4 và A1= 72 độ. Tính các góc còn lại
Đúng 0
Bình luận (0)
cHO HÌNH VẼ, BIẾT A1=B1
CHỨNG TỎ RẰNG: A)A1=B3 , A4=B2
B)A2=B2 , A1=B2 , A3=B4 , A4=B4
C)A4+B3=180
Tham khảo : Câu hỏi của huy nguyễn - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Trên hình biết a // b và góc B2=40 độ:
a) Tính góc A1
b) So sánh góc A3 và B1
c) Tính góc A2+B1
\(a,a//b\Rightarrow\widehat{B_2}+\widehat{A_1}=180^0\left(trong.cùng.phía\right)\\ \Rightarrow\widehat{A_1}=180^0-40^0=140^0\\ b,a//b\Rightarrow\widehat{A_1}=\widehat{B_1}\left(đồng.vị\right)\\ Mà.\widehat{A_1}=\widehat{A_3}\left(đối.đỉnh\right)\\ \Rightarrow\widehat{A_3}=\widehat{B_1}\\ c,Ta.có.\widehat{A_2}+\widehat{B_1}=\widehat{A_2}+\widehat{A_1}=180^0\left(kề.bù\right)\)
Đúng 1
Bình luận (1)
a. Ta có: a // b
=> \(\widehat{B_2}+\widehat{A_1}=180^o\) (2 góc trong cùng phía)
Mà \(\widehat{B_2}=40^o\)
=> \(\widehat{A_1}=180^o-40^o=140^o\)
b. Ta có: \(\widehat{A_1}=\widehat{B_3}\) (so le trong) (1)
Ta lại có: \(\left\{{}\begin{matrix}\widehat{A_1}=\widehat{A_3}\left(ĐĐ\right)\\\widehat{B_1}=\widehat{B_3}\left(ĐĐ\right)\end{matrix}\right.\) (2)
Từ (1) và (2), suy ra:
\(\widehat{A_3}=\widehat{B_1}\)
c. Ta có: a // b
=> \(\widehat{A_1}=\widehat{B_1}=140^o\) (đồng vị)
\(\widehat{B_2}=\widehat{A_2}=40^o\) (đồng vị)
=> \(\widehat{A_2}+\widehat{B_1}=140^o+40^o=180^o\)
Đúng 0
Bình luận (0)