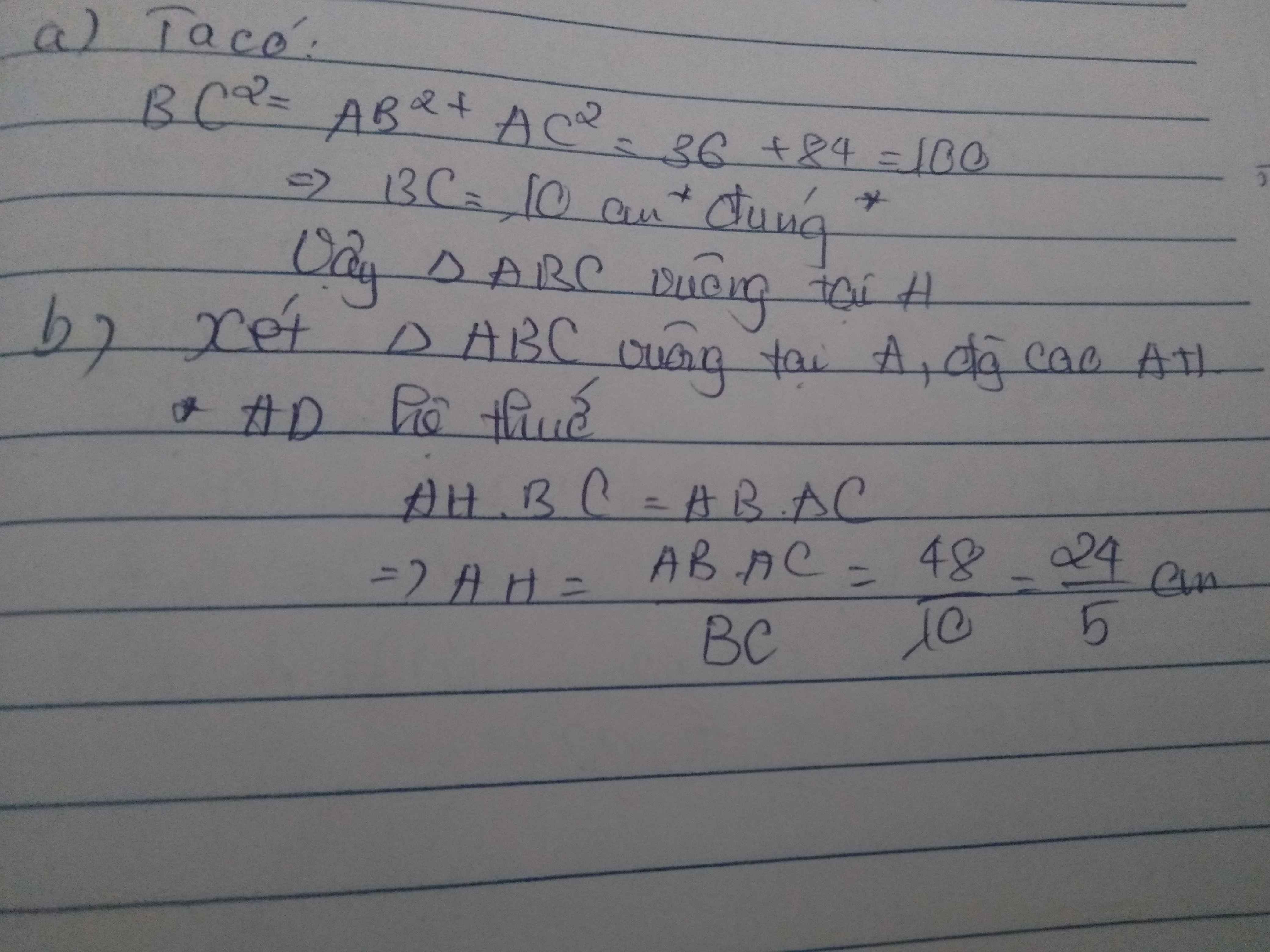Bài 1: Cho tam giác ABC, A= 90 độ, B=30 độ AB= 8cm, Giải tam giác ABC bạn nhớ kẻ hình giúp tớ nhé

Những câu hỏi liên quan
1)cho tam giác abc có a=90 độ,ab=8cm,c=30 độ
a)giải tam giác abc
b)tính chu vi và diện tích tam giác abc
2)cho tam giác abc có b=32 độ,c=54 độ,ac=11cm
a)tính bac=?
b)tinhs ab=? bc=?
ai biết giúp mình với,please cảm ơn nhiều :))
Cho tam giác ABC vuông tại A, biết AB = 8cm ; 𝐵̂ = 30 độ a) Giải tam giác ABC b) Kẻ phân giác AD. Đường cao AH. Tính diện tích tam giác ADH
a: Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan30^0\)
\(=\dfrac{8\sqrt{3}}{3}\left(cm\right)\)
\(\Leftrightarrow BC=\dfrac{16\sqrt{3}}{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
ai giúp mình giải bài toán này với được k ạ ( chi tiết hộ mình nhé)-bài 1: cho tam giác ABC có AB6cm; AC8cm; BC10cm.a, chứng minh tam giác ABC vuôngb, tính độ cao AH-bài 2: cho tam giác ABC có, AB12cm; AC16cm; BC20cma, chứng minh tam giác ABC vuôngb tính độ cao AHc, kẻ HD và HE lần lượt vuông góc AB , AC. Tính HD và HE.-Bài 3: cho tam giác ABC vuông tại A , đường cao AH, biết AH:AC3:5 và AB15cma, tính HB và HC b, gọi E, F lần lượt là hình chiếu của H trên AB và AC ; chứng minh AB.ACEF.BC-bài 4:...
Đọc tiếp
ai giúp mình giải bài toán này với được k ạ ( chi tiết hộ mình nhé)
-bài 1: cho tam giác ABC có AB=6cm; AC=8cm; BC=10cm.
a, chứng minh tam giác ABC vuông
b, tính độ cao AH
-bài 2: cho tam giác ABC có, AB=12cm; AC=16cm; BC=20cm
a, chứng minh tam giác ABC vuông
b tính độ cao AH
c, kẻ HD và HE lần lượt vuông góc AB , AC. Tính HD và HE.
-Bài 3: cho tam giác ABC vuông tại A , đường cao AH, biết AH:AC=3:5 và AB=15cm
a, tính HB và HC
b, gọi E, F lần lượt là hình chiếu của H trên AB và AC ; chứng minh AB.AC=EF.BC
-bài 4: cho tam giác ABC vuông tại A đường phân giác trong BD( DϵAC) cho AB=3cm; BC=5cm.
a, tính AC, AD,CD
b, tính BD
1.
a. Ta có: \(AB^2+AC^2=6^2+8^2=36+64=100\)
\(BC^2=10^2=100\)
\(\Rightarrow AB^2+AC^2=BC^2\) \(\Rightarrow\Delta\)ABC vuông tại A
b. \(\Delta\)ABC vuông tại A, đường cao AH. Ta có:
AB.AC = AH.BC
hay 6.8 = AH.10
=> AH = \(\dfrac{6.8}{10}=4.8\)
Đúng 2
Bình luận (0)
ai giúp mình giải bài toán này với được k ạ ( chi tiết hộ mình nhé)-bài 1: cho tam giác ABC có AB6cm; AC8cm; BC10cm.a, chứng minh tam giác ABC vuôngb, tính độ cao AH-bài 2: cho tam giác ABC có, AB12cm; AC16cm; BC20cma, chứng minh tam giác ABC vuôngb tính độ cao AHc, kẻ HD và HE lần lượt vuông góc AB , AC. Tính HD và HE.-Bài 3: cho tam giác ABC vuông tại A , đường cao AH, biết AH:AC3:5 và AB15cma, tính HB và HC b, gọi E, F lần lượt là hình chiếu của H trên AB và AC ; chứng minh AB.ACEF.BC-bài 4:...
Đọc tiếp
ai giúp mình giải bài toán này với được k ạ ( chi tiết hộ mình nhé)
-bài 1: cho tam giác ABC có AB=6cm; AC=8cm; BC=10cm.
a, chứng minh tam giác ABC vuông
b, tính độ cao AH
-bài 2: cho tam giác ABC có, AB=12cm; AC=16cm; BC=20cm
a, chứng minh tam giác ABC vuông
b tính độ cao AH
c, kẻ HD và HE lần lượt vuông góc AB , AC. Tính HD và HE.
-Bài 3: cho tam giác ABC vuông tại A , đường cao AH, biết AH:AC=3:5 và AB=15cm
a, tính HB và HC
b, gọi E, F lần lượt là hình chiếu của H trên AB và AC ; chứng minh AB.AC=EF.BC
-bài 4: cho tam giác ABC vuông tại A đường phân giác trong BD( DϵAC) cho AB=3cm; BC=5cm.
a, tính AC, AD,CD
b, tính BD
ai giúp mình giải bài toán này với được k ạ ( chi tiết hộ mình nhé)-bài 1: cho tam giác ABC có AB6cm; AC8cm; BC10cm.a, chứng minh tam giác ABC vuôngb, tính độ cao AH-bài 2: cho tam giác ABC có, AB12cm; AC16cm; BC20cma, chứng minh tam giác ABC vuôngb tính độ cao AHc, kẻ HD và HE lần lượt vuông góc AB , AC. Tính HD và HE.-Bài 3: cho tam giác ABC vuông tại A , đường cao AH, biết AH:AC3:5 và AB15cma, tính HB và HC b, gọi E, F lần lượt là hình chiếu của H trên AB và AC ; chứng minh AB.ACEF.BC-bài 4:...
Đọc tiếp
ai giúp mình giải bài toán này với được k ạ ( chi tiết hộ mình nhé)
-bài 1: cho tam giác ABC có AB=6cm; AC=8cm; BC=10cm.
a, chứng minh tam giác ABC vuông
b, tính độ cao AH
-bài 2: cho tam giác ABC có, AB=12cm; AC=16cm; BC=20cm
a, chứng minh tam giác ABC vuông
b tính độ cao AH
c, kẻ HD và HE lần lượt vuông góc AB , AC. Tính HD và HE.
-Bài 3: cho tam giác ABC vuông tại A , đường cao AH, biết AH:AC=3:5 và AB=15cm
a, tính HB và HC
b, gọi E, F lần lượt là hình chiếu của H trên AB và AC ; chứng minh AB.AC=EF.BC
-bài 4: cho tam giác ABC vuông tại A đường phân giác trong BD( DϵAC) cho AB=3cm; BC=5cm.
a, tính AC, AD,CD
b, tính BD
Cho tam giác ABC,A =90 độ,B= 60 độ .Tia phân giác A cắt BC tại D,kẻ AH vuông góc với BC.Các bạn vẽ hình giúp mình nhé
+/Xét tam giác: ABD và Tam Giác IBD.......... có BD chung,......... góc ABD =góc CBD ( Vì BD là phân giác góc ABC) .........,Lại cso góc BAD=BDI=90*(cái này thì theo giả thiết nhé)
----->> đến đây thì suy ra đc điều cần chứng minh chưa nhỉ hì^^ 2 tam giác ấy bằng nhau theo trường hợp cạnh huyền góc nhọn....đúng chưa nào.
Đúng 0
Bình luận (0)
Cho tam giác abc ( a=90 độ). giải tam giác vuông abc biết a)AB =30cm , acb=30 độ b) AB=20cm ;AC=13cm
a.
Trong tam giác vuông ABC:
\(tan\widehat{ACB}=\dfrac{AB}{AC}\Rightarrow AC=AB.tan\widehat{ACB}=30.tan30^0=10\sqrt{3}\left(cm\right)\)
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=20\sqrt{3}\left(cm\right)\)
\(\widehat{ABC}=90^0-\widehat{ACB}=60^0\)
b.
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{569}\left(cm\right)\)
\(tan\widehat{ABC}=\dfrac{AC}{AB}=\dfrac{13}{20}\Rightarrow\widehat{ABC}\approx33^0\)
\(\widehat{ACB}=90^0-\widehat{ABC}=57^0\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Giải tam giác vuông ABC trong các trường hợp sau:
a) BC = 10cm,góc C= 30 độ. b) AB=8cm và góc B=30 độ ?
a: \(\widehat{B}=90^0-30^0=60^0\)
XétΔABC vuông tại A có
\(\sin C=\dfrac{AB}{BC}\)
nên AB=5cm
=>\(AC=5\sqrt{3}\left(cm\right)\)
b: \(\widehat{C}=90^0-30^0=60^0\)
Xét ΔABC vuông tại A có
\(\sin C=\dfrac{AB}{BC}\)
hay \(BC=16\sqrt{3}\left(cm\right)\)
=>\(AC=8\sqrt{3}\left(cm\right)\)
Đúng 1
Bình luận (0)
cho tam giác ABC có góc A bằng 90 độ đường cao AH,AB=6cm,AC=8cm a) chứng minh tam giác ABC đồng dạng tam giác CAB b)Tính BC,AH c) kẻ HD vuông AB D thuộc AB , HE vuông AC E thuộc AC chúng minh tam giác AED đồng dạng với tam giác ABC
CÁC BN ƠI GIÚP MK VS CHO MK LM ĐCUONG CÁC BN ƠI LM ỚN GIÚP MK VS\
CHO MK LỜI GIẢI CHI TIẾT VÀ HÌNH VẼ NỮA
LM ƠN GIÚP MK VS
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔHBA\(\sim\)ΔABC
Suy ra: BH/BA=BA/BC
hay \(BA^2=BH\cdot BC\)
b: \(AH=\sqrt{HB\cdot HC}=6\left(cm\right)\)
\(AB=\sqrt{BH\cdot BC}=2\sqrt{13}\left(cm\right)\)
c: Xét ΔAHB vuông tại H có HF là đường cao
nên \(AF\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)
hay AF/AC=AE/AB
Xét ΔAFE vuông tại A và ΔACB vuông tại A có
AF/AC=AE/AB
Do đó:ΔAFE\(\sim\)ΔACB
Đúng 2
Bình luận (1)