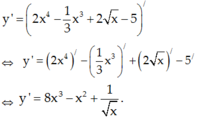Giair phươg trình 2x4-13x3+24x2-13x+2=0

Những câu hỏi liên quan
(2x4 – 13x3 + 15x2 +11x - 3) : (x2 - 4x - 3)
Tính đạo hàm của hàm số sau
y
2
x
4
-
1
3
x
3
+
2
x
-
5
Đọc tiếp
Tính đạo hàm của hàm số sau y = 2 x 4 - 1 3 x 3 + 2 x - 5
![]()
![]()
![]()
![]()
Tính đạo hàm của hàm số sau
y
2
x
4
-
1
3
x
3
+
2
x
-
36
D: Tất cả sai
Đọc tiếp
Tính đạo hàm của hàm số sau y = 2 x 4 - 1 3 x 3 + 2 x - 36
![]()
![]()
![]()
D: Tất cả sai
tìm x nguyên để:
(2x4-13x3+15x2+11x-4)⋮(x2-4x-3)
tìm m để phươg trình x2 - 2(2m+1)x+4m2 +4m=0 có hai nghiệm phân biệt x1,x2.
chứng minh rằng: (x12-4mx1+4m2)(x22-4mx2+4m2)=0
Ta có:
\(x^2-2\left(2m+1\right)x+4m^2+4m=0\\ \Leftrightarrow\left(x^2-2mx\right)-2\left(m+1\right)x+4m\left(m+1\right)=0\\ \Leftrightarrow x\left(x-2m\right)-2\left(m+1\right)\left(x-2m\right)=0\\ \Leftrightarrow\left(x-2m\right)\left(x-2m-2\right)=0\Leftrightarrow x_1=2m;...or...x_2=2m\)
\(\Rightarrow\left(x_1-2m\right)\left(x_2-2m\right)=0\Leftrightarrow\left(x_1-2m\right)^2\left(x_2-2m\right)^2=0\Leftrightarrow\left(x_1^2-4mx_1+4m^2\right)\left(x_2^2-4mx_2+4m^2\right)=0\)
Đúng 1
Bình luận (0)
Giải phương trình
e) x4 -4x3-8x2+8x=0
f) 2x2+3xy+y2=0
g) 2x4-x3-9x2+13x-5=0
h) (x+1)(x+3)(x+5)(x+7)+15=0
e: =>x(x^3-4x^2-8x+8)=0
=>x[(x^3+8)-4x(x+2)]=0
=>x(x+2)(x^2-2x+4-4x)=0
=>x(x+2)(x^2-6x+4)=0
=>\(x\in\left\{0;-2;3+\sqrt{5};3-\sqrt{5}\right\}\)
g: =>2x^4+5x^3-6x^3-15x^2+6x^2+15x-2x-5=0
=>(2x+5)(x^3-3x^2+3x-1)=0
=>(2x+5)(x-1)^3=0
=>x=1 hoặc x=-5/2
h: =>(x^2+8x+7)(x^2+8x+15)+15=0
=>(x^2+8x)^2+22(x^2+8x)+120=0
=>(x^2+8x+10)(x^2+8x+12)=0
=>(x^2+8x+10)(x+2)(x+6)=0
=>\(x\in\left\{-2;-6;-4+\sqrt{6};-4-\sqrt{6}\right\}\)
Đúng 0
Bình luận (0)
Kiểm tra lại tích (x2 – 4x – 3)(2x2 – 5x + 1) có bằng (2x4 - 13x3 + 15x2 + 11x – 3) hay không.
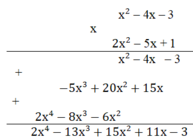
Vậy (x2 – 4x – 3)(2x2 – 5x + 1) = 2x4 - 13x3 + 15x2 + 11x – 3
Đúng 0
Bình luận (0)
Phân tích thành nhân tử:
a) x 3y 3 + x2y 2 + 4
b) 2x4 - 5x3 + 2x2 - x + 2
c) (x - 3)( x - 5)( x - 6)( x-10) - 24x2
d) (a + b + c)(ab + bc + ca)-abc
làm ơn cứu với
Giải các phương trình: 2x4 + 3x2 – 2 = 0
2x4 + 3x2 – 2 = 0 (1)
Đặt x2 = t, t ≥ 0.
(1) trở thành: 2t2 + 3t – 2 = 0 (2)
Giải (2) :
Có a = 2 ; b = 3 ; c = -2
⇒ Δ = 32 – 4.2.(-2) = 25 > 0
⇒ (2) có hai nghiệm
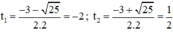
t1 = -2 < 0 nên loại.
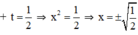
Vậy phương trình có tập nghiệm 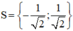
Đúng 0
Bình luận (0)