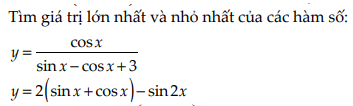mọi người ơi giúp mình bài 3 với

Những câu hỏi liên quan
Mọi người ơi giúp mình 3 bài này với mình cần gấp gấp lắm ạ , tối nay mình phải nộp rồi ạ , cảm ơn mọi người❤️
Tỉ lệ \(x=\dfrac{y}{-5}\)
x -4 -1 2 3
y 20 5 -10 -15
Đúng 0
Bình luận (0)
mọi người ơi giúp mình bài này với , làm đc bài nào thì giúp mình nha :
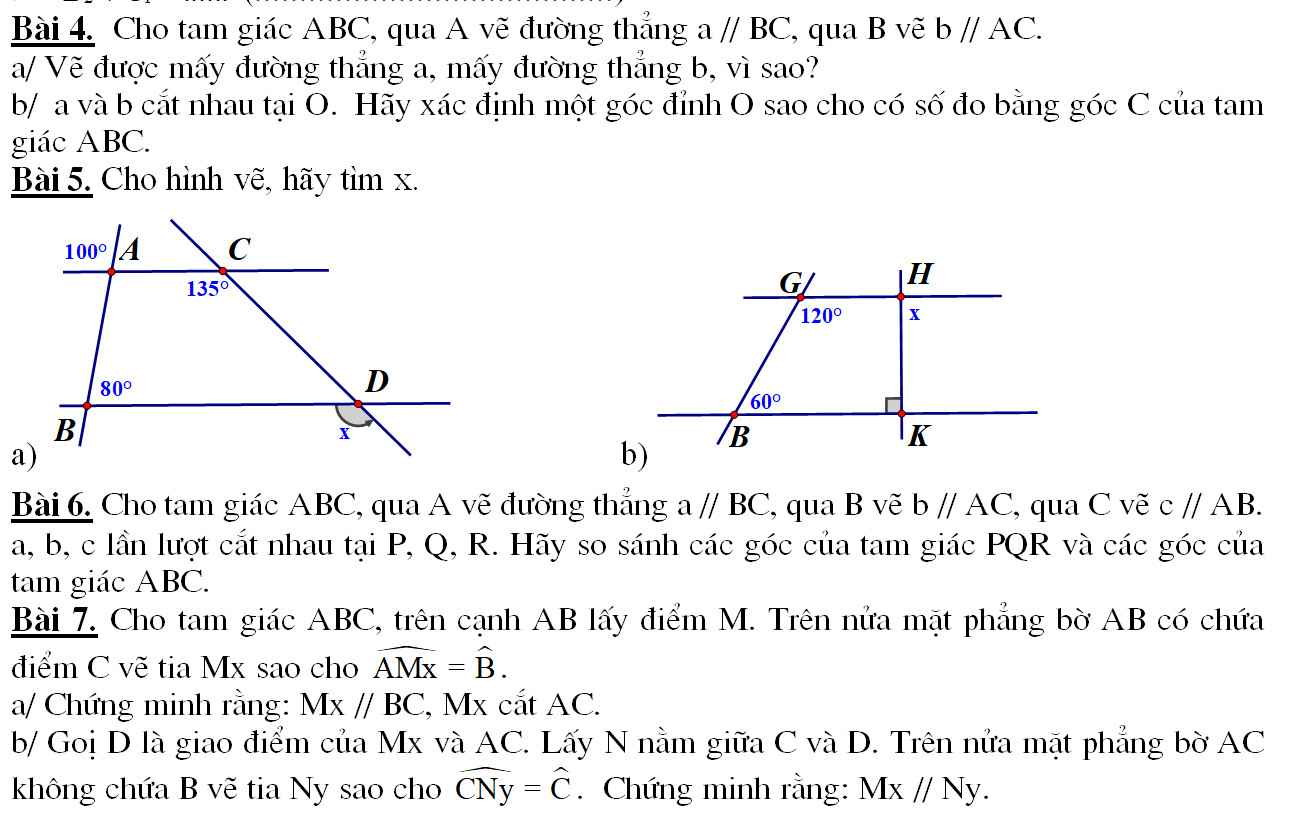
Bài 5:
Ta có : \(\widehat{A_1}+\widehat{A_3}=180^o\) (kề bù)
\(100^o+\widehat{A_3}=180^o\)
\(\widehat{A_3}=80^o\)
Ta có: \(\widehat{A_3}=\widehat{B_1}=80^o\)
\(\widehat{A_3}\) và \(\widehat{B_1}\) ở vị trí đồng vị
\(\Rightarrow AC//BD\)
\(\Rightarrow\widehat{C}_1=\widehat{D_1}=135^o\) (đồng vị)
\(x=135^o\)
b)
Ta có: \(\widehat{G_1}+\widehat{B_1}=180^o\left(120^o+60^o=180^o\right)\)
\(\widehat{G_1}\) và \(\widehat{B_1}\) ở vị trí trong cùng phía
\(\Rightarrow QH//BK\)
\(\Rightarrow\widehat{H_1}=\widehat{K_1}=90^o\)(so le)
\(x=90^o\)
Đúng 1
Bình luận (0)
Mọi người ơi giúp mình làm từ bài 44 đến 50 với nha mọi người mình cảm ơn nhiều
4: Đặt \(x=\dfrac{a+b}{a-b};y=\dfrac{b+c}{b-c};z=\dfrac{c+a}{c-a}\).
Ta có \(\left(x+1\right)\left(y+1\right)\left(z+1\right)=\dfrac{2a.2b.2c}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}=\left(x-1\right)\left(y-1\right)\left(z-1\right)\)
\(\Rightarrow xy+yz+zx=-1\).
Bất đẳng thức đã cho tương đương:
\(x^2+y^2+z^2\ge2\Leftrightarrow\left(x+y+z\right)^2-2\left(xy+yz+zx\right)-2\ge0\Leftrightarrow\left(x+y+z\right)^2\ge0\) (luôn đúng).
Vậy ta có đpcm
Đúng 3
Bình luận (1)
mình xí câu 45,47,51 :>
45. a) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1}{a}+\dfrac{4}{2b}\ge\dfrac{\left(1+2\right)^2}{a+2b}=\dfrac{9}{a+2b}\left(đpcm\right)\)
Đẳng thức xảy ra <=> a=b
b) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{b}\ge\dfrac{\left(1+1+1\right)^2}{a+b+b}=\dfrac{9}{a+2b}\)(1)
\(\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{c}\ge\dfrac{\left(1+1+1\right)^2}{b+c+c}=\dfrac{9}{b+2c}\)(2)
\(\dfrac{1}{c}+\dfrac{1}{a}+\dfrac{1}{a}\ge\dfrac{\left(1+1+1\right)^2}{c+a+a}=\dfrac{9}{c+2a}\)(3)
Cộng (1),(2),(3) theo vế ta có đpcm
Đẳng thức xảy ra <=> a=b=c
Đúng 2
Bình luận (0)
47. Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{\left(a+b\right)^2}{c}+\dfrac{\left(b+c\right)^2}{a}+\dfrac{\left(c+a\right)^2}{b}\ge\dfrac{\left(a+b+b+c+c+a\right)^2}{a+b+c}=\dfrac{\left[2\left(a+b+c\right)\right]^2}{a+b+c}=\dfrac{4\left(a+b+c\right)^2}{a+b+c}=4\left(a+b+c\right)\)(đpcm)
Đẳng thức xảy ra <=> a=b=c
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Mọi người ơi, mình chưa biết giải bài này:(( Mọi người giúp mình với, mình cảm ơn rất nhiều ạ😭 
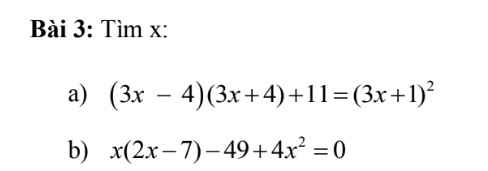
giúp mình bài này với mọi người ơi :((
b: \(\Leftrightarrow\left(2x-7\right)\left(3x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-\dfrac{7}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)

giúp mình bài này với mọi người ơi
a: Xét tứ giác AEDF có
AE//DF
AF//DE
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật
Đúng 1
Bình luận (0)
a) Vì DE//AB nên DE⊥AC và DF//AC nên DF⊥AB
Vì AED=AFD=EAF=900AED=AFD=EAF=900 nên AEDF là hcn
b) Vì E là trung điểm MD và AC nên AMCD là hbh
Mà AC⊥DE nên AMCD là hthoi
c) Vì D là trung điểm BC và AK và BAC=900BAC=900 nên ABKC là hcn
Để ABKC là hv thì AB=AC hay tam giác ABC vuông cân tại A
Đúng 1
Bình luận (1)
Mọi người ơi giúp mình bài này với 
Mọi người ơi giúp mình bài này với
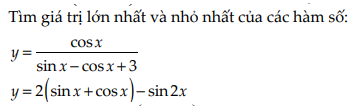
Mọi người ơi giúp mình bài này với