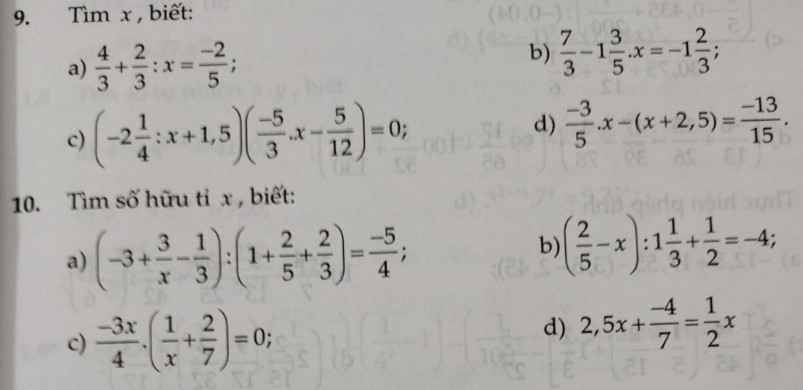 Giúp em với . Em cảm ơn nhiều
Giúp em với . Em cảm ơn nhiều

Những câu hỏi liên quan
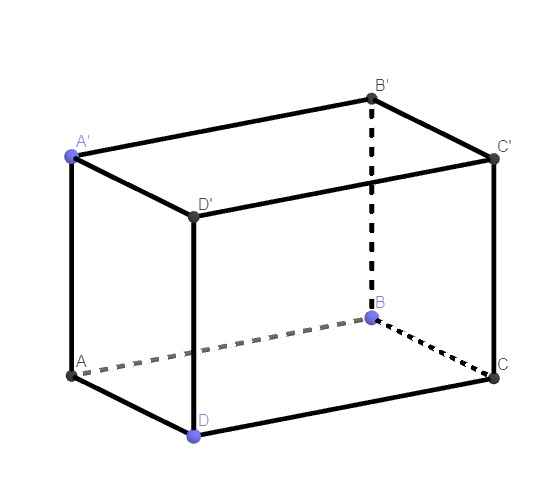
mọi người giải giúp em câu 71,74 với
em cảm ơn mọi người nhiều vẽ hình dùm em luôn em cảm ơn
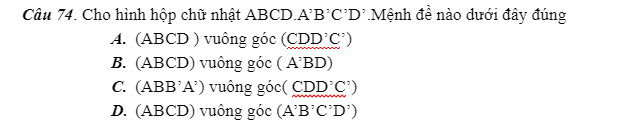
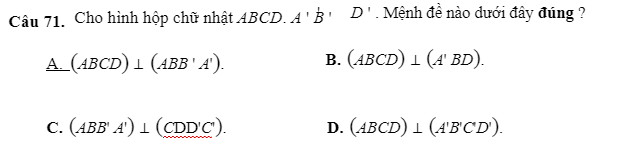
71.
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
74.
\(\left\{{}\begin{matrix}DD'\perp\left(ABCD\right)\\DD'\in\left(CDD'C'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(CDD'C'\right)\)
Đúng 0
Bình luận (0)
Giúp em với ạ ! Em cảm ơn nhiều
Xem thêm câu trả lời
Giúp em với ạ em cảm ơn nhiều
Giúp em với ạ ! Em cảm ơn nhiều!




Giúp em với ạ, Em cảm ơn nhiều
Giúp em với ạ! Em cảm ơn nhiều
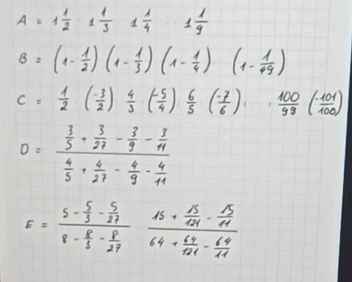
 giúp em với em cảm ơn nhiều ạ
giúp em với em cảm ơn nhiều ạ
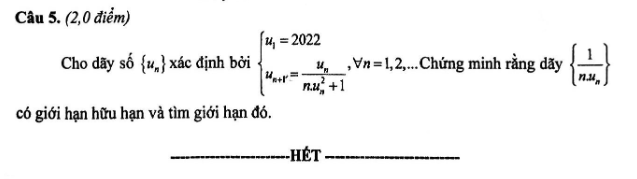
\(\dfrac{1}{u_{n+1}}=\dfrac{1}{u_n}+nu_n\)
Đặt \(v_n=\dfrac{1}{u_n}\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{1}{2022}\\v_{n+1}=v_n+\dfrac{n}{v_n}\end{matrix}\right.\) và \(\left\{\dfrac{1}{nu_n}\right\}=\left\{\dfrac{v_n}{n}\right\}\)
Ta sẽ chứng minh \(v_n\ge n\) với \(n>1\)
Với \(n=2\Rightarrow v_2=v_1+2022>2\) (đúng)
Giả sử điều đó đúng với \(n=k>1\) hay \(v_k\ge k\)
Ta cần chứng minh \(v_{k+1}\ge k+1\)
Thật vậy, do \(v_k\ge k\), đặt \(v_k=k+\alpha\) với \(\alpha\ge0\)
Khi đó: \(v_{k+1}=v_k+\dfrac{k}{v_k}=k+\alpha+\dfrac{k}{k+\alpha}=k+\dfrac{k\alpha+\alpha^2+k}{k+\alpha}\ge k+\dfrac{\alpha+k}{k+\alpha}=k+1\) (đpcm)
Tương tự, ta quy nạp chứng minh được \(v_n\le n+v_2\) với \(n>1\) (do \(v_2\) số xấu nên ko ghi)
Kiểm tra với \(n=2\Rightarrow v_2\le2+v_2\) (đúng)
Giả sử \(v_k\le k+v_2\)
\(\Rightarrow v_{k+1}=v_k+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{k}=k+1+v_2\) (đpcm)
\(\Rightarrow n\le v_n\le n+v_2\) \(\Rightarrow1\le\dfrac{v_n}{n}\le\dfrac{n+v_2}{n}\)
Sử dụng định lý kẹp, dễ dàng suy ra \(\lim\left\{\dfrac{v_n}{n}\right\}=1\)
Đúng 1
Bình luận (0)
Giúp em với ạ em cảm ơn nhiều 
Giúp em với ạ em cảm ơn nhiều .
1 are - go
2 don't go
3 is - goes
4 doesn't go
5 is - are
6 is
7 are
8 is - is taking
9 is - works
10 isn't working - is playing
11 do you do - watch
12 are you doing - am watching
13 does Lan do - watches
14 is Lan doing - is watching
15 doesn't work - works
16 does your mother travel
Đúng 0
Bình luận (0)













