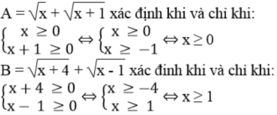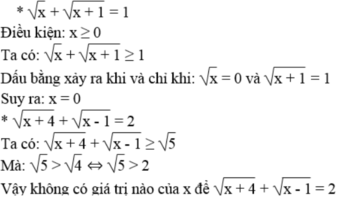Tìm x biết : x + 1 = 1

Những câu hỏi liên quan
tìm x,y thuộc Z ,biêt: (2x-1).(2x+1)=-35
tìm c,y thuộc Z , biết: (x+1)^2 + (y+1)^2 + (x-y)^2 =2
tìm x,y thuộc Z, biết: (x^2-8).(x^2-15)<0
tìm x,y thuộc Z biết: x=6.y và|x|-|y|=60
tìm a,b thuộc Z biết: |a|+|b|<2
1. Tìm X, biết: x - \(\dfrac{2}{3}\) x ( X + 9 ) = 1
2. Tìm X, biết: X - \(\dfrac{11}{15}\) = \(\dfrac{3+X}{5}\)
\(1.x-\dfrac{2}{3}\times\left(x+9\right)=1\)
\(x-\dfrac{2}{3}\times x-6=1\)
\(x\times\left(1-\dfrac{2}{3}\right)=7\)
\(x\times\dfrac{1}{3}=7\)
\(x=21\)
\(2.x-\dfrac{11}{15}=\dfrac{3+x}{5}\)
\(\dfrac{15x}{15}-\dfrac{11}{15}=\dfrac{9+3x}{15}\)
\(15x-11=9+3x\)
\(12x=20\)
\(x=\dfrac{5}{3}\)
Đúng 3
Bình luận (0)
a, Tìm x biết : (x+1) + (x+2) + ... + (x+100) = 5750
b, Tìm các số tự nhiên x,y biết : (x+1) . (2y-5)=143
`(x+1) + (x+2) + ... + (x+100) = 5750`
Số số ngoặc trong phép tính là:
`(100 - 1) : 1 + 1 = 100` (ngoặc)
`=> 100x + (1+2+3+...+100) = 5750`
`=> 100x + ((100 + 1) . 100 : 2) = 5750`
`=> 100x + 5050 = 5750`
`=> 100x = 200`
`=> x = 2`
`(x+1) . (2y-5) = 143`
`=> (2y-5) ∈ Ư(143)`
mà `2y-5 lẻ`
`=> 2y-5 ∈ {-1;-11;1;11} => y = {2;-3;3;8}`
mà `y ∈ N => y = {2;3;8}`
`=> x+1 ∈ {-143;143;13}`
`=> x ∈ {-144;142;12}`
mà `x ∈ N => x ∈ {142;12}`
Vậy `(x;y) = (142;3);(12;8)`
(Chúc bạn học tốt)
Đúng 2
Bình luận (1)
a) Ta có: \(\left(x+1\right)+\left(x+2\right)+...+\left(x+100\right)=5750\)
\(\Leftrightarrow100x+5050=5750\)
\(\Leftrightarrow100x=700\)
hay x=7
Đúng 0
Bình luận (0)
Cho biểu thức C =( \(\dfrac{2x^2+1}{x^3-1}-\dfrac{1}{x-1}\)):(1-\(\dfrac{x^2-2}{x^2+x+1}\))
a) Rút gọn C
b) Tính giá trị của C biết |1-x| +2 =3(x+1)
c) Tìm x nguyên để C nguyên
d) Tìm x biết |C| > C
e) Tìm x để C2-C + 1 đạt giá trị nhỏ nhất
\(C=\left(\dfrac{2x^2+1}{x^3-1}-\dfrac{1}{x-1}\right)\div\left(1-\dfrac{x^2-2}{x^2+x+1}\right)\)
ĐKXĐ: \(x\ne1\)
\(C=[\left(\dfrac{2x^2+1}{(x-1)\left(x^2+x+1\right)}-\dfrac{1}{x-1}\right)]\div\left(1-\dfrac{x^2-2}{x^2+x+1}\right)\)
\(\Leftrightarrow C=[\left(\dfrac{2x^2+1}{(x-1)\left(x^2+x+1\right)}-\dfrac{1\left(x^2+x+1\right)}{(x-1)\left(x^2+x+1\right)}\right)]\div[\dfrac{(x-1)\left(x^2+x+1\right)}{(x-1)\left(x^2+x+1\right)}-\dfrac{(x^2-2)(x-1)}{(x^2+x+1)\left(x-1\right)}]\)
\(\Rightarrow C=\left[2x^2+1-1\left(x^2+x+1\right)\right]\div\left[\left(x-1\right)\left(x^2+x+1\right)-\left(x-1\right)\left(x^2-2\right)\right]\)
\(\Rightarrow C=(2x^2+1-x^2-x-1)\div\left[\left(x-1\right)\left(x^2+x+1-x^2+2\right)\right]\)
\(\Rightarrow C=\left(x^2-x\right)\div\left[\left(x-1\right)\left(x+3\right)\right]\)
Đúng 2
Bình luận (0)
a)tìm x biết: 5^x-1 + 5^x-3= 650
b)tìm x biết: gttd x+1 +gttd x+2 +.......+gttd x+100=605x (gttd: giá trị tuyệt đối)
c) tìm x,y biết : (2x+1)/5=(4y-5)/9=(2x+4y-4)/7x
a) \(5^{x-1}+5^{x-3}=650\)
\(\Rightarrow5^x\left(\frac{1}{5}+\frac{1}{125}\right)=650\)
\(\Rightarrow5^x=650:\frac{26}{125}\)
\(\Rightarrow5^x=3125\)
\(\Rightarrow5^x=5^5\)
\(\Rightarrow x=5\)
1, Tìm x, biết \(x^2\) – 36 = 0
A. x = 6. B. x = -6.
C. x = 6; x = -6. D. x = 36 hoặc x = - 36.
2, Tìm x, biết \(x^3\) – 3\(x^2\) + 3x - 1 = 0
A. x = 1. B. x = -1. C. x = 0. D. x = 2.
Tìm x biết : |3 - |x-1| | = 2
Tìm x, y biết 4 |x+3| + |2y - 1| = 0
Bài 1 : Tìm x , biết :
a. |x-1|+|x-2|+....+|x-8| = 22
b. |x-1|+|x-2|+|x-3|+...+|x-100| = 2500
Bài 2 :
Tìm x , biết :
|x+1|+|x+2|+....+|x+100| = 605.x
Giúp tớ với ?
............................. Đấng Ed bảo ko chắc cho lắm nên sai thì sr nhé -,-
\(a)\)\(\left|x-1\right|+\left|x-2\right|+...+\left|x-8\right|=22\)
+) Với \(x\ge8\) ta có :
\(x-1+x-2+...+x-8=22\)
\(\Leftrightarrow\)\(8x-36=22\)
\(\Leftrightarrow\)\(x=\frac{29}{4}\)( không thỏa mãn )
+) Với \(x< 1\) ta có :
\(1-x+2-x+...+8-x=22\)
\(\Leftrightarrow\)\(36-8x=22\)
\(\Leftrightarrow\)\(x=\frac{7}{4}\) ( không thỏa mãn )
Vậy không có x thỏa mãn đề bài
\(b)\)\(\left|x-1\right|+\left|x-2\right|+\left|x-3\right|+...+\left|x-100\right|=2500\)
+) Với \(x\ge100\) ta có :
\(x-1+x-2+x-3+...+x-100=2500\)
\(\Leftrightarrow\)\(100x-5050=2500\)
\(\Leftrightarrow\)\(x=\frac{151}{2}\) ( không thỏa mãn )
+) Với \(x< 1\) ta có :
\(1-x+2-x+3-x+...+100-x=2500\)
\(\Leftrightarrow\)\(5050-100x=2500\)
\(\Leftrightarrow\)\(x=\frac{51}{2}\) ( không thỏa mãn )
Vậy không có x thỏa mãn đề bài
Bài 2 :
+) Với \(x\ge-1\) ta có :
\(x+1+x+2+...+x+100=605x\)
\(\Leftrightarrow\)\(100x+5050=605x\)
\(\Leftrightarrow\)\(x=10\) ( thỏa mãn )
+) Với \(x< -100\) ta có :
\(-x-1-x-2-...-x-100=605x\)
\(\Leftrightarrow\)\(-100x-5050=605x\)
\(\Leftrightarrow\)\(x=\frac{-1010}{141}\) ( không thỏa mãn )
Vậy \(x=10\)
~ Đấng phắn ~
Đúng 0
Bình luận (0)
Tìm điều kiện xác định của các biểu thức sau:
A
x
+
x
+
1
;
B
x
+
4
+
x
-
1...
Đọc tiếp
Tìm điều kiện xác định của các biểu thức sau:
A = x + x + 1 ; B = x + 4 + x - 1
Tìm x, biết: x + x + 1 = 1 ; x + 4 + x - 1 = 2
a) Tìm x,y biết x/5 =y/3 và x^2+ y^2 =4
b) Tìm x biết x-2/x-1 = x+4/x+1
cảm ơn mọi người nhìu nha!!!