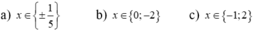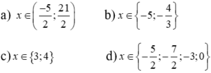Giải phương trình x2 - 2x +10=0

Những câu hỏi liên quan
Giải các phương trình sau:
b) x 2 - 5 + 2 x + 10 = 0
b) x 2 - ( 5 + 2 )x + 10 = 0
a = 1; b = 5 + 2 ; c = 10
Δ = b2 - 4ac = ( 5 + 2 )2 - 4.1. 10 = 5 + 2 10 + 2 - 4 10
= 5 - 2 10 + 2 = ( 5 - 2 )2 > 0
⇒ ∆ = 5 - 2
Phương trình đã cho có 2 nghiệm phân biệt
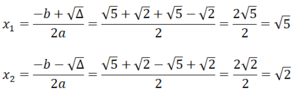
Vậy tập nghiệm của phương trình là S = { 5 ; - 2 }
Đúng 0
Bình luận (0)
giải phương trình tích :
a) ( 2x - 10 ) ( 5x + 25) = 0
b) ( x + 15) ( x - 2 ) = 0
c) x2 - 7x =0
a: (2x-10)(5x+25)=0
=>2x-10=0 hoặc 5x+25=0
=>x=5 hoặc x=-5
b: (x+15)(x-2)=0
=>x+15=0 hoặc x-2=0
=>x=-15 hoặc x=2
c: =>x(x-7)=0
=>x=0 hoặc x=7
Đúng 1
Bình luận (0)
a, (2x - 10) (5x + 25) = 0
⇒ 2x - 10 = 0 hoặc 5x + 25 = 0
⇒ x = 5 hoặc x = -5
b, (x + 15) (x - 2) = 0
⇒ x + 15 = 0 hoặc x - 2 = 0
⇒ x = -15 hoặc x = 2
c: =>x(x-7)=0
=>x=0 hoặc x=7
Đúng 1
Bình luận (0)
1 Trong các phương trình sau, phương trình nào vô nghiệm:
A. x2 – 2x + 2 = 0 B. x2 – 2x + 1 = 0
C. x2 – 2x = 0 D. 2x – 10 = 2x – 10
2 Phương trình nào sau đây có 1 nghiệm :
A. x2 – 3 x = 0 B. 2x + 1 =1 +2x
C. x ( x – 1 ) = 0 D. (x + 2)(x2 + 1) = 0
Hãy giải các phương trình sau đây :
1, x2 - 4x + 4 = 0
2, 2x - y = 5
3, x + 5y = - 3
4, x2 - 2x - 8 = 0
5, 6x2 - 5x - 6 = 0
6,( x2 - 2x )2 - 6 (x2 - 2x ) + 5 = 0
7, x2 - 20x + 96 = 0
8, 2x - y = 3
9, 3x + 2y = 8
10, 2x2 + 5x - 3 = 0
11, 3x - 6 = 0
1) Ta có: \(x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\)
hay x=2
Vậy: S={2}
Đúng 1
Bình luận (0)
Hãy cho biết phương trình nào trong các phương trình sau đây là phương trình đường tròn:
2x2 + y2 – 8x + 2y – 1 = 0;
x2 + y2 + 2x – 4y – 4 = 0;
x2 + y2 – 2x – 6y + 20 = 0;
x2 + y2 + 6x + 2y + 10 = 0.
+ 2x2 + y2 – 8x + 2y – 1 = 0 không phải phương trình đường tròn vì hệ số của x2 khác hệ số của y2.
+ Phương trình x2 + y2 + 2x – 4y – 4 = 0 có :
a = –1; b = 2; c = –4 ⇒ a2 + b2 – c = 9 > 0
⇒ phương trình trên là phương trình đường tròn.
+ Phương trình x2 + y2 – 2x – 6y + 20 = 0 có :
a = 1; b = 3; c = 20 ⇒ a2 + b2 – c = –10 < 0
⇒ phương trình trên không là phương trình đường tròn.
+ Phương trình x2 + y2 + 6x + 2y + 10 = 0 có :
a = –3; b = –1; c = 10 ⇒ a2 + b2 – c = 0 = 0
⇒ phương trình trên không là phương trình đường tròn.
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
5
−
2
x
2
+
4
x
−
10
8
;
b)
x
2
+
2
x
+
3
x
2...
Đọc tiếp
Giải các phương trình sau:
a) 5 − 2 x 2 + 4 x − 10 = 8 ;
b) x 2 + 2 x + 3 x 2 + 2 x + 1 = 3 ;
c) x x − 1 x 2 − x + 1 − 6 = 0 .
1.giải hệ phương trình [2x+1\x+1+3y\y-1=1] [3x\x+1-4y-y-1=10].2.Cho phương trình ẩn:x2+mx-2m-4=0,a:giải phương trình khi m=2,bTìm giá trị của tham số m để phương trình có hai nghiệm phân biệt x1,x2 thỏa mãn x1[1-x2]+x2[1-x1]
1:
\(\left\{{}\begin{matrix}\dfrac{2x+1}{x+1}+\dfrac{3y}{y-1}=1\\\dfrac{3x}{x+1}-\dfrac{4y}{y-1}=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2-\dfrac{1}{x+1}+3+\dfrac{3}{y-1}=1\\3-\dfrac{3}{x+1}-\dfrac{4y-4+4}{y-1}=10\end{matrix}\right.\)
=>-1/(x+1)+3/(y-1)=1-2-3=-5 và -3/(x+1)-4/(y-1)=10-3-4=3
=>x+1=13/11 và y-1=-13/18
=>x=2/11 và y=5/18
Đúng 0
Bình luận (0)
Câu 1: Cho phương trình: : x2 – 2mx - 10 = 0
a) Giải phương trình khi m = 1
b) Tìm giá trị của tham số m để phương trình x2 – 2mx + 10 = 0 có hai nghiệm phân
biệt \(x1\), \(x2\) thỏa mãn \(x1^2\) + \(x2^2\) = 29
a) Khi \(m=1\) thì pt đã cho trở thành \(x^2-2x-10=0\) (*)
pt (*) có \(\Delta'=\left(-1\right)^2-\left(-10\right)=11>0\)
Do đó (*) có 2 nghiệm phân biệt \(\left[{}\begin{matrix}x_1=\dfrac{-\left(-1\right)+\sqrt{11}}{1}=1+\sqrt{11}\\x_2=\dfrac{-\left(-1\right)-\sqrt{11}}{1}=1-\sqrt{11}\end{matrix}\right.\)
b) Xét pt đã cho \(x^2-mx-10=0\) \(\left(a=1;b=-m;c=-10\right)\)
Nhận thấy \(ac=1\left(-10\right)=-10< 0\) nên pt đã cho luôn có 2 nghiệm phân biệt \(x_1,x_2\).
Áp dụng hệ thức Vi-ét, ta có \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{-m}{1}=m\\x_1x_2=\dfrac{-10}{1}=-10\end{matrix}\right.\)
Ta có \(x_1^2+x_2^2=29\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=29\Leftrightarrow m^2-2\left(-10\right)=29\)\(\Leftrightarrow m^2+20=29\Leftrightarrow m^2=9\Leftrightarrow m=\pm3\)
Vậy để pt đã cho có 2 nghiệm phân biệt thỏa mãn đề bài thì \(m=\pm3\)
Đúng 2
Bình luận (0)
Giải các phương trình sau:a)
2
x
+
5
6
−
1
3
2
x
+
5
x
−
10
0
;
b)
4
x
−
1...
Đọc tiếp
Giải các phương trình sau:
a) 2 x + 5 6 − 1 3 2 x + 5 x − 10 = 0 ;
b) 4 x − 1 x + 5 = x 2 − 25 ;
c) 3 x − 3 2 − x − 3 x + 2 4 = 0 ;
d) x x + 3 3 − x 4 x + 3 = 0 .