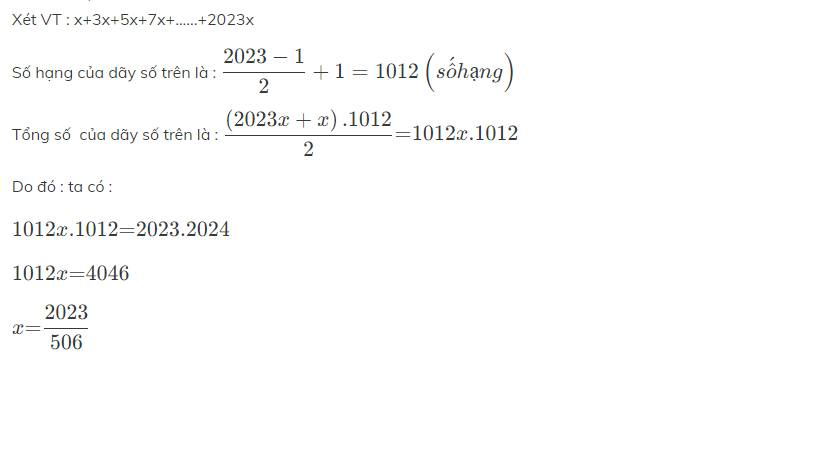`@` `\text {Ans}`

`\downarrow`

`(-2023) \times 33+2023 \times (-68)+2023`

`= 2023 \times (-33 - 68 + 1)`

`= 2023 \times (-101 + 1)`

`= 2023 \times (-100)`

`= -202300`

(-2023) x 33 + 2023 x (-68) + 2023

= 2023 x [(-33) + (-68) + 1]

= 2023 x (-100)

= -202300

Có `xyz=2023=>2023=xyz` 

Thay vào ta có :

\(\dfrac{xyz\cdot x}{xy+xyz\cdot x+xyz}+\dfrac{y}{yz+y+xyz}+\dfrac{z}{xz+z+1}=1\\ \dfrac{x^2yz}{xy\left(1+xz+z\right)}+\dfrac{y}{y\left(z+1+xz\right)}+\dfrac{z}{xz+z+1}=1\\ \dfrac{xz}{1+xz+z}+\dfrac{1}{z+1+xz}+\dfrac{z}{xz+z+1}=1\\ \dfrac{xz+1+z}{1+xz+z}=1\left(dpcm\right)\)

Bạn nhìn tạm nha.

Xét VT : x+3x+5x+7x+......+2023x

Số hạng của dãy số trên là : \(\dfrac{2023-1}{2}+1=1012\left(sốhạng\right)\)

Tổng số  của dãy số trên là : \(\dfrac{\left(2023x+x\right).1012}{2}\text{=}1012x.1012\)

Do đó : ta có :

\(1012x.1012\text{=}2023.2024\)

\(1012x\text{=}4046\)

\(x\text{=}\dfrac{2023}{506}\)

VT = x + 3x + 5x + 7x +... + 2023x = [(2023 - 1):2 +1] . (2023+1)x = 1012. 2024x = 2048288x

VP= 2023 . 2024= 4094552

VT=VP <=> 2048288x =4094552

<=>\(x\approx2\)

`1/2023xx1/5+1/2023xx8/5-1/2023xx16/20`

`=1/2023xx(1/5+8/5-16/20)`

`=1/2023xx(1/5+8/5-4/5)`

`=1/2023xx5/5=1/2023`

TH1: \(x+y+z+t=0\)

\(P=\left(1+\dfrac{x+y}{z+t}\right)^{2023}+\left(1+\dfrac{y+z}{x+t}\right)^{2023}+\left(1+\dfrac{z+t}{x+y}\right)^{2023}+\left(1+\dfrac{t+x}{y+z}\right)^{2023}\)

\(=\left(\dfrac{x+y+z+t}{z+t}\right)^{2023}+\left(\dfrac{x+y+z+t}{x+t}\right)^{2023}+\left(\dfrac{x+y+z+t}{x+y}\right)^{2023}+\left(\dfrac{x+y+z+t}{y+z}\right)^{2023}\)

\(=0+0+0+0=0\) là số nguyên (thỏa mãn)

TH2: \(x+y+z+t\ne0\), áp dụng t/c dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{2023x+y+z+t}=\dfrac{y}{x+2023y+z+t}=\dfrac{z}{x+y+2023z+t}+\dfrac{t}{x+y+z+2023t}\)

\(=\dfrac{x+y+z+t}{\left(2023x+y+z+t\right)+\left(x+2023y+z+t\right)+\left(x+y+2023z+t\right)+\left(x+y+z+2023t\right)}\)

\(=\dfrac{x+y+z+t}{2026\left(x+y+z+t\right)}=\dfrac{1}{2026}\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{2023x+y+z+t}=\dfrac{1}{2026}\\\dfrac{y}{x+2023y+z+t}=\dfrac{1}{2026}\\\dfrac{z}{x+y+2023z+t}=\dfrac{1}{2026}\\\dfrac{t}{x+y+z+2023t}=\dfrac{1}{2026}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}2026x=2023x+y+z+t\\2026y=x+2023y+z+t\\2026z=x+y+2023z+t\\2026t=x+y+z+2023t\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}4x=x+y+z+t\\4y=x+y+z+t\\4z=x+y+z+t\\4t=x+y+z+t\end{matrix}\right.\)

\(\Rightarrow4x=4y=4z=4t\) (vì đều bằng \(x+y+z+t\))

\(\Rightarrow x=y=z=t\)

Do đó:

\(P=\left(1+\dfrac{x+x}{x+x}\right)^{2023}+\left(1+\dfrac{x+x}{x+x}\right)^{2023}+\left(1+\dfrac{x+x}{x+x}\right)^{2023}+\left(1+\dfrac{x+x}{x+x}\right)^{2023}\)

\(=2^{2023}+2^{2023}+2^{2023}+2^{2023}\)

\(=4.2^{2023}=2^{2025}\in Z\)

Em kiểm tra lại đề, 2 ngoặc cuối bị giống nhau, chắc em ghi nhầm

Chứng minh biểu thức thế nào em?

a: \(\left(-2023\right)\cdot33+2023\left(-68\right)+2023\)

\(=2023\left(-33-68+1\right)\)

\(=2023\left(-100\right)=-202300\)

b: \(\left(38-29+43\right)-\left(43+38\right)\)

\(=38-29+43-43-38\)

=(38-38)+(43-43)-29

=0+0-29

=-29

a) (-2023).33+2023.(-68)+2023=2023.(-33)+2023.(-68)+2023

=2023.[(-33)+(-68)+1]

=2023.-100

=-202300