So sánh các cạnh của tam giác ABC a,

Những câu hỏi liên quan
Bài toán 1: Cho tam giác ABC, biết a) So sánh các cạnh của tam giácb) Tia phân giác của góc A cắt BC ở D. So sánh độ dài các đoạn BD và CD.Bài toán 2: Cho tam giác ABC cân ở A có chu vi bằng 16cm, cạnh đáy BC 4cm. So sánh các góc của tam giác ABC.Bài toán 3: Cho tam giác ABC, biết So sánh các cạnh của tam giác.Bài toán 4: Cho tam giác ABC, góc A là góc tù. Trên cạnh AC lấy hai điểm D và E (D nằm giữa A và E). Chứng minh rằng Bài toán 5: Cho tam giác ABC CÓ a) So sánh độ dài các cạ...
Đọc tiếp
Bài toán 1: Cho tam giác ABC, biết ![]()
![]()
a) So sánh các cạnh của tam giác
b) Tia phân giác của góc A cắt BC ở D. So sánh độ dài các đoạn BD và CD.
Bài toán 2: Cho tam giác ABC cân ở A có chu vi bằng 16cm, cạnh đáy BC = 4cm. So sánh các góc của tam giác ABC.
Bài toán 3: Cho tam giác ABC, biết ![]() So sánh các cạnh của tam giác.
So sánh các cạnh của tam giác.
Bài toán 4: Cho tam giác ABC, góc A là góc tù. Trên cạnh AC lấy hai điểm D và E (D nằm giữa A và E). Chứng minh rằng ![]()
Bài toán 5: Cho tam giác ABC CÓ ![]()
a) So sánh độ dài các cạnh AB và AC
b) Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho ![]() Chứng minh
Chứng minh ![]() .
.
Bài toán 6: Tam giác ABC có ![]() Tia phân giác của góc A cắt BC ở D. Chứng minh rằng điểm D nằm giữa hai điểm B và m (M là trung điểm của BC).
Tia phân giác của góc A cắt BC ở D. Chứng minh rằng điểm D nằm giữa hai điểm B và m (M là trung điểm của BC).
Bài toán 7: Tam giác ABC cân tại A. Kẻ tia Bx nằm giữa hai tia BA và BC. Trên tia Bx lấy điểm D nằm ngoài tam giác ABC. Chứng minh rằng ![]()
Bài toán 8: Cho tam giác ABC cân ở A, kẻ ![]() Trên các đoạn thẳng HD và HC, lấy các điểm D và E sao cho
Trên các đoạn thẳng HD và HC, lấy các điểm D và E sao cho ![]() So sánh độ dài AD, AE bằng cách xét hai hình chiếu.
So sánh độ dài AD, AE bằng cách xét hai hình chiếu.
Bài toán 9: Cho tam giác ABC có ![]() và
và ![]() là các góc nhọn. Gọi D là điểm bất kfi thuộc cnahj BC, gọi H và K là chân các đường vuông góc kẻ từ B và C đến đường thẳng AD.
là các góc nhọn. Gọi D là điểm bất kfi thuộc cnahj BC, gọi H và K là chân các đường vuông góc kẻ từ B và C đến đường thẳng AD.
a) So sánh các độ dài BH và BD. Có khi nào BH bằng BD không?
b) So sánh tổng độ dài BH + CK với BC.
Bài toán 10: Cho tam giác ABC cân ở A. Trên cạnh BC lấy điểm D và E sao cho ![]() Gọi M là trung điểm của DE.
Gọi M là trung điểm của DE.
a) Chứng minh rằng ![]()
b) So sánh độ dài AB, AD, AE, AC.
Bài toán 11: Cho tam giác ABC ![]() Gọi M là một điểm nằm giữa B và C. Gọi E và F là hình chiếu của B và C xuống đường thẳng AM. So sánh tổng
Gọi M là một điểm nằm giữa B và C. Gọi E và F là hình chiếu của B và C xuống đường thẳng AM. So sánh tổng ![]() với BC
với BC
Bài toán 2: Cho tam giác ABC cân ở A có chu vi bằng 16cm, cạnh đáy BC = 4cm. So sánh các góc của tam giác ABC.
Tam giác ABC cân tại A (gt). => Góc B = Góc C (Tính chất tam giác cân).
Ta có: Tam giác ABC cân ở A có chu vi bằng 16cm, cạnh đáy BC = 4cm (gt).
=> AB = AC = (16 - 4) : 2 = 6 (cm).
Xét tam giác ABC cân tại A:
Ta có: AB > BC (AB = 6 cm; BC = 4cm).
=> Góc C > Góc A.
Vậy trong tam giác ABC có Góc B = Góc C > Góc A.
Đúng 1
Bình luận (0)
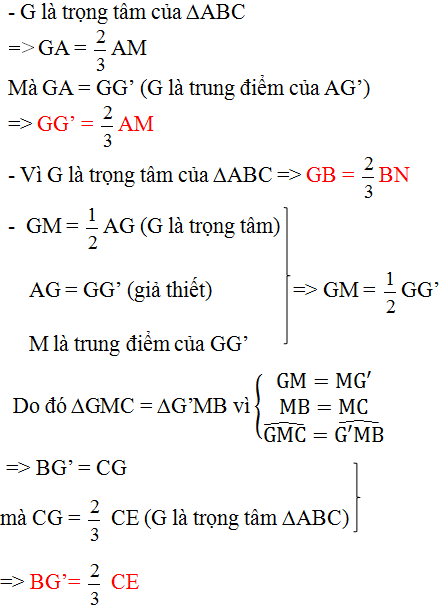
Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'.
a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC
b) So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC
Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'.
a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC.
b) So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC.
Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy G" sao cho G là trung điểm của AG".
a) So sánh các cạnh của tam giác BGG" vói các đường trung tuyến của tam giác ABC
b) So sánh các đường trung tuyến của tam giác BGG" với các cạnh của tam giác ABC
Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'
a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC
b) So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC
Hướng dẫn:
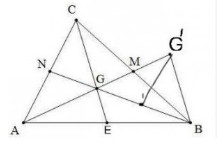
a) So sánh các cạnh của ∆BGG’ với các đường trung tuyến của ∆ABC BG cắt AC tại N
CG cắt AB tại E
G là trọng tâm của ∆ABC
=> GA =  AM
AM
Mà GA = GG’ ( G là trung điểm của AG ‘)
GG’ =  AM
AM
Vì G là trọng tâm của ∆ABC => GB =  BN
BN
Mặt khác : GM =  AG ( G là trọng tâm )
AG ( G là trọng tâm )
AG = GG’ (gt)
GM =  GG’
GG’
M là trung điểm GG’
Do đó ∆GMC = ∆G’MB vì :
GM = MG’
MB = MC
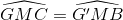
=> BG' = CG
mà CG =  CE (G là trọng tâm ∆ABC)
CE (G là trọng tâm ∆ABC)
=> BG' =  CE
CE
Vậy mỗi cạnh của ∆BGG' bằng  đường trung tuyến của ∆ABC
đường trung tuyến của ∆ABC
b) So sánh các đường trung tuyến của ∆BGG' với cạnh ∆ABC
ta có: BM là đường trung tuyến ∆BGG'
mà M là trung điểm của BC nên BM =  BC
BC
Vì IG =  BG (I là trung điểm BG)
BG (I là trung điểm BG)
GN =  BG ( G là trọng tâm)
BG ( G là trọng tâm)
=> IG = GN
Do đó ∆IGG' = ∆NGA (cgc) => IG' = AN => IG' = 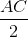
- Gọi K là trung điểm BG => GK là trung tuyến ∆BGG'
Vì GE =  GC (G là trọng tâm ∆ABC)
GC (G là trọng tâm ∆ABC)
=> GE =  BG
BG
mà K là trung điểm BG' => KG' = EG
Vì ∆GMC = ∆G'BM (chứng minh trên)
=> 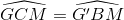 (lại góc sole trong)
(lại góc sole trong)
=> CE // BG' => 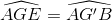 (đồng vị)
(đồng vị)
Do đó ∆AGE = ∆GG'K (cgc) => AE = GK
mà AE =  AB nên GK =
AB nên GK =  AB
AB
Vậy mỗi đường trung tuyến ∆BGG' bằng một nửa cạnh của tam giác ABC song song với nó
Đúng 0
Bình luận (0)
Hướng dẫn làm bài:
a)So sánh các cạnh của ∆BGG’ với các đường trung tuyến của ∆ABC
BG cắt AC tại N
CG cắt AB tại E
G là trọng tâm của ∆ABC
=> GA=23AMGA=23AM
Mà GA = GG’ (G là trung điểm của AG’)
=> GG′=23AMGG′=23AM
Vì G là trọng tâm của ∆ABC => GB=23BNGB=23BN
Mặt khác :
M là trung điểm GM=12AG(TT)AG=GG′(Gt)}=>GM=12GG′GM=12AG(TT)AG=GG′(Gt)}=>GM=12GG′
Do đó ∆GMC=∆G’MB vì ⎧⎪⎨⎪⎩GM=MG′MB=MCˆGMC=ˆG′MB{GM=MG′MB=MCGMC^=G′MB^
=> BG′=CGCG=23CEBG′=CGCG=23CE (G là trọng tâm tam giác ABC)
=>BG′=23CE=>BG′=23CE
Vậy mỗi cạnh của ∆BGG’ bằng 2323 đường trung tuyến của ∆ABC
b)So sánh các đường trung tuyến của ∆BGG’ với cạnh ∆ABC.
-Ta có: BM là đường trung tuyến ∆BGG’
Mà M là trung điểm của BC nên BM=12BCBM=12BC
Vì IG=12BGIG=12BG (Vì I là trung điểm BG)
GN=12BGGN=12BG (G là trọng tâm)
=> IG = GN
Do đó ∆IGG’=∆NGA (c.g.c) => IG′=AN=>IG′=AC2IG′=AN=>IG′=AC2
-Gọi K là trung điểm BG => GK là trung điểm ∆BGG’
Vì GE=12GCGE=12GC (G là trọng tâm tam giác ABC)
BG' = GC (Chứng minh trên)
=>GE=12BG=>GE=12BG
Mà K là trung điểm BG’ =>KG’ = EG
Vì ∆GMC = ∆G’MB (chứng minh trên)
=> ˆGCM=ˆG′BMGCM^=G′BM^ (So le trong)
=>CE // BG’ => ˆAGE=ˆAG′BAGE^=AG′B^ (đồng vị)
Do đó ∆AGE = ∆GG’K (c.g.c) =>AE = GK
Mà AE=12AB⇒GK=12AB
Đúng 0
Bình luận (0)
Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'.
a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC.
b) So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC
Bài giải
a) Gọi M, N, E lần lượt là trung điểm của AB, BC, CA.
Vậy mỗi cạnh của ΔBGG' bằng 2/3 đường trung tuyến của ΔABC.
b) Gọi I, K lần lượt là trung điểm của BG và BG'.
 Vậy mỗi đường trung tuyến của ΔBGG' bằng một nửa cạnh của ΔABC tương ứng với nó.~Hok tốt~
Vậy mỗi đường trung tuyến của ΔBGG' bằng một nửa cạnh của ΔABC tương ứng với nó.~Hok tốt~
Đúng 1
Bình luận (0)
Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'
a) So sánh các cạnh tam giác BGG' với các đường trung tuyến cả tam giác ABC
b) So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC
Cho tam giác ABC có góc ngoài tại đỉnh A là 120 độ , góc B bằng 70 ,độ kẻ phân giác BE
a ,Tính góc AEB
b, so sánh các cạnh của tam giác ABE
c, So sánh các cạnh của tam giác Bec
a: góc BAC=180-120=60 độ
góc ABE=70/2=35 độ
góc AEB=180-60-35=85 độ
b: góc ABE<góc BAE<góc AEB
=>AE<BE<AB
c: góc ECB=180-70-60=50 độ
góc BEC=180-85=95 độ
Vì góc EBC<góc ECB<góc BEC
nên EC<EB<BC
Đúng 1
Bình luận (0)
gọi G là trọng tâm Của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG
a, So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC
b, So sánh các đường trung tuyến của tam giác BGG' với cạnh của tam giác ABC
Cho tam giác ABC, M là trung điểm của BC. Trên tia AM lấy điểm D sao cho trọng tâm G là trung điểm AD.
a, So sánh các cạnh GD và cạnh BD của tam giác BGD với các đường trung tuyến của tam giác ABC
b, So sánh các đường trung tuyến của tam giác BGD với các cạnh AB và AC của tam giác ABC