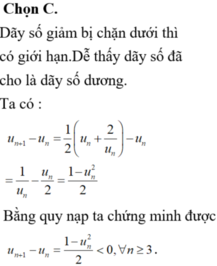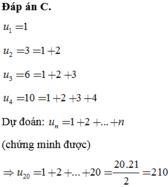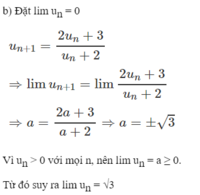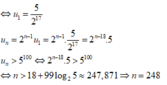Cho (Un) với U1=1 Un+1= 2Un - 2 Tìm Un

Những câu hỏi liên quan
Cho dãy số
u
n
được xác định bởi
u
1
1
;
u
n
+
1
1
2
u
n
+
2
u
n...
Đọc tiếp
Cho dãy số u n được xác định bởi u 1 = 1 ; u n + 1 = 1 2 u n + 2 u n với mọi n ≥ 1 . Tìm lim u n
A. 1
B. -1
C. 2
D. - 2
Cho dãy số
u
n
được xác định bởi
u
1
1
,
u
n
+
1
1
2
u
n
+
2
u
n...
Đọc tiếp
Cho dãy số u n được xác định bởi u 1 = 1 , u n + 1 = 1 2 u n + 2 u n với mọi n ≥ 1 . Tìm giới hạn của u n
A. l i m u n = 1
B. l i m u n = - 1
C. l i m u n = 2
D. l i m u n = - 2
Chọn C.
Phương pháp : Dãy số giảm bị chặn dưới thì có giới hạn.
Cách giải : Dễ thấy dãy số đã cho là dãy số dương.
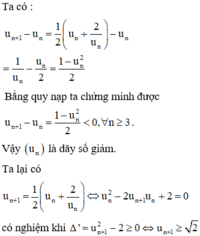
Vậy dãy số đã cho giảm và bị chặn dưới nên có giới hạn.
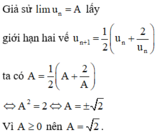
Đúng 0
Bình luận (0)
Cho U1=2015,Un+1=Un/Un+2 tính U21 b)U1=2015;Un+1=2Un+5.Tính A= U10+5U12+U20/U5
Cho dãy số
(
u
n
)
u
1
1
;
u
2
...
Đọc tiếp
Cho dãy số ( u n ) u 1 = 1 ; u 2 = 2 u n + 1 = 2 u n - u n - 1 + 1 v ớ i n ≥ 2
a) Viết năm số hạng đầu của dãy số;
b) Lập dãy số ( v n ) với v n = u n + 1 − u n . Chứng minh dãy số (vn) là cấp số cộng;
Cho dãy
u
n
với
u
1
1
,
u
2
3
u
n...
Đọc tiếp
Cho dãy u n với u 1 = 1 , u 2 = 3 u n + 2 = 2 u n + 1 − u n + 1 với n ∈ ℕ * . Tính u 20
A. 190
B. 420
C. 210
D. -210
Cho dãy
u
n
với
u
1
1
,
u
2
3
u
n
+
2...
Đọc tiếp
Cho dãy u n với u 1 = 1 , u 2 = 3 u n + 2 = 2 u n + 1 - u n + 1 với n ∈ N * . Tính u 20 .
A. u 20 = 190
B. u 20 = 420
C. u 20 = 210
D. u 20 = - 210
Đáp án C.
u 1 = 1
u 2 = 3 = 1 + 2
u
3
=
6
=
1
+
2
+
3
u
4
=
10
=
1
+
2
+
3
+
4
Dự đoán: u n = 1 + 2 + . . . + n (chứng minh được)
⇒ u 20 = 1 + 2 + . . . + 20 = 20 . 21 2 = 210
Cách 2: CASIO
Ghi và màn hình x = x + 1 : C = 2 B - A + 1 : A = B : B = C
Bấm CALC gán x = 2;B = 3;A = 1
Lặp lại phím = cho đến khi x = x + 1 = 20 ta được
⇒ u 20 = C = 2 B - A + 1 = 210
Đúng 0
Bình luận (0)
Cho dãy số
(
u
n
)
xác định bởi
u
1
1
u
n
+
1...
Đọc tiếp
Cho dãy số ( u n ) xác định bởi u 1 = 1 u n + 1 = 2 u n + 3 u n + 2 v ớ i n ≥ 1
a) Chứng minh rằng u n > 0 với mọi n.
b) Biết ( u n ) có giới hạn hữu hạn. Tìm giới hạn đó.
Cho dãy số
(
u
n
)
thỏa mãn
log
u
1
+
2
+
log
u
1
-
2
log
u
10
2
log
u...
Đọc tiếp
Cho dãy số ( u n ) thỏa mãn log u 1 + 2 + log u 1 - 2 log u 10 = 2 log u 10
và u n + 1 = 2 u n với mọi n ≥ 1 Giá trị nhỏ nhất của n đề u n > 5 100 bằng
A. 247
B. 248
C. 229
D. 290
Cho dãy số (un) thỏa mãn
log
u
1
+
2
+
log
u
1
-
2
log
u
10
2
log
u
10...
Đọc tiếp
Cho dãy số (un) thỏa mãn log u 1 + 2 + log u 1 - 2 log u 10 = 2 log u 10 và un+1 = 2un với mọi n ≥ 1 . Giá trị nhỏ nhất của n để un > 5100 bằng
A. 247.
B. 248.
C. 229.
D. 290.
Đáp án B.
Đặt t = 2 + log u 1 - 2 log u 10 ≥ 0
⇔ 2 log u 1 - 2 log u 10 = t 2 - 2 ,
khi đó giả thiết trở thành:
log u 1 - 2 log u 10 + 2 + log u 1 - 2 log u 10 = 0
⇔ t 2 + t - 2 = 0
<=> t = 1 hoặc t = -2
⇒ log u 1 - 2 log u 10 = - 1
⇔ log u 1 + 1 = 2 log u 10
⇔ log 10 u 1 = log u 10 2 ⇔ 10 u 1 = u 10 2 ( 1 )
Mà un+1 = 2un => un là cấp số nhân với công bội q = 2
=> u10 = 29 u1 (2)
Từ (1), (2) suy ra
10 u 1 = 9 9 u 1 2 ⇔ 2 18 u 1 2 = 10 u 1 ⇔ u 1 = 10 2 18
⇒ u n = 2 n - 1 . 10 2 18 = 2 n . 10 2 19 .
Do đó u n > 5 100 ⇔ 2 n . 10 2 19 > 5 100
⇔ n > log 2 5 100 . 2 19 10 = - log 2 10 + 100 log 2 5 + 19 ≈ 247 , 87
Vậy giá trị n nhỏ nhất thỏa mãn là n = 248.
Đúng 0
Bình luận (0)