d1: x-3y+1=0 và d2: x-2y-5=0 tìm số đo giữa hai đường thẳng và toạ độ giao điểm

Những câu hỏi liên quan
Tìm số đo của góc giữa hai đường thẳng d1 và d2 lần lượt có phương trình: d1: 4x – 2y + 6 = 0 và d2: x – 3y + 1 = 0
Với d1: 4x – 2y + 6 = 0 có vecto pháp tuyến là: n1→(4;-2)
và d2: x – 3y + 1 = 0 có vecto pháp tuyến là: n2→(1;-3) ; ta có :
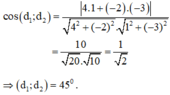
Đúng 2
Bình luận (0)
Vẽ hai đường thẳng: (
d
1
): x + y 2 và (
d
2
): 2x + 3y 0. Hỏi đường thẳng (
d
3
): 3x + 2y 10 có đi qua giao điểm của (
d
1
) và (
d
2
) hay không?
Đọc tiếp
Vẽ hai đường thẳng: ( d 1 ): x + y = 2 và ( d 2 ): 2x + 3y = 0. Hỏi đường thẳng ( d 3 ): 3x + 2y = 10 có đi qua giao điểm của ( d 1 ) và ( d 2 ) hay không?
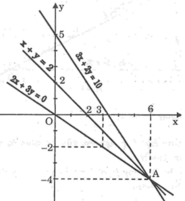
Vẽ đường thẳng ( d 1 ) là đồ thị hàm số y = -x + 2
Cho x = 0 thì y = 2 ⇒ (0; 2)
Cho y = 0 thì x = 2 ⇒ (2; 0)
Vẽ đường thẳng (
d
2
) là đồ thị hàm số 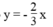
Cho x = 0 thì y = 0 ⇒ (0; 0)
Cho x = 3 thì y = -2 ⇒ (3; -2)
Hai đường thẳng ( d 1 ) và ( d 2 ) cắt nhau tại A(6; -4). Thay các giá trị x và y này vào phương trình đường thẳng ( d 3 ), ta có:
3.6 + 2.(-4) = 18 – 8 = 10.
Vậy x và y thỏa phương trình 3x + 2y = 10 nên (x; y) = (6; -4) là nghiệm của phương trình 3x + 2y = 10.
Đúng 0
Bình luận (0)
Lập phương trình của đường thẳng ∆ đi qua giao điểm của hai đường thẳng d1: x + 3y – 1 =0 d2: x – 3y - 5= 0 và vuông góc với đường thẳng d3: 2x - y + 7 = 0.
A. 3x + 6y - 5=0.
B. 6x + 12y - 5 = 0.
C. 6x+ 12y + 10 = 0.
D. x +2y + 10 = 0.
Trong mặt phẳng 0xy , cho 3 đường thẳng d1 : x+2y+1=0 ; d2 : x+y-5=0 và d3 : 2x+3y-10=0 . Phương trình đường thẳng delta đi qua giao điểm của d1d2 và song song với d3 là
Giao điểm A của d1 và d2 là nghiệm:
\(\left\{{}\begin{matrix}x+2y+1=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=11\\y=-6\end{matrix}\right.\)
\(\Delta\) song song d3 nên nhận (2;3) là 1 vtpt, nên có pt:
\(2\left(x-11\right)+3\left(y+6\right)=0\Leftrightarrow2x+3y-4=0\)
Đúng 1
Bình luận (0)
Giao điểm của hai đường thẳng
d
1
:
x
+
2
y
1
và
d
2
:
2
x
+
3
y
-
5
là: A.
13
;
7
B.
13
;
-...
Đọc tiếp
Giao điểm của hai đường thẳng d 1 : x + 2 y = 1 và d 2 : 2 x + 3 y = - 5 là:
A. 13 ; 7
B. 13 ; - 7
C. - 13 ; 7
D. - 13 ; - 7
Giao điểm của hai đường thẳng d1 và d2 là nghiệm hệ phương trình:
x + 2 y = 1 2 x + 3 y = - 5
Ta tính các định thức:
D = 1 2 2 3 = 1 . 3 - 2 . 2 = - 1 ; D x = 1 2 - 5 3 = 1 . 3 - ( - 5 ) . 2 = 13 D y = 1 1 2 - 5 = 1 . ( - 5 ) - 2 . 1 = - 7
Suy ra: x = D x D = - 13 ; y = D y D = 7
Do đó hai đường thẳng đã cho cắt nhau tại điểm (-13; 7).
Đúng 0
Bình luận (0)
Cho hai đường thẳng: (d1):y=1/2x+2 và (d2):y=-x+2
a) vẽ (d1) và (d2) trên cùng một hệ trục toạ độ Oxy
b) gọi A là giao điểm của (d1) với trục hoành. Tìm toạ độ điểm A
c) gọi B là giao điểm của (d2) với trục tung. Tìm toạ đồ điểm B
d)gọi C là giao điểm của (d1) và (d2). Tìm toạ độ điểm C
Mông các bạn giải giúp mình gấp với ạ :3
a/ bạn tự làm
b/ \(\Rightarrow y=0\Rightarrow\dfrac{1}{2}x+2=0\) giải PT tìm hoành độ x
c/ \(\Rightarrow x=0\Rightarrow y=0+2=2\)
d/ \(\Rightarrow\dfrac{1}{2}x+2=-x+2\) Giải PT tìm hoành độ x của C rồi thay vào d1 hoặc d2 để tìm tung độ y của C
Đúng 0
Bình luận (0)
Tìm a và b biết đường thẳng y = ax + b đi qua hai điểm A(2;-1) và B (1;-3) b tìm toạ độ giao điểm của hai đường thẳng (d1) 2x+y=-3 và (d2) 3x-2y=-1
a: Theo đề, ta có hệ:
2a+b=-1 và a+b=-3
=>a=2 và b=-5
b; tọa độ giao là:
2x+y=-3 và 3x-2y=-1
=>x=-1 và y=-1
Đúng 0
Bình luận (0)
Cho dduongf thẳng d1: y=4x-3 vf dduongf thẳng d2: y=-x+2
Tìm toạ độ giao điểm của đường thẳngd1 và d2( = phép tính 0 cần vẽ)
| x | 0 | 1 |
| y=4x−3 | −3 | 1 |
| x | 0 | 1 |
| y=−x+2 | 2 | 1 |
Ta có phương trình hoàng độ giao điểm:
4x−3=−x+2
⇔5x=5
⇔x=1
⇒y=−x+2=−1+2=1
Vậy 2 đồ thị cắt nhau tại A(1;1)
Đúng 0
Bình luận (0)
| \(x\) | \(0\) | \(1\) |
| \(y=4x-3\) | \(-3\) | \(1\) |
| \(x\) | \(0\) | \(1\) |
| \(y=-x+2\) | \(2\) | \(1\) |
Ta có phương trình hoàng độ giao điểm:
\(4x-3=-x+2\)
\(\Leftrightarrow5x=5\)
\(\Leftrightarrow x=1\)
\(\Rightarrow y=-x+2=-1+2=1\)
Vậy 2 đồ thị cắt nhau tại \(A\left(1;1\right)\)
Đúng 0
Bình luận (0)
Cho 2 đường thẳng (d1) y=3x + 4 và (d2) x - 2y =0 một điểm A ( -1; 1)
a xét vị trí tương đối của A với 2 đường thẳng
b tìm giao điểm (d1) và ( d2)
c tìm m để (d3) : ( m-1)x + (m-2)y + m +1=0 đồng quy với (d1) và (d2)
a) Thay hoành độ và tung độ của A vào 2 pt đường thẳng (d1) và (d2), ta lần lượt được:
\(1=3\left(-1\right)+4\) (luôn đúng)
\(-1-2.1=0\) (vô lí)
Như vậy, \(A\in d_1;A\notin d_2\)
b) Gọi giao điểm của d1, d2 là \(B\left(x_0;y_0\right)\). Khi đó \(x_0,y_0\) là các số thỏa mãn \(\left\{{}\begin{matrix}y_0=3x_0+4\\x_0-2y_0=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y_0=6y_0+4\\x_0=2y_0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y_0=-\dfrac{4}{5}\\x_0=-\dfrac{8}{5}\end{matrix}\right.\)
Vậy giao điểm của d1 và d2 là \(B\left(-\dfrac{8}{5};-\dfrac{4}{5}\right)\)
c) Để đường thẳng d1, d2, d3 đồng quy thì d3 phải đi qua giao điểm của d1 và d2. Nói cách khác, d3 phải đi qua điểm \(B\left(-\dfrac{8}{5};-\dfrac{4}{5}\right)\)
\(\Leftrightarrow\left(m-1\right).\dfrac{-8}{5}+\left(m-2\right).\dfrac{-4}{5}+m+1=0\)
\(\Leftrightarrow\dfrac{21}{5}-\dfrac{7}{5}m=0\)
\(\Leftrightarrow m=3\)
Vậy \(m=3\) thỏa mãn ycbt.
Đúng 1
Bình luận (0)

















