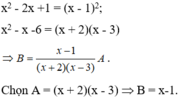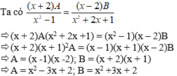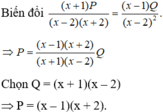Đưa về M = x − 1 ( x + 3 ) 2 N .  Chọn N = ( x   +   3 ) 2  Þ M = x - 1.

\(f\left(x\right)\) chia \(x+1\) dư -15 \(\Rightarrow f\left(-1\right)=-15\Rightarrow-a+b=-16\)

\(f\left(x\right)\) chia \(x-3\) dư 45 \(\Rightarrow f\left(3\right)=45\Rightarrow3a+b=0\)

\(\Rightarrow\left\{{}\begin{matrix}-a+b=-16\\3a+b=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=4\\b=-12\end{matrix}\right.\)

\(f\left(x\right)=x^4-x^3-x^2+4x-12=\left(x^2-4\right)\left(x^2-x+3\right)\)

\(f\left(x\right)=0\Leftrightarrow x^2-4=0\Rightarrow x=\pm2\)

a) Đa thức A là:

\(\dfrac{-2x+4}{x-2}=\dfrac{2}{A}\)

\(\Leftrightarrow\dfrac{-2\left(x-2\right)}{x-2}=\dfrac{2}{A}\)

\(\Leftrightarrow-2=\dfrac{2}{A}\)

\(\Leftrightarrow A=\dfrac{2}{-2}=-1\)

b) Đa thức A là:

\(\dfrac{2x^2+4x}{x+2}=\dfrac{A}{2}\)

\(\Leftrightarrow\dfrac{2x\left(x+2\right)}{x+2}=\dfrac{A}{2}\)

\(\Leftrightarrow2x=\dfrac{A}{2}\)

\(\Leftrightarrow A=2x\cdot2=4x\)

c) Đa thức A là:

\(\dfrac{x-4}{x^2-16}=\dfrac{1}{A}\)

\(\Leftrightarrow\dfrac{x-4}{\left(x+4\right)\left(x-4\right)}=\dfrac{1}{A}\)

\(\Leftrightarrow\dfrac{1}{x+4}=\dfrac{1}{A}\)

\(\Leftrightarrow A=x+4\)

d) Đa thức A là:

\(\dfrac{x^3+8}{x+2}=\dfrac{A}{2}\)

\(\Leftrightarrow\dfrac{\left(x+2\right)\left(x^2+2x+4\right)}{x+2}=\dfrac{A}{2}\)

\(\Leftrightarrow x^2+2x+4=\dfrac{A}{2}\)

\(\Leftrightarrow A=2\cdot\left(x^2+2x+4\right)=2x^2+4x+8\)

Đề ạ   

a: 2/A=-2x+4/x-2

=>2/A=-2

=>A=-1

b: 2x^2+4x/x+2=A/2

=>A/2=2x

=>A=4x

c: (x-4)/(x^2-16)=1/A

=>1/A=1/x+4

=>A=x+4

d: (x^3+8)/(x+2)=A/2

=>A/2=x^2-2x+4

=>A=2x^2-4x+8

1. Để tìm các đa thức P(x) thỏa mãn điều kiện P(2014) = 2046 và P(x) = P(x^2 + 1) - 33 + 32, ∀x ≥ 0, ta có thể sử dụng phương pháp đệ quy. Bước 1: Xác định bậc của đa thức P(x). Vì không có thông tin về bậc của đa thức, chúng ta sẽ giả sử nó là một hằng số n. Bước 2: Xây dựng công thức tổng quát cho đa thức P(x). Với bậc n đã xác định, ta có: P(x) = a_n * x^n + a_{n-1} * x^{n-1} + ... + a_0 Bước 3: Áp dụng điều kiện để tìm các hệ số a_i. Thay x = 2014 vào biểu thức và giải phương trình: P(2014) = a_n * (2014)^n + a_{n-1} * (2014)^{n-1} + ... + a_0 = 2046 Giải phương trình này để tìm các giá trị của các hệ số. Bước 4: Áp dụng công thức tái lập để tính toán các giá trị tiếp theo của P(x): P(x) = P(x^2+1)-33+32 Áp dụng công thức này lặp lại cho đến khi đạt được kết quả cuối cùng. 2. Để tìm các đa thức P(x) ∈ Z[x] bậc n thỏa mãn điều kiện [P(2x)]^2 = 16P(x^2), ∀x ∈ R, ta có thể sử dụng phương pháp đệ quy tương tự như trên. Bước 1: Xác định bậc của đa thức P(x). Giả sử bậc của P(x) là n. Bước 2: Xây dựng công thức tổng quát cho P(x): P(x) = a_n * x^n + a_{n-1} * x^{n-1} + ... + a_0 Bước 3: Áp dụng điều kiện để tìm các hệ số a_i. Thay x = 2x vào biểu thức và giải phương trình: [P(2x)]^2 = (a_n * (2x)^n + a_{n-1} * (2x)^{n-1} + ... + a_0)^2 = 16P(x^2) Giải phương trình này để tìm các giá trị của các hệ số. Bước 4: Áp dụng công thức tái lập để tính toán các giá trị tiếp theo của P(x): [P(4x)]^2 = (a_n * (4x)^n + a_{n-1} * (4x)^{n-1} + ... + a_0)^2 = 16P(x^2) Lặp lại quá trình này cho đến khi đạt được kết quả cuối cùng.