Cho tam giác \(ABC\) vuông tại \(A\), đường trung tuyến \(AM\). Biết \(AB = 8\)cm; \(AC = 15\)cm. Độ dài đoạn \(AM\) là:
A. 8,5cm
B. 8cm
C. 7cm
D. 7,5cm
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường trung tuyến AM,BE,CF. Biết AB=6 cm, AC=8 cm. Tính độ dài các đường trung tuyến trong tam giác ABC
Cho tam giác ABC vuông tại A có AB = 8 cm AC = 6 cm độ dài đường trung tuyến AM bằng
A2,5cm
B10cm
C25cm
5cm
Xem thêm câu trả lời
Bài 1. Cho tam giác ABC cân tại A. Kẻ AM vuông góc với BC tại M
a) Chứng minh AM là trung tuyến của tam giác
b) Biết AB = 15 cm; BC = 12 cm. Tính độ dài đường trung tuyến AM.
Cho tam giác ABC vuông tại A , đường cao AH , trung tuyến AM .Biết AH =4 cm , AM = 4,1 cm . Tỉ số độ dài 2 canh goc vuông AB và AC của tam giác ABC = ?
Cho tam giác ABC vuông tại A có đường cao AH và đường trung tuyến AM .Biết AH = 3cm, HB = 4 cm. Hãy tính AB AC AM , và diện tích tam giác ABC .
Xét tam giác ABH vuông tại H, ta có:
\(AB^2=AH^2+BH^2\)\(=3^2+4^2=25\)
\(\Rightarrow AB=5\left(cm\right)\)
Xét tam giác ABC vuông tại A, theo hệ thức lượng ta có:
\(AH^2=AB\cdot AC\Rightarrow AC=\dfrac{AH^2}{AB}=\dfrac{3^2}{5}=1,8\left(cm\right)\)
Do đó:\(BC=\sqrt{AB^2+AC^2}=\sqrt{5^2+1,8^2}\simeq5,3\left(cm\right)\)
AM là đường trung tuyến trong tam giác vuông ABC
=> AM=\(\dfrac{1}{2}\) BC= 2,65 \(\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Đường trung tuyến AM, vẽ BH vuông góc AM, biết AB 15cm, BH 12cm. Tính BC cm
Cho tam giác ABC vuông tại A. Đường trung tuyến AM, vẽ BH vuông góc AM, biết AB=15cm, BH=12cm. Tính BC=? cm
Xét t.giác ABH vg tại H có:
AB2= BH2 + AH2 (đlí Pytago)
TS: 225= 144+ AH2
=> AH= 9(cm)
Đặt HM= x
ta có : AM2= (x+9)2
AM2 = BM2= 122 +x2
=> (x+9)2= 122 + x2
= x2 + 18x+81= 144+x2
= x2 +18x+81-144+x2=0
18x+81= 144
18x= 163
=>x=3,5
=> HM= 3,5(cm)
ta có AM= AH+HM
t/s: AM= 9+3,5
AM= 12,5
ta có BC= 2AM(t/c)
=> BC= 25
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A, biết AB=3cm; AC=4cm. Kẻ đường cao AH và trung tuyến AM. CM tam giác AHB và tam giác ABC đồng dạng
Xét \(\Delta ABC\&\Delta ABH\) ta có:
\(\widehat{A}=\widehat{B}=90^o\left(gt\right)\\ \widehat{B}=\widehat{B}\\\Rightarrow \Delta ABC\&\sim ABH\)
Đúng 2
Bình luận (2)
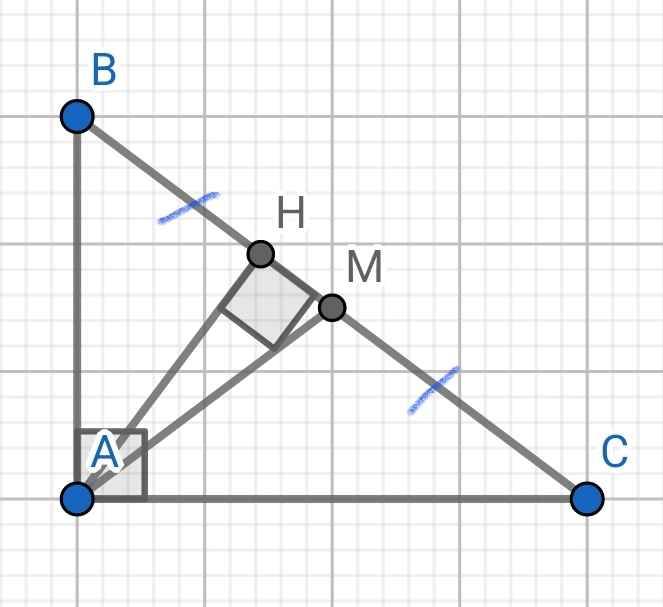
Xét ∆AHB và ∆CBA có:
∠AHB = ∠CAB = 90⁰
∠B chung
⇒ ∆AHB ∽ ∆CBA (g-g)
Đúng 1
Bình luận (0)
Xét ΔABC&ΔABH ta có:
góc A= góc B= 90 độ (gt)
góc B= góc B
⇒ΔABC&∼ABH
Đúng 1
Bình luận (1)
Cho tam giác ABC vuông tại A có đường cao AH và đường trung tuyến AM .Biết AH = 3cm, HB = 4 cm. Hãy tính AB AC AM , và diện tích tam giác ABC .