Tìm tập xác định của các hàm số sau:
\(\begin{array}{l}a)\;y = \frac{1}{{cosx}}\\b)\;y = tan(x + \frac{\pi }{4})\\c)\;y = \frac{1}{{2 - si{n^2}x}}\end{array}\)
Cho hàm số: \(y = \left\{ \begin{array}{l} - x\,{\rm{ nếu} \, x < 0}\\{ x\, \rm{nếu} \, x > 0}\end{array} \right.\)
a) Tìm tập xác định của hàm số trên.
b) Tính giá trị của hàm số khi \(x = - 1;x = 2022\)
a) Tìm tập xác định của hàm số trên.
\(f\left( x \right)\) có nghĩa khi x0.
=> Tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
b) Tính giá trị của hàm số khi \(x = - 1;x = 2022\)
Với \(x = - 1\), suy ta \(x < 0\)\( \Rightarrow y = - x = - \left( { - 1} \right) = 1\).
Với \(x = 2022\), suy ra \(x > 0\)\( \Rightarrow y = x = 2022\).
Tìm tập xác định, tập giá trị và vẽ đồ thị hàm số:
\(f(x) = \left\{ \begin{array}{l} - 1\quad \quad x < 0\\1\;\quad \quad \;{\kern 1pt} x > 0\end{array} \right.\quad \)
Tham khảo:
+) Dễ thấy: hàm số được xác định với mọi \(x > 0\) và \(x < 0\).
Do đó tập xác định của hàm số là \(D = \mathbb{R}{\rm{\backslash }}\{ 0\} \)
+) Với \(x \in D\):
+ Nếu \(x > 0\) thì \(f(x) = 1\)
+ Nếu \(x < 0\) thì \(f(x) = - 1\)
Vậy tập giá trị của hàm số là \(T = \{ - 1;1\} \)
+) Vẽ đồ thị hàm số:
Với \(x \in ( - \infty ;0)\) đồ thị hàm số là đường thẳng \(y = - 1\)
Với \(x \in (0; + \infty )\) đồ thị hàm số là đường thẳng \(y = 1\)
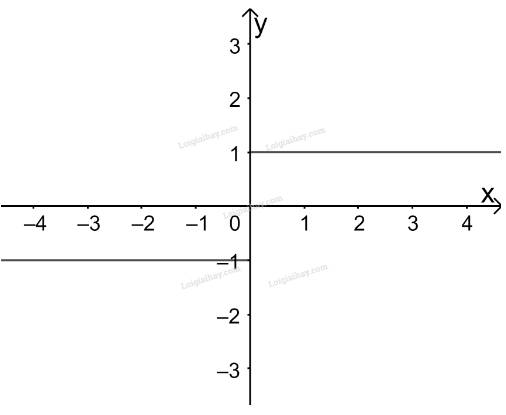
Ta được đồ thị hàm số như hình trên.
Tìm tập xác định của mỗi hàm số sau:
a) \(y = - {x^2}\)
b) \(y = \sqrt {2 - 3x} \)
c) \(y = \frac{4}{{x + 1}}\)
d) \(y = \left\{ \begin{array}{l}1{\rm{ khi }}x \in \mathbb{Q}\\0{\rm{ khi }}x \in \mathbb{R}\backslash \mathbb{Q}\end{array} \right.\)
a) Ta thấy hàm số có nghĩa với mọi số thực nên \(D = \mathbb{R}\)
b)
Điều kiện: \(2 - 3x \ge 0 \Leftrightarrow x \le \frac{2}{3}\)
Vậy tập xác định: \(S = \left( { - \infty ;\frac{2}{3}} \right]\)
c) Điều kiện: \(x + 1 \ne 0 \Leftrightarrow x \ne - 1\)
Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\)
d) Ta thấy hàm số có nghĩa với mọi \(x \in \mathbb{Q}\) và \(x \in \mathbb{R}\backslash \mathbb{Q}\) nên tập xác định: \(D = \mathbb{R}\).
Xác định và so sánh tập nghiệm của các phương trình sau:
\(\begin{array}{l}a)\;x - 1 = 0\\b)\;{x^2} - 1 = 0\\c)\sqrt {2{x^2} - 1} = x\end{array}\)
\(a,x-1=0\Leftrightarrow x=1\)
Vậy tập nghiệm của phương trình là \(S=\left\{1\right\}\)
\(b,x^2-1=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy tập nghiệm của phương trình là \(S=\left\{-1;1\right\}\)
c, ĐK: \(x\ge\dfrac{\sqrt{2}}{2}\)
\(\sqrt{2x^2-1}=x\Leftrightarrow2x^2-1=x^2\Leftrightarrow x^2=1\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy tập nghiệm của phương trình là \(S=\left\{-1;1\right\}\)
Từ đó, hai phương trình b và c có cùng tập nghiệm.
Hãy xác định đúng đồ thị của mỗi hàm số sau trên Hình 12.
\(\begin{array}{l}({P_1}):y = - 2{x^2} - 4x + 2;\\({P_2}):y = 3{x^2} - 6x + 5;\\({P_3}):y = 4{x^2} - 8x + 7;\\({P_4}):y = - 3{x^2} - 6x - 1.\end{array}\)

Vì 4 đồ thị hàm số cắt trục tung tại 4 điểm phân biệt nên ta chỉ cần xác định tọa độ giao điểm của mỗi hàm số với trục tung là có thể phân biệt 4 đồ thị hàm số.
Đồ thị hàm số \(({P_1}):y = - 2{x^2} - 4x + 2\) cắt trục tung tại điểm có tung độ bằng 2, tức là đồ thị đi qua điểm có tọa độ (0; 2) => Đồ thị là đường màu xanh lá.
Đồ thị hàm số \(({P_2}):y = 3{x^2} - 6x + 5;\) cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5) => Đồ thị là đường màu xanh dương.
Đồ thị hàm số \(({P_3}):y = 4{x^2} - 8x + 7;\) cắt trục tung tại điểm có tung độ bằng 7, tức là đồ thị đi qua điểm có tọa độ (0; 7) => Đồ thị là đường màu nâu đỏ.
Đồ thị hàm số \(({P_4}):y = - 3{x^2} - 6x - 1\) cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1) => Đồ thị là đường màu vàng.
Tìm tập xác định của các hàm số sau:
a) 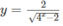
b) 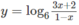
c) 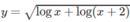
d) 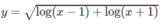
a) Hàm số xác định khi:
4 x – 2 > 0 ⇔ 2 2 x > 2 ⇔ x > 1/2
Vậy tập xác định là D = (1/2; + ∞ )
b) D = (−2/3; 1)
c) logx + log(x + 2) ≥ 0
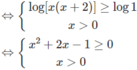
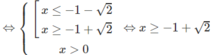
Vậy tập xác định là D = [−1 + 2 ; + ∞ )
d) Tương tự câu c, D = [ 2 ; + ∞ ).
Tìm tập xác định của các hàm số sau:
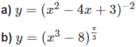
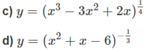
a) Hàm số xác định khi x 2 − 4x + 3 ≠ 0 hay x ≠ 1; x ≠ 3.
Vậy tập xác định của hàm số đã cho là R \ {1;3}.
b) Hàm số xác định khi x 3 – 8 > 0 hay x > 2. Vậy tập xác định là (2; + ∞ ).
c) Hàm số xác định khi x 3 – 3 x 2 + 2x > 0 hay x(x – 1)(x – 2) > 0
Tìm tập xác định của các hàm số sau:
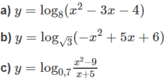
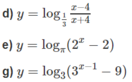
Tìm tập xác định và tập giá trị của các hàm số sau: