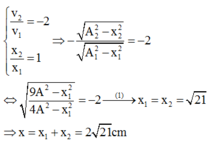Quan sát Hình 1.7, so sánh biên độ và li độ của hai dao động 1 và 2 tại mỗi thời điểm.
Những câu hỏi liên quan
SGK Chân trời sáng tạo - Trang 10
15 tháng 7 2023 lúc 11:40
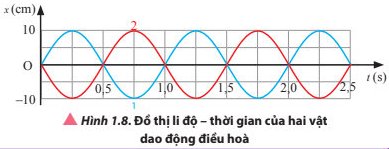
Quan sát đồ thị li độ - thời gian của hai dao động điều hòa được thể hiện trong Hình 1.8. Hãy xác định biên độ, chu kì, tần số, tần số góc của mỗi vật dao động và độ lệch pha giữa hai dao động.
Hai dao động có cùng biên độ.
Ở cùng một thời điểm khi dao động 1 ở vị trí cân bằng thì dao động 2 ở vị trí bên và ngược lại.
Đúng 0
Bình luận (0)
SGK Cánh diều - Trang 32
15 tháng 7 2023 lúc 23:48
Cho hai vật dao động điều hoà (1) và (2) có đồ thị li độ – thời gian như Hình 1.a) Xác định biên độ, chu kì và tần số của hai dao động.b) Xác định độ lệch pha của hai dao động ra đơn vị độ và rad.c) Tìm vận tốc của vật (2) tại thời điểm 3,5 s.d) Tìm gia tốc của vật (1) tại thời điểm 1,5 s.
Đọc tiếp
Cho hai vật dao động điều hoà (1) và (2) có đồ thị li độ – thời gian như Hình 1.
a) Xác định biên độ, chu kì và tần số của hai dao động.
b) Xác định độ lệch pha của hai dao động ra đơn vị độ và rad.
c) Tìm vận tốc của vật (2) tại thời điểm 3,5 s.
d) Tìm gia tốc của vật (1) tại thời điểm 1,5 s.
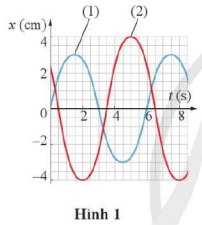
a) Dao động 1 (đường màu xanh) có:
- Biên độ: A1 = 3 cm
- Chu kì: T = 6 s
- Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{6}\left(Hz\right)\)
Dao động 2 (đường màu đỏ) có:
- Biên độ: A2 = 4 cm
- Chu kì: T = 6 s
- Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{6}\left(Hz\right)\)
b) Hai dao động có cùng chu kì nên \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{6}=\dfrac{\pi}{3}\left(rad/s\right)\)
Độ lệch thời gian của hai dao động khi cùng trạng thái: \(\Delta t=2,5s\)
Độ lệch pha: \(\Delta\varphi=\omega.\Delta t=\dfrac{\pi}{3}\cdot2,5=150^o\)
Đúng 0
Bình luận (0)
c) Tại thời điểm 3,5 s vật 2 đang ở VTCB nên vận tốc cực đại:
\(v=\omega A_2=\text{ }\dfrac{\pi}{3}\cdot4=\dfrac{4\pi}{3}\left(cm/s\right)\)
d) Tại thời điểm 1,5 s vật 1 đang ở biên dương nên gia tốc có giá trị:
\(a=-\omega^2A_1=-\dfrac{\pi^2}{9}\cdot3=-\dfrac{\pi^2}{3}\left(cm/s^2\right)\)
Độ lớn gia tốc khi đó là \(\dfrac{\pi^2}{3}cm/s^2\)
Đúng 0
Bình luận (0)
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số. Biết dao động thứ nhất có biên độ
A
1
6 cm và trễ pha p/2 so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ 9 cm. Biên độ dao động tổng hợp bằng A. 12 cm B. 18 cm C.
6
3
cm D.
9...
Đọc tiếp
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số. Biết dao động thứ nhất có biên độ A 1 = 6 cm và trễ pha p/2 so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ 9 cm. Biên độ dao động tổng hợp bằng
A. 12 cm
B. 18 cm
C. 6 3 cm
D. 9 3 cm
Đáp án C
* Li độ tổng hợp bằng tổng li độ hai dao động thành phần:
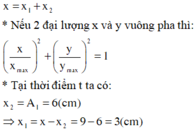
* Do dao động thứ nhất và dao động thành phần vuông pha nên:
Đúng 0
Bình luận (0)
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số. Biết dao động thứ nhất có biên độ A1 6 cm và trễ pha
π
/
2
so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ 9 cm. Biên độ dao động tổng hợp bằng A.
12
c
m
B.
6
3
c...
Đọc tiếp
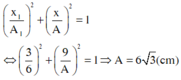
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số. Biết dao động thứ nhất có biên độ A1 = 6 cm và trễ pha π / 2 so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ 9 cm. Biên độ dao động tổng hợp bằng
A. 12 c m
B. 6 3 c m
C. 18 c m
D. 9 3 c m
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số. Biết dao động thứ nhất có biên độ
A
1
6 cm và trễ pha π/2 so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ 9 cm. Biên độ dao động tổng hợp bằng A. 6
3
cm. B. 9
3
cm. C...
Đọc tiếp
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số. Biết dao động thứ nhất có biên độ A 1 = 6 cm và trễ pha π/2 so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ 9 cm. Biên độ dao động tổng hợp bằng
A. 6 3 cm.
B. 9 3 cm.
C. 12cm.
D. 18cm.
+ Li độ tổng hợp bằng tổng li độ hai dao động thành phần: 
+ Nếu 2 đại lượng x và y vuông pha thì:
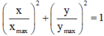
+ Tại thời điểm t ta có: 
+ Do dao động thứ nhất và dao động thứ hai vuông pha nên:
Đúng 0
Bình luận (0)
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số. Biết dao động thứ nhất có biên độ A1 6 cm và trễ pha
π
/
2
so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ 9 cm. Biên độ dao động tổng hợp bằng A. 12cm B. 18cm C.
6
3
c
m
D.
9...
Đọc tiếp
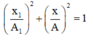
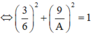
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số. Biết dao động thứ nhất có biên độ A1 = 6 cm và trễ pha π / 2 so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ 9 cm. Biên độ dao động tổng hợp bằng
A. 12cm
B. 18cm
C. 6 3 c m
D. 9 3 c m
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương cùng tần số. Biết dao động thứ nhất có biên độ A1 6 cm và trễ pha
π
/
2
so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ 9 cm. Biên độ dao động tổng hợp bằng A. 18 cm B. 12 cm C.
9
3
cm D.
6
3
Đọc tiếp
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương cùng tần số. Biết dao động thứ nhất có biên độ A1 = 6 cm và trễ pha π / 2 so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ 9 cm. Biên độ dao động tổng hợp bằng
A. 18 cm
B. 12 cm
C. 9 3 cm
D. 6 3
Đáp án D
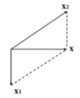
Phương pháp: Sử dụng̣ giản đồ Fresnen
Cách giải:
x1 + x2 = x => x1 +6 = 9cm => x1 = 3cm
Dựa vào đề bài ta biểu diễn được các vecto dao động như hình bên:
Đúng 0
Bình luận (0)
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số. Biết dao động thứ nhất có biên độ
A
1
6 cm và trễ pha 0,5π so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ bằng 9 cm. Biên độ của dao động tổng hợp bằng A. 18 cm B. 12 cm C.
9
3
cm
D.
6
3...
Đọc tiếp
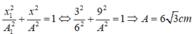
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số. Biết dao động thứ nhất có biên độ A 1 = 6 cm và trễ pha 0,5π so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ bằng 9 cm. Biên độ của dao động tổng hợp bằng
A. 18 cm
B. 12 cm
C. 9 3 cm
D. 6 3 cm
Dao động của một chất điểm là sự tổng hợp của hai dao động điều hòa với phương trình lần lượt là và . Tại thời điểm mà tỉ số vận tốc và tỉ số li độ của dao động thứ hai so với dao động thứ nhất lần lượt là 1 và -2 thì li độ dao động tổng hợp bằng
15
cm. Tại thời điểm mà tỉ số vận tốc và tỉ số li độ của dao động thứ hai so với dao động thứ nhất lần lượt là -2 và 1 thì li độ dao động tổng hợp của chất điểm có thể bằng A.
21
c...
Đọc tiếp
Dao động của một chất điểm là sự tổng hợp của hai dao động điều hòa với phương trình lần lượt là 
và 
. Tại thời điểm mà tỉ số vận tốc và tỉ số li độ của dao động thứ hai so với dao động thứ nhất lần lượt là 1 và -2 thì li độ dao động tổng hợp bằng
15
cm. Tại thời điểm mà tỉ số vận tốc và tỉ số li độ của dao động thứ hai so với dao động thứ nhất lần lượt là -2 và 1 thì li độ dao động tổng hợp của chất điểm có thể bằng
A. 21 cm
B. 2 15 cm
C. 15 cm
D. 2 21 cm
Giải thích: Đáp án D
Phương pháp: Sử dụng hê ̣thức độc lập theo thời gian của x và v
Cách giải:
- Tại thời điểm t:
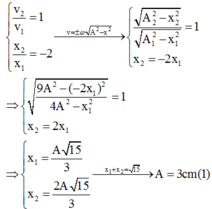
- Tại thời điểm t + ∆t: 
Đúng 0
Bình luận (0)