Vận dụng được công thức \(E=\dfrac{\left|Q\right|}{4\pi\varepsilon_0r^2}\) để tính toán và mô tả điện trường của hệ nhiều điện tích, vật tích điện hình cầu.

Những câu hỏi liên quan
Xét điện trường của điện tích Q = 6.10-14 C, sử dụng đoạn thẳng dài 1 cm để biểu diễn cho độ lớn vectơ cường độ điện trường \(E=\dfrac{10^{-10}}{6\pi\varepsilon_0}\) (V/m). Hãy tính và vẽ vectơ cường độ điện trường tại một điểm cách Q một khoảng 2 cm và 3 cm.
Đoạn thẳng 1cm biểu diễn cho độ lớn của cường độ điện trường \(E = \frac{{{{10}^{ - 10}}}}{{6\pi {\varepsilon _0}}} = 0,6\)V/m.
Cường độ điện trường tại điểm cách Q một khoảng 2 cm:
\(E = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}} = \frac{{\left| {{{6.10}^{ - 14}}} \right|}}{{4\pi 8,{{85.10}^{ - 12}}.0,{{02}^2}}} = 1,34\)V/m
Vectơ cường độ điện trường:
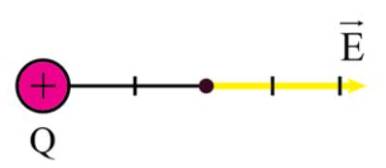
Cường độ điện trường tại điểm cách Q một khoảng 3 cm:
\(E = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}} = \frac{{\left| {{{6.10}^{ - 14}}} \right|}}{{4\pi 8,{{85.10}^{ - 12}}.0,{{03}^2}}} = 0,6\)V/m
Vectơ cường độ điện trường:
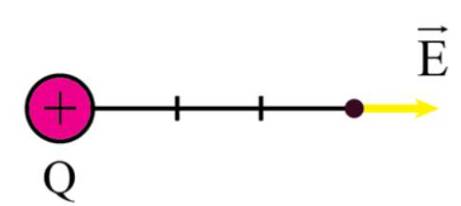
Đúng 0
Bình luận (0)
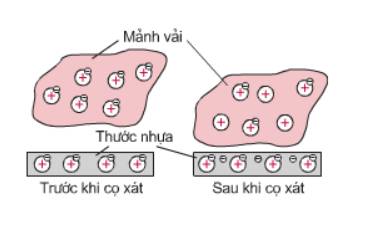
Sử dụng dấu cộng (+) để mô tả điện tích dương và dấu trừ (-) để mô tả điện tích âm, em hãy vẽ vào vở hai vật có hình dạng bất kì để mô tả:
Sau khi cọ xát, một vật trở nên nhiễm điện dương, vật kia trở nên nhiễm điện âm.
Để đặt một điện tích q vào điểm M trong điện trường chúng ta cần cung cấp thế năng WM cho điện tích q. Điều này tương ứng với việc thực hiện một công A dịch chuyển điện tích q từ vô cực về điểm M. Hãy vận dụng công thức (19.3) và (19.4) để thu được công thức: Vdfrac{A}{q}W_MA_{Minfty} (19.3)W_MV_Mq (19.4)
Đọc tiếp
Để đặt một điện tích q vào điểm M trong điện trường chúng ta cần cung cấp thế năng WM cho điện tích q. Điều này tương ứng với việc thực hiện một công A dịch chuyển điện tích q từ vô cực về điểm M. Hãy vận dụng công thức (19.3) và (19.4) để thu được công thức: \(V=\dfrac{A}{q}\)
\(W_M=A_{M\infty}\) (19.3)
\(W_M=V_Mq\) (19.4)
Công thức 19.2:
\(W_M=A_{M\infty}\)
Công thức 19.3:
\(W_M=V_Mq\)
Điện thế tại điểm M:
\(V_M=\dfrac{W_M}{q}=\dfrac{A_{M\infty}}{q}\) và \(V=\dfrac{A}{q}\)
Đúng 3
Bình luận (0)
Một quả cầu nhỏ có khối lượng 5 g và mang điện tích q=- 10‐⁶ C được thả nhẹ tại điểm M trong điện trường đều vector E có độ lớn E = 10³ V/m. Sau thời gian t= 2 s, vật chuyển động đến điểm N. Xem vật chỉ chịu tác dụng của lực điện, hãy tính hiệu điện thế giữa hai điểm M và N.
Lực điện tác dụng lên quả cầu là: \(F=E\left|q\right|=10^3.10^{-6}=10^{-3}N\)
mà F=ma \(\Rightarrow a=\dfrac{F}{m}=\dfrac{10^{-3}}{5.10^{-3}}=0,2\)m/s2
Có: \(MN=\dfrac{1}{2}at^2=\dfrac{1}{2}.0,2.2^2=0,4m\)
Hiệu điện thế giữa hai điểm MN là: \(V_{MN}=E.MD=10^3.0,4=400V\)
Đúng 1
Bình luận (0)
Gọi E là suất điện động của nguồn điện, A là công của nguồn điện, q là độ lớn điện tích dương. Mối liên hệ giữa ba đại lượng trên được diễn tả bởi công thức nào sau đây? A. E. q A B. q A.E C. E q.A D. A q2. E
Đọc tiếp
Gọi E là suất điện động của nguồn điện, A là công của nguồn điện, q là độ lớn điện tích dương. Mối liên hệ giữa ba đại lượng trên được diễn tả bởi công thức nào sau đây?
A. E. q = A
B. q = A.E
C. E = q.A
D. A = q2. E
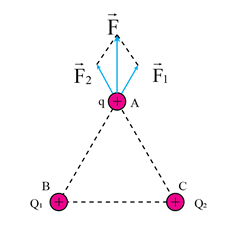
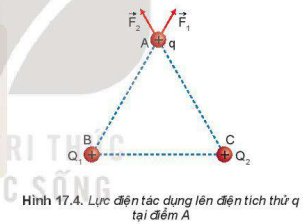
Nếu trong không gian có hai điện tích điểm dương Q1 = Q2 được đặt ở hai điểm B và C, một điện tích thử q được đặt tại một điểm A như Hình 17.4. Hãy mô tả bằng hình vẽ lực điện tổng hợp do Q1 và Q2 tác dụng lên điện tích thử q.
I. Điện tích q 5.10-9C di chuyển trong điện trường đều. Tác dụng của lực điện F 0,02N. Tính cường độ điện trường E.
II. Cho điện tích Q 2nC.
1. Tính cường độ điện trường tại điểm M cách Q 20cm.
2. Vẽ hình.
III. Điện tích q 2μC di chuyển trong điện trường đều. Tác dụng của lực điện F 2.10-3N. Tính cường độ điện trường E.
IV. Cho điện tích Q -2nC.
1. Tính cường độ điện trường tại điểm M cách Q 10cm.
2. Vẽ hình.
Giải giúp mình nhé. Help!!!
Đọc tiếp
I. Điện tích q = 5.10-9C di chuyển trong điện trường đều. Tác dụng của lực điện F = 0,02N. Tính cường độ điện trường E.
II. Cho điện tích Q = 2nC.
1. Tính cường độ điện trường tại điểm M cách Q 20cm.
2. Vẽ hình.
III. Điện tích q = 2μC di chuyển trong điện trường đều. Tác dụng của lực điện F = 2.10-3N. Tính cường độ điện trường E.
IV. Cho điện tích Q = -2nC.
1. Tính cường độ điện trường tại điểm M cách Q 10cm.
2. Vẽ hình.
Giải giúp mình nhé. Help!!!
Trong mạch điện gồm R,L,C mắc nối tiếp.\(R=30\Omega\) ,\(L=\dfrac{0,5}{\pi}mH\),\(C=\dfrac{50}{\pi}MF\)
\(u=100\sqrt{2}cos\left(100\pi t+\dfrac{\pi}{6}\right)\)
a,Tính hệ số công suất b,Tính biểu thức i
Hãy chứng tỏ rằng: Độ lớn cường độ điện trường tại một điểm trong công thức (17.1) bằng độ lớn của lực điện tác dụng lên một đơn vị điện tích đặt tại điểm đó.
\(E=\dfrac{F}{q}\) (17.1)
Độ lớn cường độ điện trường tại 1 điểm:
\(E=k\dfrac{\left|Q\right|}{r^2}\)
Lực điện tác dụng lên một đơn vị điện tích đặt tại điểm đó:
\(E=\dfrac{F}{q}=\dfrac{k\dfrac{\left|Q\cdot q\right|}{r^2}}{q}=k\dfrac{\left|Q\right|}{r^2}\)
Chứng tỏ: Độ lớn cường độ điện trường tại một điểm bằng độ lớn của lực điện tác dụng lên một đơn vị điện tích đặt tại điểm đó.
Đúng 1
Bình luận (0)