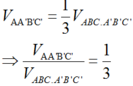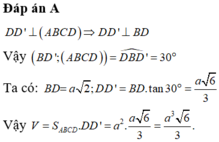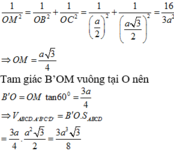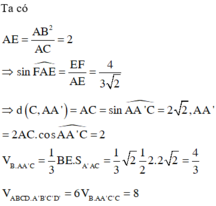Vẽ hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình bình hành

Những câu hỏi liên quan
Cho hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình bình hành. Tỉ số thể tích của khối tứ diện AA B C và khối lăng trụ đã cho là: A.
1
2
B.
3
4
C.
1
3
D.
1
6...
Đọc tiếp
Cho hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình bình hành. Tỉ số thể tích của khối tứ diện AA 'B 'C và khối lăng trụ đã cho là:
A. 1 2
B. 3 4
C. 1 3
D. 1 6
Lăng trụ đứng ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh a và đường chéo BD’ của lăng trụ hợp với đáy ABCD một góc 30º. Thể tích của lăng trụ là: A.
a
3
6
3
B.
a
3
6
8
C.
a...
Đọc tiếp
Lăng trụ đứng ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh a và đường chéo BD’ của lăng trụ hợp với đáy ABCD một góc 30º. Thể tích của lăng trụ là:
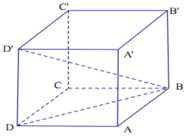
A. a 3 6 3
B. a 3 6 8
C. a 3 3
D. 3 a 3 6
Cho hình lăng trụ \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình bình hành. Chứng minh rằng:
a) Bốn mặt bên và mặt đáy còn lại của hình lăng trụ là các hình bình hành;
b) Các mặt \(AA'C'C\) và \(BB'D'D\)là hình bình hành
c) Bốn đoạn thẳng \(A'C,AC',B'D,BD\) có cùng trung điểm.
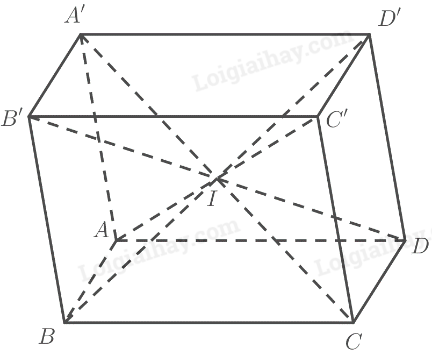
a) Vì \(ABCD.A'B'C'D'\) là hình lăng trụ nên có:
‒ Hai đáy \(ABCD\) và \(A'B'C'D'\) bằng nhau và là hình bình hành.
‒ Các mặt bên \(AA'B'B,AA'D'D,BB'C'C,CC'D'D\) là các hình bình hành.
b) Ta có:
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {AA'C'C} \right) \cap \left( {ABC{\rm{D}}} \right) = AC\\\left( {AA'C'C} \right) \cap \left( {A'B'C'D'} \right) = A'C'\end{array} \right\} \Rightarrow AC\parallel A'C'\)
Mà \(AA'\) và \(CC'\) là các cạnh bên của hình lăng trụ nên \(AA'\parallel CC'\)
Vậy \(AA'C'C\) là hình bình hành.
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {BB'D'D} \right) \cap \left( {ABC{\rm{D}}} \right) = B{\rm{D}}\\\left( {BB'D'D} \right) \cap \left( {A'B'C'D'} \right) = B'D'\end{array} \right\} \Rightarrow B{\rm{D}}\parallel B'D'\)
Mà \(BB'\) và \(DD'\) là các cạnh bên của hình lăng trụ nên \(BB'\parallel DD'\)
Vậy \(BB'D'D\) là hình bình hành.
c) Ta có:
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {A'B'C{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right) = C{\rm{D}}\\\left( {A'B'C{\rm{D}}} \right) \cap \left( {A'B'C'D'} \right) = A'B'\end{array} \right\} \Rightarrow C{\rm{D}}\parallel A'B'\left( 1 \right)\)
\(ABC{\rm{D}}\) là hình bình hành nên \(AB = CD\)
\(AA'B'B\) là hình bình hành nên \(AB = A'B'\)
Vậy \(A'B' = CD\left( 2 \right)\)
Từ (1) và (2) suy ra \(A'B'C{\rm{D}}\) là hình bình hành
\( \Rightarrow A'C,B'D\) cắt nhau tại trung điểm của mỗi đường.
Chứng minh tương tự ta có:
+ \(ABC'D'\) là hình bình hành nên \(AC',B{\rm{D}}'\) cắt nhau tại trung điểm của mỗi đường
+ \(A'BCD'\) là hình bình hành nên \(A'C,B{\rm{D}}'\) cắt nhau tại trung điểm của mỗi đường
Do đó bốn đoạn thẳng \(A'C,AC',B'D,BD\) có cùng trung điểm.
Đúng 0
Bình luận (0)
Cho hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a,
A
B
C
^
60
°
. Chân đường cao hạ từ B’ trùng với tâm O của đáy ABCD; góc giữa mặt phẳng (BBC’C) với đáy bằng 600. Thể tích lăng trụ bằng: A.
3
a
3
3
8
B. ...
Đọc tiếp
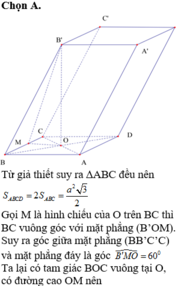
Cho hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, A B C ^ = 60 ° . Chân đường cao hạ từ B’ trùng với tâm O của đáy ABCD; góc giữa mặt phẳng (BB'C’C) với đáy bằng 600. Thể tích lăng trụ bằng:
A. 3 a 3 3 8
B. 2 a 3 3 9
C. 3 a 3 2 8
D. 3 a 3 4
Cho hình lăng trụ đứng ABCD.MNPQ có đáy ABCD là hình bình hành có AB 6cm, BC 4cm , AM 5cm. Tính diện tích xung quanh của hình lăng trụ? A.
100
c
m
2
B.
120
c
m
2
C.
150
c
m
2
D.
200
c
m
2
Đọc tiếp
Cho hình lăng trụ đứng ABCD.MNPQ có đáy ABCD là hình bình hành có AB = 6cm, BC = 4cm , AM = 5cm. Tính diện tích xung quanh của hình lăng trụ?
A. 100 c m 2
B. 120 c m 2
C. 150 c m 2
D. 200 c m 2
Chu vi đáy là:
P = 2(AB + BC) = 2.(6 + 4) = 20cm
Diện tích xung quanh của hình lăng trụ đã cho là:
S x q = P . h = 20 . 5 = 100 ( c m 2 )
Chọn đáp án A
Đúng 0
Bình luận (0)
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thang vuông ABCD vuông tại A, B (AB // BC) và BC 12cm, AD 16cm, CD 5cm, đường cao AA’ 6cm. Thể tích của hình lăng trụ là A. 200
c
m
3
B. 250
c
m
3
C. 252
c
m
3
D. 410
c
m
3
Đọc tiếp
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thang vuông ABCD vuông tại A, B (AB // BC) và BC = 12cm, AD = 16cm, CD = 5cm, đường cao AA’ = 6cm. Thể tích của hình lăng trụ là
A. 200 c m 3
B. 250 c m 3
C. 252 c m 3
D. 410 c m 3
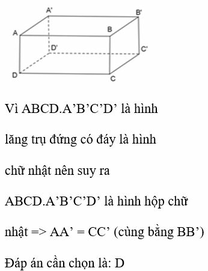
Cho hình lăng trụ đứng ABCD.A’B’C’D’, với mặt đáy ABCD là hình chữ nhật. Khi đó:
A. AA’ = CD’
B. BC’ = CD’
C. AC’ = BB’
D. AA’ = CC’
Cho lăng trụ ABCD.A’B’C’D’ với đáy ABCD là hình thoi,
A
C
2
a
,
B
A
D
^
120
∘
Hình chiếu vuông góc của điểm B trên mặt phẳng (A’B’C’D’) là trung điểm cạnh A’B’ góc giữa mặt phẳng (AC’D’) với mặt đáy là 60 độ. Tính thể tích V của lăng trụ ABCD.A’B’C’D’ A.
V
2
a...
Đọc tiếp
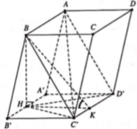
Cho lăng trụ ABCD.A’B’C’D’ với đáy ABCD là hình thoi, A C = 2 a , B A D ^ = 120 ∘ Hình chiếu vuông góc của điểm B trên mặt phẳng (A’B’C’D’) là trung điểm cạnh A’B’ góc giữa mặt phẳng (AC’D’) với mặt đáy là 60 độ. Tính thể tích V của lăng trụ ABCD.A’B’C’D’
A. V = 2 a 3 3
B. V = 3 a 3 3
C. V = a 3 3
D. V = 6 a 3 3
Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật với
A
B
6
,
A
D
3
,
A
C
3
và mặt phẳng
A
A
C
C
vuông góc với mặt đáy. Biết hai mặt phẳng tạo với nhau góc thỏa mãn...
Đọc tiếp
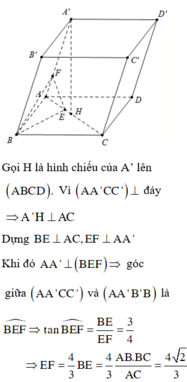
Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật với A B = 6 , A D = 3 , A ' C = 3 và mặt phẳng A A ' C ' C vuông góc với mặt đáy. Biết hai mặt phẳng tạo với nhau góc thỏa mãn tan α = 3 4 . Thể tích khối lăng trụ ABCD.A’B’C’D’ bằng
A. V = 8
B. V = 12
C. V = 10
D. V = 6