Cho biết phương trình: ax2+ bx+ c= 0 (a khác 0) có hai nghiệm x1; x2. Đặt Sn= x1n+ x2n (n thuộc N*). Chứng minh rằng: aSn+2+ bSn+1+ cSn =0.

Những câu hỏi liên quan
Cho phuong trình bậc hai ax2 + bx+ c =0 có hai nghiệm x1,x2 deu khác 0 . Phương trình bậc hai nhận 2x1 và 2x2 làm nghiệm là:
x1+x2=-b/a; x1x2=c/a
=>2x1+2x2=-2b/a; 4x1x2=4c/a
=>PT cần tìm là x^2+2b/a*x+4c/a=0
Đúng 0
Bình luận (0)
Chọn phát biểu đúng: Phương trình
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
có hai nghiệm
x
1
;
x
2
. Khi đó: A.
x
1
+...
Đọc tiếp
Chọn phát biểu đúng: Phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có hai nghiệm x 1 ; x 2 . Khi đó:
A. x 1 + x 2 = − b a x 1 . x 2 = c a
B. x 1 + x 2 = b a x 1 . x 2 = c a
C. x 1 + x 2 = − b a x 1 . x 2 = − c a
D. x 1 + x 2 = b a x 1 . x 2 = − c a
Cho phương trình bậc hai a x 2 + b x + c = 0 ( a ≠ 0 ) . Nếu x 1 ; x 2 là hai nghiệm của phương trình thì x 1 + x 2 = − b a x 1 . x 2 = c a
Đáp án: A
Đúng 0
Bình luận (0)
Cho phương trình ax2 + bx + c = 0 ( a ≠ 0 ) có hai nghiệm phân biệt x1, x2thoả x1 = x2^2 . Chứng minh b3 + a 2c + ac 2 = 3abc
theo bài ra ta có
n = 8a +7=31b +28
=> (n-7)/8 = a
b= (n-28)/31
a - 4b = (-n +679)/248 = (-n +183)/248 + 2
vì a ,4b nguyên nên a-4b nguyên => (-n +183)/248 nguyên
=> -n + 183 = 248d => n = 183 - 248d (vì n >0 => d<=0 và d nguyên )
=> n = 183 - 248d (với d là số nguyên <=0)
vì n có 3 chữ số lớn nhất => n<=999 => d>= -3 => d = -3
=> n = 927
Đúng 0
Bình luận (0)
sao 2 thằng giải trên giống trong yahoo hỏi đáp vậy
Đúng 0
Bình luận (0)
3. Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc hai
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
Nêu điều kiện để phương trình
a
x
2
+
b
x
+
c
0
(a ≠...
Đọc tiếp
3. Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc hai
a x 2 + b x + c = 0 ( a ≠ 0 )
Nêu điều kiện để phương trình a x 2 + b x + c = 0 (a ≠ 0) có một nghiệm bằng 1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
1954 x 2 + 21 x – 1975 = 0
Nêu điều kiện để phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có một nghiệm bằng -1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
2005 x 2 + 104 x – 1901 = 0
Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc haiax2 + bx + c 0 (a ≠ 0)Nêu điều kiện để phương trình ax2 + bx + c 0 (a ≠ 0) có một nghiệm bằng 1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình1954x2 + 21x – 1975 0Nêu điều kiện để phương trình ax2 + bx + c 0 (a ≠ 0) có một nghiệm bằng -1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình2005x2 + 104x – 1901 0
Đọc tiếp
Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc hai
ax2 + bx + c = 0 (a ≠ 0)
Nêu điều kiện để phương trình ax2 + bx + c = 0 (a ≠ 0) có một nghiệm bằng 1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
1954x2 + 21x – 1975 = 0
Nêu điều kiện để phương trình ax2 + bx + c = 0 (a ≠ 0) có một nghiệm bằng -1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
2005x2 + 104x – 1901 = 0
Chọn phát biểu đúng. Phương trình
a
x
2
+
b
x
+
c
(
a
≠
0
)
có hai nghiệm
x
1
;
x
2
. Khi đó: A.
x
1
+
x...
Đọc tiếp
Chọn phát biểu đúng. Phương trình a x 2 + b x + c ( a ≠ 0 ) có hai nghiệm x 1 ; x 2 . Khi đó:
A. x 1 + x 2 = - b a x 1 . x 2 = c a
B. x 1 + x 2 = b a x 1 . x 2 = c a
C. x 1 + x 2 = - b a x 1 . x 2 = - c a
D. x 1 + x 2 = b a x 1 . x 2 = - c a
Đáp án A
Cho phương trình bậc hai a x 2 + b x + c ( a ≠ 0 ) .
Nếu x 1 ; x 2 là hai nghiệm của phương trình thì:
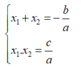
Đúng 0
Bình luận (0)
Cho phương trình bậc hai: ax2+bx+c=0 có hai nghiệm x1,x2thỏa mãn ax1+bx2+c=0. Tính M=a2c+ac2+b3-3abc+2018
Cho phương trình
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
có biệt thức
∆
b
2
–
4
a
c
0
. Khi đó, phương trình có hai nghiệm là: A.
x
1
x
2...
Đọc tiếp
Cho phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức ∆ = b 2 – 4 a c = 0 . Khi đó, phương trình có hai nghiệm là:
A. x 1 = x 2 = b 2 a
B. x 1 = − b 2 a ; x 2 = b 2 a
C. x 1 = − b + Δ 2 a ; x 2 = − b − Δ 2 a
D. x 1 = x 2 = - b 2 a
Xét phương trình bậc hai một ẩn
ax2 + bx + c = 0 (a ≠ 0) và biệt thức ∆ = b2 – 4ac
TH1: Nếu < 0 thì phương trình vô nghiệm
TH2. Nếu = 0 thì phương trình
có nghiệm kép x1 = x2 = − b 2 a
TH3: Nếu > 0 thì phương trình
có hai nghiệm phân biệt x1, 2 = − b ± Δ 2 a
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Cho phương trình
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
có biệt thức
∆
b
2
–
4
a
c
0
, khi đó, phương trình có hai nghiệm là: A.
x
1
...
Đọc tiếp
Cho phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức ∆ = b 2 – 4 a c > 0 , khi đó, phương trình có hai nghiệm là:
A. x 1 = x 2 = − b 2 a
B. x 1 = b + Δ 2 a ; x 2 = b − Δ 2 a
C. x 1 = − b + Δ 2 a ; x 2 = − b − Δ 2 a
D. x 1 = − b + Δ a ; x 2 = − b − Δ a
Xét phương trình bậc hai một ẩn
ax2 + bx + c = 0 (a ≠ 0) và biệt thức = b2 – 4ac
TH1: Nếu < 0 thì phương trình vô nghiệm
TH2. Nếu = 0 thì phương trình
có nghiệm kép x1 = x2 = − b 2 a
TH3: Nếu > 0 thì phương trình
có hai nghiệm phân biệt x1, 2 = − b ± Δ 2 a
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Cho phương trình
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
có biệt thức
Δ
b
2
-
4
a
c
. Khi đó phương trình có hai nghiệm là: A.
x
1
x
2
-...
Đọc tiếp
Cho phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức Δ = b 2 - 4 a c . Khi đó phương trình có hai nghiệm là:
A. x 1 = x 2 = - b 2 a
B. x 1 = b + △ 2 a ; x 2 = b - △ 2 a
C. x 1 = - b + △ 2 a ; x 2 = - b - △ 2 a
D. x 1 = - b + △ a ; x 2 = - b - △ a
Đáp án C
Xét phương trình bậc hai một ẩn và biệt thức
• TH1: Nếu thì phương trình vô nghiệm
• TH2: Nếu thì phương trình có nghiệm kép
x
1
=
x
2
= 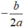
• TH3: Nếu thì phương trình có hai nghiệm phân biệt
x
1
,
2
= 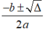
Đúng 0
Bình luận (0)












