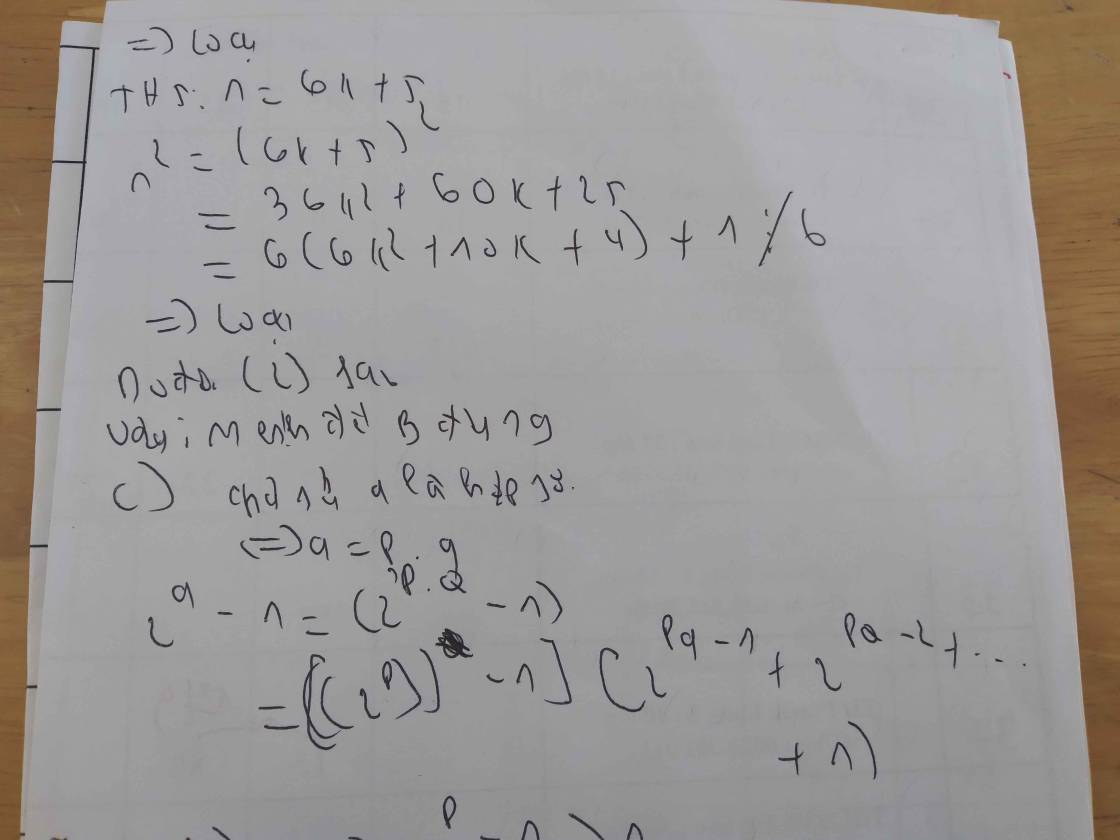CMR: nếu số nguyên n>1 thỏa mãn n2 + 4 và n2 + 16 là số nguyên tố thì n chia hết cho 5.

Những câu hỏi liên quan
Chứng minh rằng nếu số nguyên n lớn hơn 1 thoả mãn n2 + 4 và n2 +16 là các số nguyên tố thì n chia hết cho 5.
Ta có với mọi số nguyên m thì m2 chia cho 5 dư 0 , 1 hoặc 4.
+ Nếu n2 chia cho 5 dư 1 thì n 2 = 5 k + 1 = > n 2 + 4 = 5 k + 5 ⋮ 5 ; k ∈ N * .
Nên n2+4 không là số nguyên tố
+ Nếu n2 chia cho 5 dư 4 thì n 2 = 5 k + 4 = > n 2 + 16 = 5 k + 20 ⋮ 5 ; k ∈ N * .
Nên n2+16 không là số nguyên tố.
Vậy n2 ⋮ 5 hay n ⋮ 5
Đúng 0
Bình luận (0)
chứng minh rằng nếu số nguyên n lớn hơn 1 thỏa mãn n^2+4 và n^2+16 là các số nguyên tố thì n chia hết cho 5
CMR:
a) Nếu b là số nguyên tố khác 3 thì A=3n+2+2014b2 là hợp số với mọi số tự nhiên n
b) Nếu p và 8p2+1 là các số nguyên tố thì 8p2+2p+1 là số nguyên tố
c) Nếu k là số tự nhiên lớn hơn 1 thỏa mãn k2+4 và k2+16 là các số nguyên tố thì k chia hết cho 5
chứng minh rằng nếu n>1 thỏa mãn n2+4 và n2+16 là các số nguyên tố thì n chia hết cho 5
Đây toán 6 nha bạn
với n =2 => \(n^2+4=8 loại\)
với n =3 => \(n^2+16= 24 loại\)
với n =4 => \(n^2+4=20 loại\)
vói n =5 => ( các bn tự thử) THõa mãn
Với n>5 => n có dạng 5k+1,5k+2,5k+3,5K+4
Sau đó tự thử nha
Đúng 0
Bình luận (0)
Ta có tính chất số chính phương khi chia cho 5 có số dư là 0;1;4
Nếu n2 chia 5 dư 1 thì n2 = 5k + 1 => n2 + 4 = 5k + 5 chia hết cho 5
=> n2 + 4 không là SNT
Nếu n2 chia 5 dư 4 thì n2 = 5k + 4 => n2 + 16 = 5k + 20 chia hết cho 5
=> n2 + 16 không là SNT
Vậy n2 chia hết cho 5
Vậy ta có đpcm
cmr với mọi n thuộc N; n>1 thỏa mãn \(n^2+4\) và \(n^2+16\) là các số nguyên tố thì n chia hết cho 5
+, Nếu n chia 5 dư +-1 thì :
n^2 chia 5 dư 1 => n^2+4 chia hết cho 5
Mà n^2+4 > 5 => n^2+4 là hợp số
+, Nếu n chia 5 dư +-3 thì :
n^2 chia 5 dư 4 => n^2+16 chia hết cho 5
Mà n^2+16 > 5 => n^2+16 lừ hợp số
=> để n^2+4 và n^2+16 đều là số nguyên tố thì n chia hết cho 5
Tk mk nha
Đúng 0
Bình luận (0)
Xét tính Đ/S và c/m mệnh đề sau
A: '' nếu ∀ n ∈ N và n2 ⋮ 5 thì n⋮ 5 "
B: " ∀ x ∈ N và n2 ⋮ 6 thì n⋮ 6 "
C : '' nếu 2a - 1 là số nguyên tố thì a là số nguyên tố "
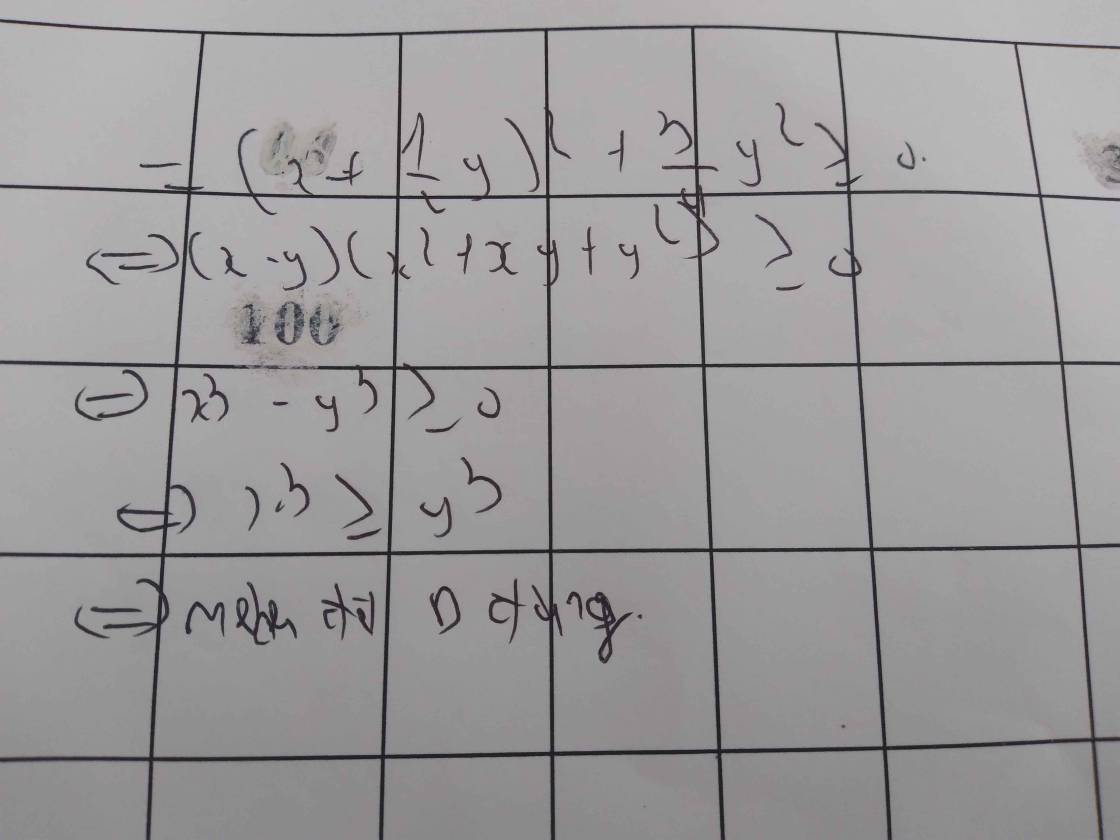
D: " nếu x≥y thì x3 ≥ y3 "
Chứng minh rằng nếu số nguyên n lớn hơn 1 và thỏa mãn \(n^2+4\)và \(n^2+16\) lấ các số nguyên tố thì n chia hết cho 5
1 nếu m, n là các số tự nhiên thỏa mãn 2m^2+m=3n^2+n thì m- n là số nguyên tố
2 chứng minh với n thuộc Z chẵn và n >4 thì n^4-4n^3-16n^2+16 chia hết cho 383
3 cho a, b là số chính phương lẻ. chứng minh (a-1((b-1) chia hết cho 192
4 tìm nghiệm nguyên tố của phương trình x^2- 2y= 1
chứng minh rằng số nguyên k lớn hơn 1 thỏa mãn k^2+4 và k^2+16 là số nguyên tố thì k chia hết cho 5
Ta có với mọi số nguyên m thì m2 chia cho 5 dư 0 , 1 hoặc 4. + Nếu n2 chia cho 5 dư 1 thì n 2 = 5 k + 1 = > n 2 + 4 = 5 k + 5 ⋮ 5 ; k ∈ N * . Nên n2+4 không là số nguyên tố + Nếu n2 chia cho 5 dư 4 thì n 2 = 5 k + 4 = > n 2 + 16 = 5 k + 20 ⋮ 5 ; k ∈ N * . Nên n2+16 không là số nguyên tố. Vậy n2 ⋮ 5 hay n ⋮ 5
Đúng 0
Bình luận (0)