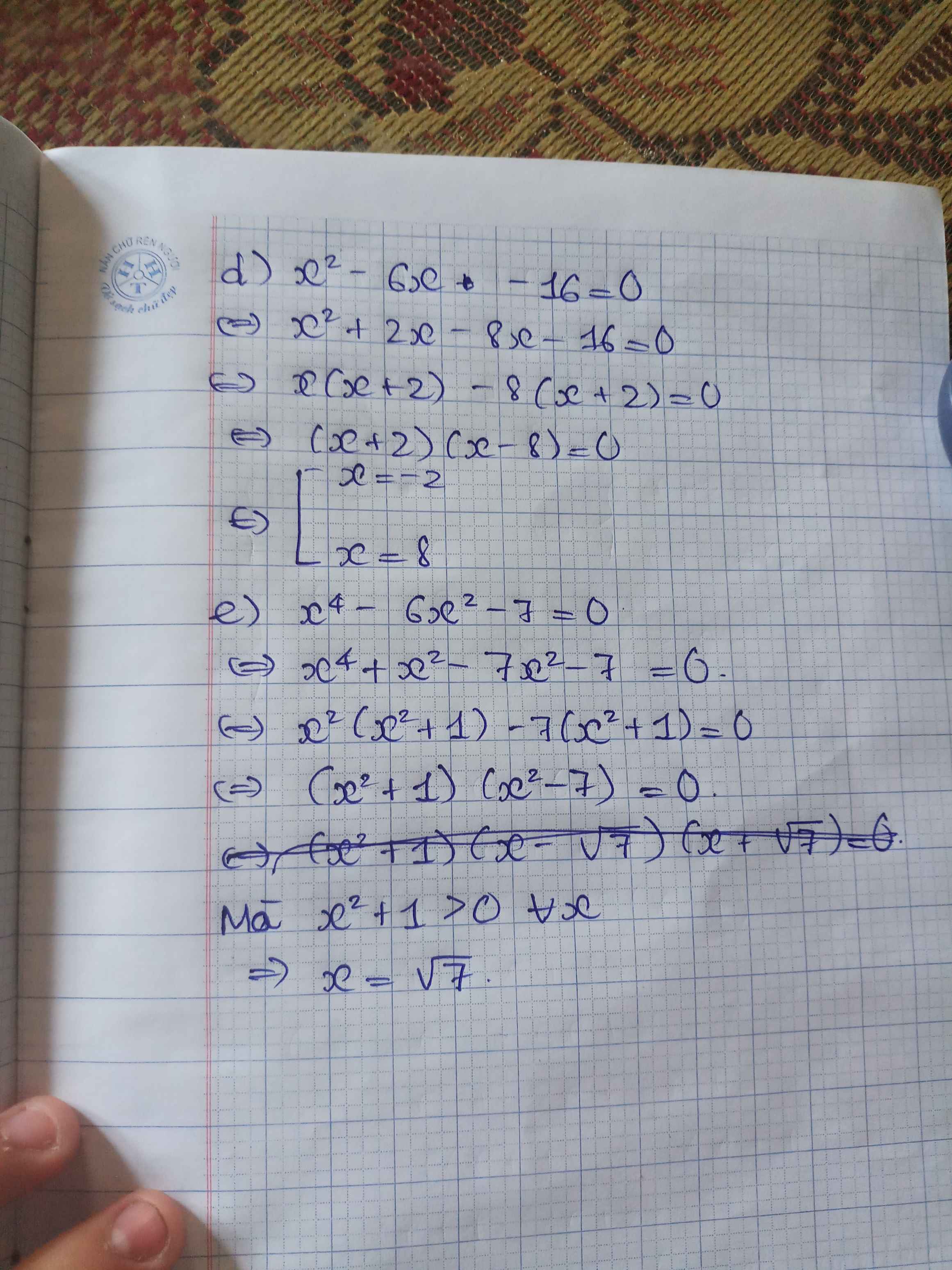a, \(\left(x-3\right)\left(x^2+x-20\right)\ge0\)

\(\Leftrightarrow\) \(\left(x-3\right)\left(x-4\right)\left(x+5\right)\ge0\)

+) \(x-3=0\Leftrightarrow x=3\); \(x-4=0\Leftrightarrow x=4\); \(x+5=0\Leftrightarrow x=-5\)

+) Lập trục xét dấu f(x) (Bạn tự kẻ trục nha)

\(\Rightarrow\) Bpt có tập nghiệm S = \(\left[-5;3\right]\cup\) [4; \(+\infty\))

b, \(\dfrac{x^2-4x-5}{2x+4}\ge0\)

\(\Leftrightarrow\) \(\dfrac{\left(x-5\right)\left(x+1\right)}{2x+4}\ge0\)

+) \(x-5=0\Leftrightarrow x=5\); \(x+1=0\Leftrightarrow x=-1\); \(2x+4=0\Leftrightarrow x=-2\)

+) Lập trục xét dấu f(x) 

\(\Rightarrow\) Bpt có tập nghiệm S = (-2; -1] \(\cup\) [5; \(+\infty\))

c, \(\dfrac{-1}{x^2-6x+8}\le1\)

\(\Leftrightarrow\) \(\dfrac{\left(x-3\right)^2}{\left(x-4\right)\left(x-2\right)}\ge0\)

+) \(x-3=0\Leftrightarrow x=3\); \(x-4=0\Leftrightarrow x=4\); \(x-2=0\Leftrightarrow x=2\)

+) Lập trục xét dấu f(x)

\(\Rightarrow\) Bpt có tập nghiệm S = (\(-\infty\); 2) \(\cup\) (4; \(+\infty\))

Chúc bn học tốt!

\(a.x^2-4x+4=0\)

\(\left(x-2\right)^2=0\)

=>x=2

b) \(2x^2-x=0\)

\(x\left(2x-1\right)=0\)

=> \(\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)

c) \(x^2-5x+6=0\)

\(x^2-2x-3x+6=0\)

\(\left(x-2\right)\left(x-3\right)=0\)

=> \(\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)

d) \(x^2+y^2=0\)

Vì \(x^2,y^2\ge0\forall x,y\)

=>x=y=0

e) \(x^2+6x+10=0\)

\(\left(x+3\right)^2+1=0\)

Vì \(\left(x+3\right)^2\ge0\forall x\)

=> VT>0 \(\forall x\)

=> phương trình vô nghiệm

a) \(x^2-4x+4=0\)

\(\Leftrightarrow\left(x-2\right)^2=0\)

\(\Leftrightarrow x-2=0\)

\(\Leftrightarrow x=2\)

b) \(2x^2-x=0\)

\(\Leftrightarrow x\left(2x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\2x-1=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)

c) \(x^2-5x+6=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\) \(\left(a+b+c=0\right)\)

d) \(x^2+y^2=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2=0\\y^2=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\)

e) \(x^2+6x+10=0\)

\(\Leftrightarrow x^2+6x+9+1=0\)

\(\Leftrightarrow\left(x+3\right)^2+1=0\left(1\right)\)

mà \(\left(x+3\right)^2+1\ge1>0,\forall x\in R\)

Nên phương trình (1) vô nghiệm

\(a,\Rightarrow\left(2x-5\right)^2+2\left(2x-5\right)\left(x+2\right)+\left(x+2\right)^2=0\\ \Rightarrow\left(2x-5+x+2\right)^2=0\\ \Rightarrow3x-3=0\\ \Rightarrow x=1\\ b,\Rightarrow9-\left(x^2-5x\right)^2=9\\ \Rightarrow x^2-5x=0\\ \Rightarrow x\left(x-5\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)

\(a)\left(x-2\right)\left(x^2+2x-3\right)\ge0.\)

Đặt \(f\left(x\right)=\left(x-2\right)\left(x^2+2x-3\right).\)

Ta có: \(x-2=0.\Leftrightarrow x=2.\\ x^2+2x-3=0.\Leftrightarrow\left[{}\begin{matrix}x=1.\\x=-3.\end{matrix}\right.\)

Bảng xét dấu:

x                   \(-\infty\)       -3       1       2     \(+\infty\)

\(x-2\)                    -      |    -   |   -   0   +

\(x^2+2x-3\)         +     0    -   0  +   |    +

\(f\left(x\right)\)                     -     0    +  0   -  0   +

Vậy \(f\left(x\right)\ge0.\Leftrightarrow x\in\left[-3;1\right]\cup[2;+\infty).\)

\(b)\dfrac{x^2-9}{-x+5}< 0.\)

Đặt \(g\left(x\right)=\dfrac{x^2-9}{-x+5}.\)

Ta có: \(x^2-9=0.\Leftrightarrow\left[{}\begin{matrix}x=3.\\x=-3.\end{matrix}\right.\)

\(-x+5=0.\Leftrightarrow x=5.\)

Bảng xét dấu:

x            \(-\infty\)      -3       3        5       \(+\infty\)

\(x^2-9\)            +   0   -   0   +   |    +

\(-x+5\)          +    |   +   |    +  0    -

\(g\left(x\right)\)              +    0   -   0   +  ||    -

Vậy \(g\left(x\right)< 0.\Leftrightarrow x\in\left(-3;3\right)\cup\left(5;+\infty\right).\)

a) Ta có: \(36x^3-4x=0\)

\(\Leftrightarrow4x\left(9x^2-1\right)=0\)

\(\Leftrightarrow x\left(3x-1\right)\left(3x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{3}\\x=\dfrac{-1}{3}\end{matrix}\right.\)

b) Ta có: \(3x\left(x-2\right)+x-2=0\)

\(\Leftrightarrow\left(x-2\right)\left(3x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{-1}{3}\end{matrix}\right.\)

d) Ta có: \(x^2-6x-16=0\)

\(\Leftrightarrow\left(x-8\right)\left(x+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)

e) Ta có: \(x^4-6x^2-7=0\)

\(\Leftrightarrow\left(x^2-7\right)\left(x^2+1\right)=0\)

\(\Leftrightarrow x\in\left\{\sqrt{7};-\sqrt{7}\right\}\)

1. A

2. C 

Câu 1: A

Câu 2: C

Câu 2: 

a:

ĐKXĐ: \(x^2+3x>=0\)

=>x(x+3)>=0

=>\(\left[{}\begin{matrix}x>=0\\x< =-3\end{matrix}\right.\)

 \(\sqrt{16}-\sqrt{x^2+3x}=0\)

=>\(\sqrt{x^2+3x}=\sqrt{16}\)

=>x^2+3x=16

=>x^2+3x-16=0

\(\text{Δ}=3^2-4\cdot1\cdot\left(-16\right)=9+64=73>0\)

Do đó: Phương trình có 2 nghiệm phân biệt là:

\(\left\{{}\begin{matrix}x_1=\dfrac{-3-\sqrt{73}}{2}\\x_2=\dfrac{-3+\sqrt{73}}{2}\end{matrix}\right.\)

b:

ĐKXĐ: \(x\in R\)

 \(3x-1-\sqrt{4x^2-12x+9}=0\)

=>\(\sqrt{\left(2x-3\right)^2}=3x-1\)

=>\(\left\{{}\begin{matrix}3x-1>=0\\\left(3x-1\right)^2=\left(2x-3\right)^2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x>=\dfrac{1}{3}\\\left(3x-1-2x+3\right)\left(3x-1+2x-3\right)=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x>=\dfrac{1}{3}\\\left(x+2\right)\left(5x-4\right)=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\left(loại\right)\\x=\dfrac{4}{5}\left(nhận\right)\end{matrix}\right.\)

c:

ĐKXĐ: \(\left\{{}\begin{matrix}x^2-6x+8>=0\\2x^2-10x+11>=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x>=4\\x< =2\end{matrix}\right.\\\left[{}\begin{matrix}x< =\dfrac{5-\sqrt{3}}{2}\\x>=\dfrac{5+\sqrt{3}}{2}\end{matrix}\right.\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x< =\dfrac{5-\sqrt{3}}{2}\\x>=4\end{matrix}\right.\)

 \(\sqrt{2x^2-10x+11}=\sqrt{x^2-6x+8}\)

\(\Leftrightarrow2x^2-10x+11=x^2-6x+8\)

=>\(x^2-4x+3=0\)

=>(x-1)(x-3)=0

=>x=3(loại) hoặc x=1(nhận)

a. 

$x^4-6x^2+9=0$

$\Leftrightarrow (x^2-3)^2=0$

$\Leftrightarrow x^2-3=0$

$\Leftrightarrow x^2=3$

$\Leftrightarrow x=\pm \sqrt{3}$

b.

$8x^3+12x^2+6x-63=0$

$\Leftrightarrow (8x^2+12x^2+6x+1)-64=0$

$\Leftrightarrow (2x+1)^3=64=4^3$

$\Leftrightarrow 2x+1=4$

$\Leftrightarrow x=\frac{3}{2}$

c. $(3-2x)^2-25=0$

$\Leftrightarrow (3-2x)^2-5^2=0$

$\Leftrightarrow (3-2x-5)(3-2x+5)=0$

$\Leftrightarrow (-2-2x)(8-2x)=0$

$\Leftrightarrow -2-2x=0$ hoặc $8-2x=0$

$\Leftrightarrow x=-1$ hoặc $x=4$

d.

$6(x+1)^2-2(x+1)^3+2(x-1)(x^2+x+1)=1$

$\Leftrightarrow (x+1)^2[6-2(x+1)]+2(x^3-1)=1$

$\Leftrightarrow (x+1)^2(4-2x)+2x^3-3=0$

$\Leftrightarrow 6x+1=0$

$\Leftrightarrow x=\frac{-1}{6}$

e. $(x-2)^2-(x-2)(x+2)=0$

$\Leftrightarrow (x-2)[(x-2)-(x+2)]=0$

$\Leftrightarrow (x-2)(-4)=0$

$\Leftrightarrow x-2=0$

$\Leftrightarrow x=2$

f. $x^2-4x+4=25$

$\Leftrightarrow (x-2)^2=5^2=(-5)^2$

$\Leftrightarrow x-2=5$ hoặc $x-2=-5$

$\Leftrightarrow x=7$ hoặc $x=-3$

a. 

${}^{}-6{}^{}+9=0$

$\iff ({}^{}-3{}^{}=0$

$\iff {}^{}-3=0$

$\iff {}^{}=3$

$\iff x=\pm \sqrt{3}$

b.

$8{}^{}+12{}^{}+6x-63=0$

$\iff (8{}^{}+12{}^{}+6x+1)-64=0$

$\iff (2x+1{}^{}=64={}^{}$

$\iff 2x+1$