Rút gọn biểu thức sau
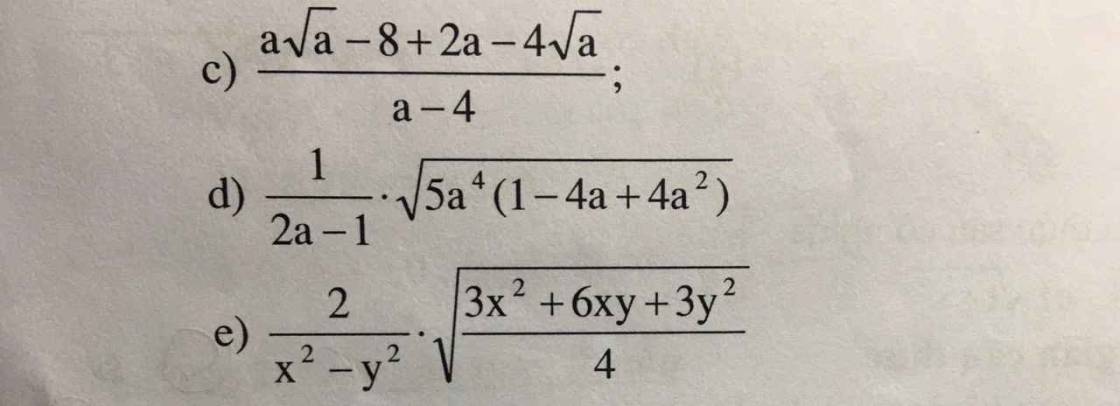
rút gọn biểu thức sau rồi tìm giá trị x dể biểu thức rút gọn duơng
(x^2-4x+4)/(x^3-2x^2-(4x-8))
rút gọn biểu thức sau rồi tìm giá trị x dể biểu thức rút gọn duơng
(x^2-4x+4)/(x^3-2x^2-(4x-8))
Rút gọn biểu thức sau, rồi tìm giá trị của x để giá trị của biểu thức rút gọn là 1 số dương:
\(\dfrac{8-2x}{x^2+x-20}\)
\(\dfrac{8-2x}{x^2+x-20}=-\dfrac{2\left(4-x\right)}{\left(4-x\right)\left(x+5\right)}=\dfrac{-2}{x+5}\)
Để biểu thức trên nhận giá trị dương khi
\(x+5< 0\)do -2 < 0
\(\Leftrightarrow x< -5\)
rút gọn các biểu thức sau rồi tính giá trị biểu thức
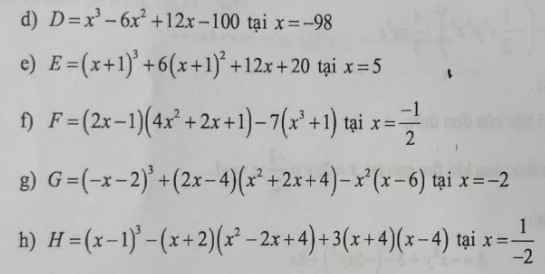
d: \(D=x^3-6x^2+12x-100\)
\(=x^3-6x^2+12x-8-92\)
\(=\left(x-2\right)^3-92\)
Khi x=-98 thì \(D=\left(-98-2\right)^3-92=-1000000-92=-1000092\)
e: \(E=\left(x+1\right)^3+6\left(x+1\right)^2+12x+20\)
\(=\left(x+1\right)^3+6\left(x+1\right)^2+12\left(x+1\right)+8\)
\(=\left(x+1+2\right)^3\)
\(=\left(x+3\right)^3\)
Khi x=5 thì \(E=\left(5+3\right)^3=8^3=512\)
f: \(F=\left(2x-1\right)\left(4x^2+2x+1\right)-7\left(x^3+1\right)\)
\(=\left(2x\right)^3-1^3-7x^3-7\)
\(=x^3-8\)
Khi x=-1/2 thì \(F=\left(-\dfrac{1}{2}\right)^3-8=-\dfrac{1}{8}-8=-\dfrac{65}{8}\)
g: \(G=\left(-x-2\right)^3+\left(2x-4\right)\left(x^2+2x+4\right)-x^2\left(x-6\right)\)
\(=-\left(x+2\right)^3+2\left(x-2\right)\left(x^2+2x+4\right)-x^3+6x^2\)
\(=-x^3-6x^2-12x-8+2\left(x^3-8\right)-x^3+6x^2\)
\(=-2x^3-12x-8+2x^3-16=-12x-24\)
Khi x=-2 thì \(G=-12\cdot\left(-2\right)-24=24-24=0\)
h: \(H=\left(x-1\right)^3-\left(x+2\right)\left(x^2-2x+4\right)+3\left(x+4\right)\left(x-4\right)\)
\(=x^3-3x^2+3x-1-\left(x^3+8\right)+3\left(x^2-16\right)\)
\(=x^3-3x^2+3x-1-x^3-8+3x^2-48\)
\(=3x-57\)
Khi x=-1/2 thì \(H=3\cdot\dfrac{-1}{2}-57=-1,5-57=-58,5\)
Rút gọn biểu thức sau ta được biểu thức nào sau đây?
A = c o s 2 x + sin 2 x + sin 2 x 2 sin x + c o s x
A. cosx
B. sinx
C. tanx
D. cotx
Đáp án: A
Ta có:
A = c o s 2 x + sin 2 x + sin 2 x 2 sin x + c o s x
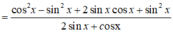
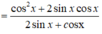
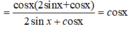
Rút gọn biểu thức sau
\(2\sqrt{3x}-\sqrt{75x}\)
\(=2\sqrt{3x}-5\sqrt{3x}\)
\(=-3\sqrt{3x}\)
Rút gọn biểu thức sau :
\(A=\sqrt[3]{\left(4-2\sqrt[3]{3}\right)\left(\sqrt[3]{3}-1\right)}\)
\(=\sqrt[3]{4\sqrt[3]{3}-4-2\sqrt[3]{9}+2\sqrt[3]{3}}\)
\(=\sqrt[3]{4-2\sqrt[3]{9}+6\sqrt[3]{3}}\)
Rút gọn biểu thức sau:
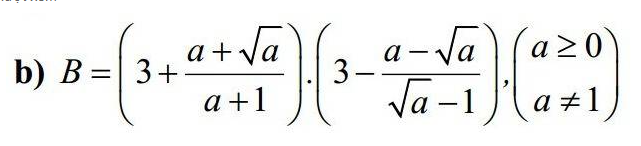
Rút gọn biểu thức sau:
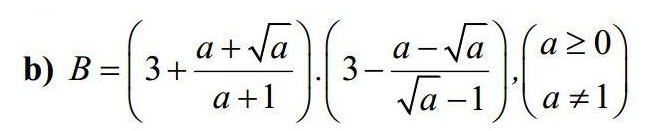
Rút gọn biểu thức sau:
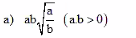
\(ab\sqrt{\dfrac{a}{b}}=a\cdot b\cdot\dfrac{\sqrt{a}}{\sqrt{b}}=a\sqrt{ab}\)