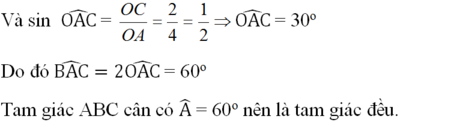Bài 26 (trang 115 SGK Toán 9 Tập 1)
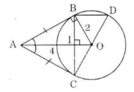
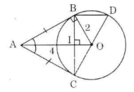
Cho đường tròn $(O)$, điểm $A$ nằm bên ngoài đường tròn. Kẻ các tiếp tuyến $AB$, $AC$ với đường tròn ($B$, $C$ là các tiếp điểm).
a) Chứng minh rằng $OA$ vuông góc với $BC$.
b) Vẽ đường kính $CD$. Chứng minh rằng $BD$ song song với $AO$.
c) Tính độ dài các cạnh của tam giác $ABC$; biết $OB = 2$cm, $OA = 4$cm.