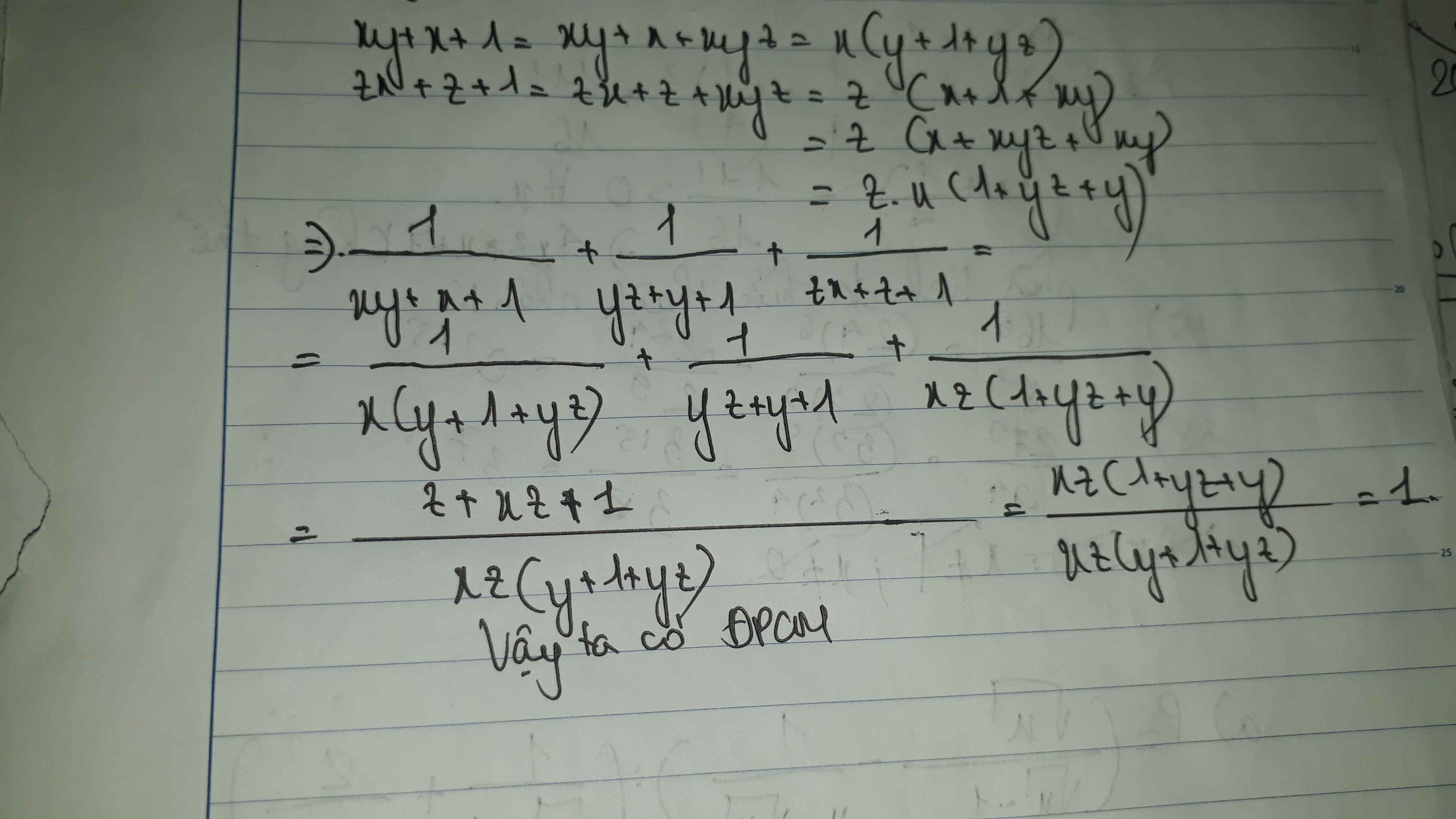ta có :

\(\frac{1}{xy+x+1}+\frac{y}{yz+y+1}+\frac{1}{xyz+yz+y}\)

\(\frac{xyz}{xy+x+xyz}+\frac{y}{yz+y+1}+\frac{xyz}{1+yz+y}\)

\(\frac{yz+y+xyz}{y+1+yz}\)

\(\frac{yz+y+1}{yz+y+1}\)

=1

luffy123 làm đúng mà sao vẫn có đứa bảo sai kìa

Ta có:

\(\frac{1}{xy+x+1}+\frac{y}{yz+y+1}+\frac{1}{xyz+yz+y}=\frac{xyz}{xy+x+xyz}+\frac{y}{yz+y+1}+\frac{1}{1+yz+y}\)

                                              \(=\frac{xyz}{x.\left(y+1+yz\right)}+\frac{y}{yz+y+1}+\frac{1}{1+yz+y}\)

                                              \(=\frac{yz}{y+1+yz}+\frac{y}{yz+y+1}+\frac{1}{1+yz+y}\)

                                               \(=\frac{yz+y+1}{yz+y+1}=1\left(đpcm\right)\)

\(\dfrac{1}{xy+x+1}+\dfrac{y}{yz+y+1}+\dfrac{1}{xyz+yz+y}\)

\(=\dfrac{xyz}{xy+x+xyz}+\dfrac{y}{yz+y+1}+\dfrac{1}{yz+y+1}\)

\(=\dfrac{xyz}{x\left(y+1+yz\right)}+\dfrac{y}{yz+y+1}+\dfrac{1}{yz+y+1}\)

\(=\dfrac{yz}{yz+y+1}+\dfrac{y}{yz+y+1}+\dfrac{1}{yz+y+1}\)

\(=\dfrac{yz+y+1}{yz+y+1}=1\left(đpcm\right)\)

Vậy...

Ta có \(\frac{x+2xy+1}{x+xy+xz+1}=\frac{x+2xy+xyz}{x+xy+xz+xyz}=\frac{1+2y+yz}{\left(y+1\right)\left(z+1\right)}\)

Tương tự => \(M=\frac{1+2y+yz}{\left(y+1\right)\left(z+1\right)}+\frac{1+2z+zx}{\left(1+x\right)\left(z+1\right)}+\frac{1+2x+xy}{\left(1+x\right)\left(y+1\right)}\)

=> \(M=\frac{\left(1+2y+yz\right)\left(1+x\right)+\left(1+2z+zx\right)\left(1+y\right)+\left(1+2x+xy\right)\left(1+z\right)}{\left(1+x\right)\left(1+y\right)\left(1+z\right)}\)

=>\(M=\frac{6+3\left(x+y+z\right)+3\left(xy+yz+xz\right)}{2+\left(x+y+z\right)+\left(xy+yz+xz\right)}=3\)

= 1 nhé

thay x.y.z zô biểu thức đi . rùi đặt nhân tử chung rùi tự làm , đến đó mà k làm dc nữa  thì die đi