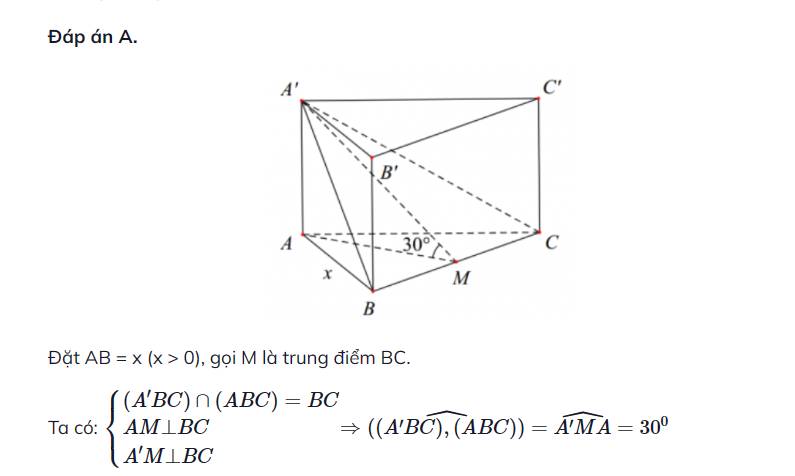
Mng ơi cho mình hỏi bài này tại sao A'M lại vuông với BC ạ, theo suy nghĩ của mình thì tại A' \(\in\)AA', AM vuông với BC nên A'M cũng vuông, mình nghĩ v có đúng k ạ :vv
Cho tam giácABC vuông tại A, có AB < AC.Trên cạnh huyền BC lấy điểm K sao cho CK=CA.Vẽ CM vuông góc AK tại M.Vẽ AD vuông góc BC tại D.AD cắt CM tại H.CM
a)TAM GIÁC MCK=TAM GIÁC MCA
b)HK//AB
c)HD<HA
MNG GIÚP MÌNH VỚI Ạ!!!
a/
Xét tg vuông MCA và tg vuông MCK có
CM chung
CA=CK (gt)
=> tg MCA = tg MCK (Hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau)
b/
Xét tg ACK có
\(CM\perp AK\) (gt)
\(AD\perp BC\) (gt)
=> H là trực tâm tg ACK => \(KH\perp AC\)
Mà \(AB\perp AC\)
=> KH//AB
c/
Xét tg vuông AMH và tg vuông KMH có
tg MCA = tg MCK (cmt) => MA=MK
MH chung
=> tg vuông AMH = tg vuông KMH (Hai tg vuông có hai cạnh góc vuông bằng nhau)
=> HA=HK (1)
Xét tg vuông KDH có
HD<HK (trong tg vuông cạnh huyền là cạnh có độ dài lớn nhất) (2)
Từ (1) và (2) => HD<HA
giúp tớ bài này đi mà làm ơn !!! mình sẽ tick cho :( cảm ơn ạ
Bài 5 (3,5 điểm)
Cho tam giác ABC vuông tại A< gọi M là trung điểm của BC. Kẻ MI vuông góc với AC tại I. Trên tia đối của tia IM lấy điểm N sao cho IN = IM. Gọi k là giao điểm AB và CN. Trên tia đối của MA lấy điểm E sao cho ME = MA. chứng minh:
a) ΔIMC = ΔINC
b) CB = CK và N là điểm trung CK
c) AB // CE
d) Ba điểm E, I, K thẳng hàng
mọi người chỉ cần làm ý b, c, d thui ạ,... mình cảm ơn :(
Tham khảo:
a) Xét ΔIMC vuông tại I và ΔINC vuông tại I có
CI chung
MI=NI(gt)
Do đó: ΔIMC=ΔINC(hai cạnh góc vuông)
b) Ta có: ΔIMC=ΔINC(cmt)
nên ˆMCI=ˆNCIMCI^=NCI^(hai góc tương ứng)
hay ˆBCA=ˆKCABCA^=KCA^
Xét ΔBAC vuông tại A và ΔKAC vuông tại A có
AC chung
ˆBCA=ˆKCABCA^=KCA^(cmt)
Do đó: ΔBAC=ΔKAC(cạnh góc vuông-góc nhọn kề)
⇒CB=CK(hai cạnh tương ứng)
Ta có: MI⊥AC(gt)
AB⊥AC(ΔABC vuông tại A)
Do đó: MI//AB(Định lí 1 từ vuông góc tới song song)
hay MN//KB
Xét ΔCKB có
M là trung điểm của CB(gt)
MN//KB(cmt)
Do đó: N là trung điểm của CK(Định lí 1 đường trung bình của tam giác)
c) Ta có: MA=ME(gt)
mà A,M,E thẳng hàng
nên M là trung điểm của AE
Xét tứ giác ABEC có
M là trung điểm của đường chéo BC(gt)
M là trung điểm của đường chéo AE(cmt)
Do đó: ABEC là hình bình hành(Dấu hiệu nhận biết hình bình hành)
hay AB//EC(Hai cạnh đối trong hình bình hành ABEC)
d) Ta có: ABEC là hình bình hành(cmt)
nên AB=EC(Hai cạnh đối trong hình bình hành ABEC)
mà AB=AK(ΔCBA=ΔCKA)
nên EC=AK
Ta có: AB//EC(Cmt)
nên CE//KA
Xét tứ giác AECK có
CE//AK(cmt)
CE=AK(cmt)
Do đó: AECK là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Xét ΔCAB có
M là trung điểm của BC(gt)
MI//AB(cmt)
Do đó: I là trung điểm của AC(Định lí 1 đường trung bình của tam giác)
Ta có: AECK là hình bình hành(cmt)
nên Hai đường chéo AC và EK cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà I là trung điểm của AC(cmt)
nên I là trung điểm của EK
hay E,I,K thẳng hàng(đpcm)
Mọi người ơi, giải dùm mình bài toán này với ạ. Cho mình cảm ơn trước.
Cho tam giác ABC vuông tại A có AC> AB. Gọi M là trung điểm của BC , đường trung trực của BC cắt AC tại E và cắt tia BA tại D. Chứng minh rằng :
a, A, M, C, D cùng thuộc một đường thẳng.
b, góc DBE bằng góc DMA
c, BC2= 2BA.BD
d, Gọi F là điểm đối xứng của E qua A. Hai đường thẳng MA và BF cắt nhau tại N. CM : góc BNC vuông
câu a, b,c thì mình giải được nhưng câu d giải k dc.
mình đang cần gấp, ai biết thì giải dùm với ạ.
Cô hướng dẫn em câu d nhé, theo cô thấy thì đề của em không đúng, góc vuông ở đây là BND nhé ^^
Do F đối xứng với E qua A nên tam giác BEF cân tại B, từ đó góc FBA = góc ABE. Lại do câu b, góc ABE = góc AMD nên góc NBD bằng góc NMD. Vậy tứ giác BMDN nội tiếp.
Ta thấy góc BMD vuông nên BD là đường kính. Từ đó góc DNB vuông (đpcm)
Chúc em học tốt :))))
cho tam giác ABC vuông tại A , K là trung điểm của cạnh BC . qua K kẻ đường thẳng vuông góc với AK , đường thẳng này cắt các đường thẳng AB và Ac lần lượt tại D và E. gọi I là trung điểm của De
a, Chứng minh :AI vuông góc với BC
b, Có thể nói DE nhỏ hơn BC được không?VÍ sao?
Mọi người ơi giúp mình với, mình đang cần làm bài này gấp .
Em tham khảo tại link dưới đây nhé:
Câu hỏi của Lê Xuân Huy - Toán lớp 7 - Học toán với OnlineMath
cho tam giác abc cân tại a . kẻ AK vuông góc bc tại k ( k thuộc bc )
a. cmr : kb = kc
b. kẻ km vuông góc ab ( m thuộc ab ) , kn vuông góc ac ( n thuộc ac )
so sánh : km và kn
c . cmr bc song song mn
[ kèm theo giả thiết và hình vẽ hộ mình nhé =))) nếu không thì giải hộ bài toán cũng được ^^ mình cần gấp lắm ạ . có gì mình sẽ hậu tạ sau ]
(Mình vẽ hình xấu hoắc à! Mà nhớ bài này giải rồi)
a) Ta có \(\Delta ABC\)cân tại \(A\Rightarrow AK\)vừa là đường cao vừa là trung tuyến (vừa là phân giác (*))
\(\Rightarrow KB=KC\)
b) Xét \(\Delta AMK\)và \(\Delta ANK\)có:
\(AK\): chung
\(\widehat{AMK}=\widehat{ANK}=90\)độ (gt)
\(\widehat{MAK}=\widehat{NAK}\)(Từ (*) ở câu a)
\(\Rightarrow\Delta AMK=\Delta ANK\left(g.c.g\right)\)
\(\Rightarrow KM=KN\)(hai cạnh tương ứng)
c) Từ cm câu b \(\Rightarrow AM=AN\)(hai cạnh tương ứng)
Ta có: \(\hept{\begin{cases}AM=AN\left(cmt\right)\\KM=KN\left(cmt\right)\end{cases}}\)
\(\Rightarrow AK\)là đường trung trực của \(MN\Rightarrow AK⊥MN\)
Ta lại có: \(\hept{\begin{cases}MN⊥AK\left(cmt\right)\\BC⊥AK\left(gt\right)\end{cases}}\)
\(\Rightarrow MN\)// \(BC\)
Trong tiềm thức của chúng ta, có lẽ ai cũng tự giễu với chính mình rằng:"tôi chỉ là con nuôi, con ghét của bố mẹ mà thôi..." đúng k? Và giờ lớn lên oy, bạn có còn ý nghĩ này nữa không ạ? Nếu đúng hoặc nếu sai thì các bạn hãy cho mik biết lí ro tại sao nhé
Mong mọi người hãy nói thật suy nghĩ của mình nhé, đừng ngại >_^
làm bừa thui,ai tích mình mình tích lại
Số số hạng là :
Có số cặp là :
50 : 2 = 25 ( cặp )
Mỗi cặp có giá trị là :
99 - 97 = 2
Tổng dãy trên là :
25 x 2 = 50
Đáp số : 50
Cho tam giác ABC vuông tại A, đường cao AH. a) vẽ HI vuông góc AB, vẽ HJ vuông góc AC. b) vẽ Bx vuông góc AB tại B và cắt tia AH tại E Giúp mình vẽ bài này với ạ, nghĩ hoài ko ra😓
Cho tam giác ABC vuông tại A, đường cao AH. a) vẽ HI vuông góc AB, vẽ HJ vuông góc AC. b) vẽ Bx vuông góc AB tại B và cắt tia AH tại E Giúp mình vẽ bài này với ạ, nghĩ hoài ko ra😓
ai giúp mình bài này vs ạ xd
Bài 3: Cho tam giác ABC vuông tại A có AB=18cm; AC=24cm. Gọi D là trung điểm BC. Đường vuông góc với BC tại D cắt AC tại M và cắt tia BA tại E. a) Chứng minh ∆𝐴𝐵𝐶 ~∆𝐷𝐵𝐸 , từ đó suy ra AB.DE = AC.DB b) Tính độ dài DE, BE c) Chứng minh MA.MC = MD.ME d) Chứng minh ∆𝑀𝐴𝐷 ~∆𝑀𝐸�
a: Xét ΔABC vuông tại A và ΔDBE vuông tại D có
góc B chung
=>ΔABC đồng dạng với ΔDBE
=>AB/DB=AC/DE
=>AB*DE=AC*BD
b: BC=căn 18^2+24^2=30cm
BD=CD=30/2=15cm
ΔABC đồng dạng với ΔDBE
=>AB/DB=BC/BE=AC/DE
=>24/DE=30/BE=18/15=6/5
=>DE=20cm; BE=25cm
c: Xét ΔMAE vuông tại A và ΔMDC vuông tại D có
góc AME=góc DMC
=>ΔMAE đồng dạng với ΔMDC
=>MA/MD=ME/MC
=>MA*MC=MD*ME
d: MA/MD=ME/MC
=>MA/ME=MD/MC
=>ΔMAD đồng dạng với ΔMEC