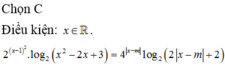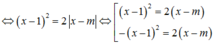phương trình 3^x=2x+1/4x+1 có bao nhiêu nghiệm thực

Những câu hỏi liên quan
Có bao nhiêu số nguyên m để phương trình
4
x
-
2
x
+
1
+
1
2
2
x
-
m
có đúng 2 nghiệm thực phân biệt A. 2 B. 3 C. 5 D. 4
Đọc tiếp
Có bao nhiêu số nguyên m để phương trình 4 x - 2 x + 1 + 1 = 2 2 x - m có đúng 2 nghiệm thực phân biệt
A. 2
B. 3
C. 5
D. 4
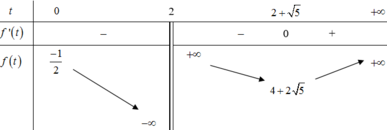
Đặt t = 2 x t > 0 phương trình trở thành:
![]()
Vẽ trên cùng hệ trục toạ độ hai parabol
P 1 : y = x 2 + 1 ; ( P 2 ) : y = - x 2 + 4 x - 1 .
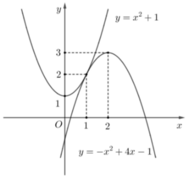
Với mỗi t > 0 cho ta một nghiệm x = log 2 t . Do đó phương trình có đúng 2 nghiệm thực phân biệt khi và chỉ khi hệ phương trình cuối có đúng 2 nghiệm dương phân biệt. Điều này tương đương với đường thẳng y = 2m cắt đồng thời (P1), (P2) tại đúng 2 điểm có hoành độ dương. Quan sát đồ thị suy ra các giá trị cần tìm của tham số là
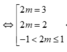
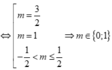
Chọn đáp án A.
Đúng 0
Bình luận (0)
Phương trình
1
2
log
3
(
x
+
3
)
+
1
2
log
9
(
x
-
1
)
4
2
log
9
(
4
x
)
có t...
Đọc tiếp
Phương trình 1 2 log 3 ( x + 3 ) + 1 2 log 9 ( x - 1 ) 4 = 2 log 9 ( 4 x ) có tất cả bao nhiêu nghiệm thực phân biệt ?
A. 1
B. 2
C. 3
D. 0
Bài 1: Phương trìnhlog_{2} ^3(x-1)-27y^3+8^y+1-x có bao nhiêu (x;y) nghiệm thuộc [8^{1992}; 8^{2020}]Bài 2: Tìm tập hợp số thực m để phương trình 2^{2x-1}+m×2^x+2m-20 có 2 nghiệm thực phân biệt thuộc đoạn [1;2]Bài 3: Tìm các số nguyên m để phương trình log_{dfrac{1}{2}}^{2} (x-2)^3+4(m-5) log _{dfrac{1}{2}}dfrac{1}{x-2}+4m-4 có nghiệm thuộc [dfrac{5}{2};4]Bài 4: Cho phương trình (m-2)×log_{2} ^2 (x-4)-(2m+1)log_{dfrac{1}{2}} (x-4)+m+20. Tìm m để phương trình có 2 nghiệm phân biệt x1, x2 thỏa mãn...
Đọc tiếp
Bài 1: Phương trình\(\log_{2} ^3(x-1)-27y^3+8^y+1-x\) có bao nhiêu \((x;y)\) nghiệm thuộc \([8^{1992}; 8^{2020}]\)
Bài 2: Tìm tập hợp số thực m để phương trình \(2^{2x-1}+m×2^x+2m-2=0\) có 2 nghiệm thực phân biệt thuộc đoạn [1;2]
Bài 3: Tìm các số nguyên m để phương trình \(\log_{\dfrac{1}{2}}^{2} (x-2)^3+4(m-5) log _{\dfrac{1}{2}}\dfrac{1}{x-2}+4m-4\) có nghiệm thuộc \([\dfrac{5}{2};4]\)
Bài 4: Cho phương trình \((m-2)×log_{2} ^2 (x-4)-(2m+1)log_{\dfrac{1}{2}} (x-4)+m+2=0.\) Tìm m để phương trình có 2 nghiệm phân biệt x1, x2 thỏa mãn 4<x1, x2<6
Cho phương trình
4
x
-
2
x
+
m
+
1
+
3
m
+
1
0
(
1
)
Biết rằng m là tham số thực sao cho 9m là số nguyên thỏa mãn
9
m
10
Có tất cả bao nhiêu giá trị m để phương trình (1...
Đọc tiếp
Cho phương trình 4 x - 2 x + m + 1 + 3 m + 1 = 0 ( 1 ) Biết rằng m là tham số thực sao cho 9m là số nguyên thỏa mãn 9 m < 10 Có tất cả bao nhiêu giá trị m để phương trình (1) có nghiệm duy nhất
A. 9
B. 10
C. 19
D. 20
Cho phương trình
2
x
-
1
2
.
log
2
x
2
-
2
x
+
3
4
x
-...
Đọc tiếp
Cho phương trình 2 x - 1 2 . log 2 x 2 - 2 x + 3 = 4 x - m log 2 2 x - m + 2 với m là tham số thực. Có bao nhiêu giá trị nguyên của m trên đoạn - 2019 ; 2019 để phương trình có đúng 2 nghiệm phân biệt.
A. 4036
B. 4034
C. 4038
D. 4040
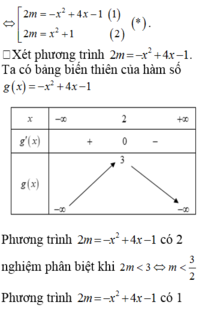
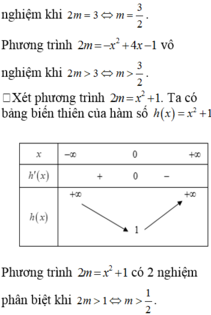
Cho phương trình \(x^2-2x-2\left|x-m\right|+1=0\) Có bao nhiêu giá trị của tham số m để có 3 nghiệm thực phân biệt
Gọi S là tập hợp các giá trị thực của tham số m để phương trình
4
x
-
m
.
2
x
+
2
m
+
1
0
có nghiệm. Tập RS có bao nhiêu giá trị nguyên? A.1 B.4 C.9 D.7
Đọc tiếp
Gọi S là tập hợp các giá trị thực của tham số m để phương trình 4 x - m . 2 x + 2 m + 1 = 0 có nghiệm. Tập R\S có bao nhiêu giá trị nguyên?
A.1
B.4
C.9
D.7
Gọi S là tập hợp các giá trị thực của tham số m để phương trình 4 x – m . 2 x + 2 m + 1 = 0 có nghiệm. Tập R\S có bao nhiêu giá trị nguyên
A. 1
B. 4
C. 9
D. 7
Nếu phương trình
4
x
−
m
.2
x
+
2
+
2
m
0
có hai nghiệm thực
x
1
,
x
2
thỏa mãn
x
1
+
x
2
3
thì m có giá trị bằng bao nhiêu?...
Đọc tiếp
Nếu phương trình 4 x − m .2 x + 2 + 2 m = 0 có hai nghiệm thực x 1 , x 2 thỏa mãn x 1 + x 2 = 3 thì m có giá trị bằng bao nhiêu?
A. m = 1
B. m = 2
C. m = 4
D. m = 8