Bài 3 (2,5 điểm): Cho 
ABC vuông tại A, trên tia BA lấy điểm D sao cho BD = BC. Kẻ DE 
BC ( E 
BC). Chứng minh
a, BAC = BED
b, ABE cân và AE // DC
c, Gọi M là trung điểm của DC. Chứng minh 3 đường thẳng AC, DE và BM đồng quy. (giúp mình vs )
Chứng minh AC, DE và BM đồng quy.
Theo giả thiết của đề bài, ta có:
ABC là tam giác vuông tại A.BD là đường cao của tam giác ABC.BD = BC.DE cắt AB và AC tại E và D, lần lượt.ABE là tam giác cân.AE // DC.M là trung điểm của đoạn DC.Ta cần chứng minh rằng AC, DE, và BM đồng quy, tức là chúng đồng quy tại một điểm duy nhất.
Để chứng minh điều này, ta sẽ dùng định lí Ceva trong tam giác ABC để chứng minh:
��.����.����=1BA.MCEM.ADCD=1
hay
����=����.����MCEM=CD.BCBAAD
Ta thấy rằng tam giác ABD và BDC đồng dạng, từ đó suy ra:
����=����BDCD=ADBC
Do BD là đường cao của ABC nên
��=��2��CD=ADBC2
Do đó:
����.����=����2��.����=��2��2CD.BCBAAD=ADBC2.BCBAAD=BC2AD2
Chú ý rằng ta có ��BE song song với ��DA nên trong tam giác ���,ADE, ta có
����=����=����MAEM=DABE=ADBA
Áp dụng hai công thức trên, ta có thể suy ra
����=��2��2.����=��.����2MCEM=BC2AD2.ADBA=BC2BA.AD
(công thức sao chép lần thứ hai trong phép tính trên cùng)
Tiếp theo, ta sẽ chứng minh
����=��2��2ECBE=AC2BA2
Áp dụng định lí phân giác trong tam giác ABC, ta có:
����=����.ECBE=ACBA.
Từ đó, suy ra:
����.����=��.����2.����=��2��2MCEM.ECBE=BC2BA.AD.ACBA=AC2BA2
Do đó, theo định lí Ceva, ta có AC, DE, và BM đồng quy. Vậy, ta đã chứng minh được điều cần chứng minh
a: Xét ΔBAC vuông tại A và ΔBED vuông tại E có
BC=BD
góc B chung
=>ΔBAC=ΔBED
b: ΔBAC=ΔBED
=>BA=BE
=>ΔABE cân tại B
Xet ΔBDC có BA/BD=BE/BC
nên AE//CD
c: ΔBDC cân tại B
mà BM là trung tuyến
nên BM vuông góc DC
=>BM,CA,DE đồng quy
Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm
a) Tính độ dài cạnh BC.
b) Trên tia BA lấy điểm D sao cho BD = BC. Kẻ DE vuông góc với BC tại E. Chứng minh tam giác BAC = tam giác BED.
c) Chứng minh tam giác ABE cân và AE song song DC.
d) Gọi M là trung điểm của AC. Hai đường thẳng AE và MD cắt nhau tại F. Chứng minh CF vuông góc với AC.
a) Áp dụng định lí Pytago vào \(\Delta ABC\)ta có:
\(BC^2=AB^2+AC^2\)Hay \(BC=\sqrt{6^2+8^2=10}\)
Ủng hộmi nha
a) Xét \(\Delta ABC\)vuông tại A, AB = 6cm; AC = 8cm
\(\Rightarrow BC^2=AB^2+AC^2\)
\(BC^2=6^2+8^2\)
\(BC^2=36+64\)
\(BC^2=100\)
\(BC=10\)
Suy ra cạnh BC = 10cm
b) Xét \(\Delta BAC\)và \(\Delta BED\)ta có:
\(\widehat{BAC}=\widehat{DEB}=90^o\)
\(\widehat{B}\)chung
\(BD=BC\left(gt\right)\)
\(\Rightarrow\Delta BAC=\Delta BED\)
Vậy...
Cho ∆ ABC vuông tại A có AB = 6cm, AC = 8cm.
a) Tính độ dài cạnh BC
b) Trên tia đối của tia AB lấy điểm D sao cho BD = BC, kẻ DE⊥BC tại E
(E ∈ BC). Chứng minh: ∆ BAC = ∆ BED
c) Chứng minh: AE // DC
d) Gọi M là trung điểm của AC. Hai đường thẳng AE và DM cắt nhau tại H.
Chứng minh: tam giác ACH vuông.
1. Cho ∆ABC vuông tại A (AB < AC). Vẽ tia BD là phân giác của góc ABC (D ∈ AC). Trên cạnh BC lấy điểm E sao cho BA = BE.
a. Chứng minh: ∆BAD = ∆BED
b. Từ A kẻ AH ⊥ BC tại H. Chứng minh: AH // DE
c. Trên tia đối của tia ED lấy điểm K sao cho ED = EK. Chứng minh: Góc EKC = góc ABC
2.
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE = BA. Phân giác góc B cắt AC tại D.
a. Chứng minh ∆ABD = Đồng ý∆EBD và DE ⊥ BC
b. Gọi K là giao điểm của tia ED và tia BA. Chứng minh AK = EC.
c. Gọi M là trung điểm của KC. Chứng minh ba điểm B, D, M thẳng hàng.
3.
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm M sao cho BA = BM. Gọi E là trung điểm AM.
a.Chứng minh: ∆ABE = ∆MBE.
b. Gọi K là giao điểm BE và AC. Chứng minh: KM ⊥ BC,
c. Qua M vẽ đường thẳng song song với AC cắt BK tại F. Trên đoạn thẳng KC lấy điểm Q sao cho KQ = MF. Chứng minh: góc ABK = QMC
4
Cho tam giác ABC có AB = AC, lấy M là trung điểm của BC.
a) Chứng minh ∆ABM = ∆ACM
b) Kẻ ME ⊥ AB tại Em kẻ MF ⊥ AC tại F. Chứng minh AE = AF.
c) Gọi K là trung điểm của EF. Chứng minh ba điểm A, K, M thẳng hàng
d) Từ C kẻ đương thẳng song song với AM cắt tia BA tại D. Chứng minh A là trung điểm của BD.
4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng
4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng
\(Bài 1. Cho góc xOy, có Ot là tia phân giác. Lấy điểm A trên tia Ox, điểm B trên tia Oy sao cho OA = OB. Vẽ đoạn thẳng AB cắt Ot tại M. Chứng minh a) OAM = OBM; b) AM = BM; OM AB c) OM là đường trung trực của AB d) Trên tia Ot lấy điểm N . Chứng minh NA = NB Bài 2. Cho ABC vuông tại A, trên tia đối của tia CA lấy điểm K sao cho CK = CA, từ K kẻ KE vuông góc với đường thẳng AC. Chứng mỉnhằng: a) AB // KE b) ABC = KEC ; BC = CE Bài 3. Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C. Trên tia Oy lấy hai điểm B,D sao cho OA = OB, AC = BD. a) Chứng minh: AD = BC. b) Gọi E là giao điểm AD và BC. Chứng minh: EAC = EBD c) Chứng minh: OE là phân giác của góc xOy, OE CD Bài 4. Cho ABC coù BÂ=900, gọi M là trung điểm của BC. Trên tia đối của tia AM lấy điểm E sao cho ME = MA. a) Tính BCE b) Chứng minh BE // AC. Bài 5. Cho ABC, lấy điểm D thuộc cạnh BC ( D không trùng với B,C). Gọi Mlà trung điểm của AD. Trên tia đối của tia MB lấy điểm E sao cho ME= MB, trên tia đối của tia MC lấy điểm F sao cho MF= MC. Chứng minh rằng: a) AME = DMB; AE // BC b) Ba điểm E, A, F thẳng hàng c) BF // CE Bài 6: Cho có B = C , kẻ AH BC, H BC . Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh: a) AB = AC b) ABD = ACE c) ACD = ABE d) AH là tia phân giác của góc DAE e) Kẻ BK AD, CI AE. Chứng minh ba đường thẳng AH, BK, CI cùng đi qua một điểm. \)
chịu. nhình rối hết cả mắt @-@
Cho tam giác ABC vuông tại A có AB = 6cm , AC = 8 cm .
a) tính độ dài BC
b) trên tia BA lấy điểm D sao cho BD = BC. Nối D với C , vẽ DE vuông góc với BC ( E thuộc BC ) chứng minh △BAC = △BED
c) chứng minh △ABE cân và AE // DC
a: BC=10cm
b: Xét ΔBAC vuông tại A và ΔBED vuông tại E có
BC=BD
\(\widehat{EBD}\) chung
Do đó: ΔBAC=ΔBED
c: Ta có: ΔBAC=ΔBED
nên BA=BE
hay ΔBAE cân tại B
Xét ΔBCD có BA/BD=BE/BC
nên AE//DC
Cho tam giác ABC vuông tại A . Tia phân giác của góc B cắt AC ở D, E là điểm trên cạnh BC sao cho BE = BA .
a) gọi F là giao điểm của DE và AB . chứng minh rằng DC = DF
b) Chứng minh AD< DC
c) Chứng minh BD là đường trung trực của AE và AE // FC
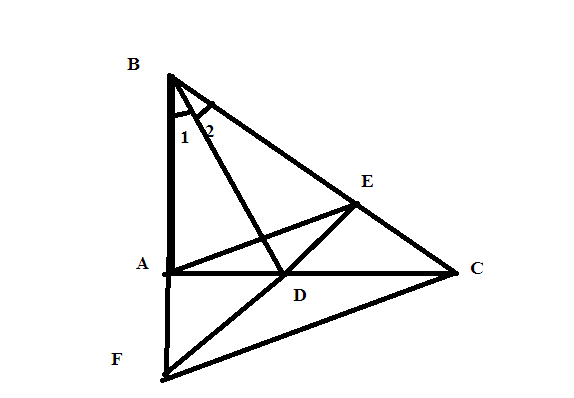
Xét ΔBAD và ΔBDE có:
BD là cạnh chung
B1=B2 (BD là tia phân giác của \(\widehat{B}\))
BA = BE (GT)
Nên ΔBAD= ΔBDE (c.g.c)
=>\(\widehat{ADB}=\widehat{BDE}\)
Ta có:\(\widehat{ADB}+\widehat{ADF}=\widehat{BDF}\)
\(\widehat{BDE}+\widehat{EDC}=\widehat{BDC}\)
Mà :\(\widehat{ADB}=\widehat{BDE}\)(CMT)
\(\widehat{ADF}=\widehat{EDC}\)( 2 góc đối đỉnh)
=>\(\widehat{BDF}=\widehat{BDC}\)
Xét ΔBDF và Δ BDC, có:
\(\widehat{BDF}=\widehat{BDC}\)
BD là cạnh chung
B1=B2
Nên ΔBDF=ΔBDC (g.c.g)
=>DC = DF
b)Ta có:ΔEDC vuông tại E=> DC là cạnh lớn nhất hay DC>DE
MÀ DE=AD (ΔBAD và ΔBDE)
=> AD< DC
c) Ta có BE=BA=>ΔBEA cân tại B
Mà BD là tia phân giác=>BD là đường trung trực
Vì :ΔBDF=ΔBDC=>BF=BC
=>ΔBFC cân tại B=>\(\widehat{C}=\widehat{F}\)
Ta có:\(\widehat{B}+\widehat{C}+\widehat{F}=180^o\)
=>\(\widehat{B}+\widehat{C}.2=180^O\)
=>\(\widehat{C}=\dfrac{180^O-\widehat{B}}{2}\)(1)
vÌ ΔBAE cân tại B
Tương tự ta có:
\(\widehat{E}=\dfrac{180^o-\widehat{B}}{2}\)(2)
Từ (1) và (2)=> \(\widehat{E}=\widehat{C}\)
Mà 2 góc này ở vị trí đồng vị=>AE // FC
Bài 1. Cho tam giác ABC cân tại A ( góc A< 90°). Kẻ BD vuông góc với AC tại D, kẻ CE vuông góc vói AB tại E.
a) Chứng minh tam giác ADE cân.
b) Chứng minh DE// BC.
c) Gọi I là giao điểm của BD và CE. Chứng minh IB = IC
d) Chứng minh. AI vuông góc BC.
Bài 2. Cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy điểm D trên tia đối của tia CA lấy điểm E sao cho BD = CE, Gọi I là giao điểm của BE và CD.
a) Chứng minh IB = IC, ID = IE.
b) Chứng minh DE // BC.
c) Gọi M là trung điểm của BC. Chứng minh ba điểm A, M, I thẳng hàng
Cho tam giác ABC có AB=AC=5cm, BC=8cm. Kẻ AH vuông góc với BC (H thuộc BC)
a, Chứng minh: HB=HC và BAH=CAH
b, Tính độ dài AH
c, Kẻ HD vuông góc với AB (D thuộc AB) , kẻ HE vuông góc với AC (E thuộc AC). Chứng minh tam giác HDE là tam giác cân
Bài 3: Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của CB lấy N sao cho BM=CN
a, Chứng minh: tam giác ABM = tam giác ACN
b, Kẻ BH vuông góc với AM, CK vuông góc với AN( H thuộc AM,K thuộc AN). Chứng minh : AH=AK
c, Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao?
Bài 4: Cho tam giác ABC, kẻ BE vuông góc với AC và CF vuông góc với AB. Biết BE=CF=8 cm. Độ dài các đoạn thẳng BF và BC tỉ lệ với 3 và 5.
a, Chứng minh tam giác ABC là tam giác cân
b, Tính độ dài cạnh đáy BC
c, BE và CF cắt nhau tại O. Nối OA và EF. Chứng minh đường thẳng OA là trung trực của đoạn thẳng EF
Bài 5 : Cho tam giác ABC vuông tại A, BD là tia phân giác của góc ABC (D thuộc AC). Từ D kẻ DE vuông góc với BC tại E. Gọi I là giao điểm của AE và BD. Chứng minh:
a, Tam giác ADB= tam giác EDB
b, BD là đường trung trực của AE
c, Tam giác EDC vuông cân
d, Lấy F thuộc tia đối của tia AB sao cho AF=EC.Chứng minh 3 điểm E, D, F thẳng hàng
Bài 6: Cho tam giác MNP cân tại M. Trên cạnh MN lấy điểm E, trên cạnh MP lấy điểm F sao cho ME=MF. Gọi S là giao điểm của NF và PE. Chứng minh
a, Tam giác MNF= tam giác MPE
b, Tam giác NSE= tam giác PSE
c, EF // NP
d, Lấy K là trung điểm của NP. Chứng minh ba điểm M, S, K thẳng hàng
Bài 7: Cho tam giác ABC vuông tại A. Trên BC lấy E sao cho BE=AB. Qua E kẻ đường thẳng vuông góc với BC cắt AC tại D
a, Chứng minh AD=AE và góc ABD= góc EBD
b, Lấy điểm F thuộc tia đối của tia AB sao cho AF=EC. Chứng minh tam giác DFC cân
c, Gọi O là giao điểm của BD và AE. Chứng minh BD là đường trung trực của AE
d, Chứng minh 3 điểm F, D,E thẳng hàng
Mình đang cần gấp
Bài 3:
a: Xét ΔABM và ΔACN có
AB=AC
góc ABM=góc ACN
BM=CN
Do đó: ΔABM=ΔACN
Suy ra: AM=AN
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH=góc CAK
Do đó; ΔAHB=ΔAKC
Suy ra: AH=AK và BH=CK
c: Xét ΔHBM vuông tại H và ΔKCN vuông tại K có
MB=CN
góc M=góc N
Do đó ΔHBM=ΔKCN
Suy ra: góc HBM=góc KCN
=>góc OBC=góc OCB
hay ΔOBC can tại O
