Các câu hỏi tương tự
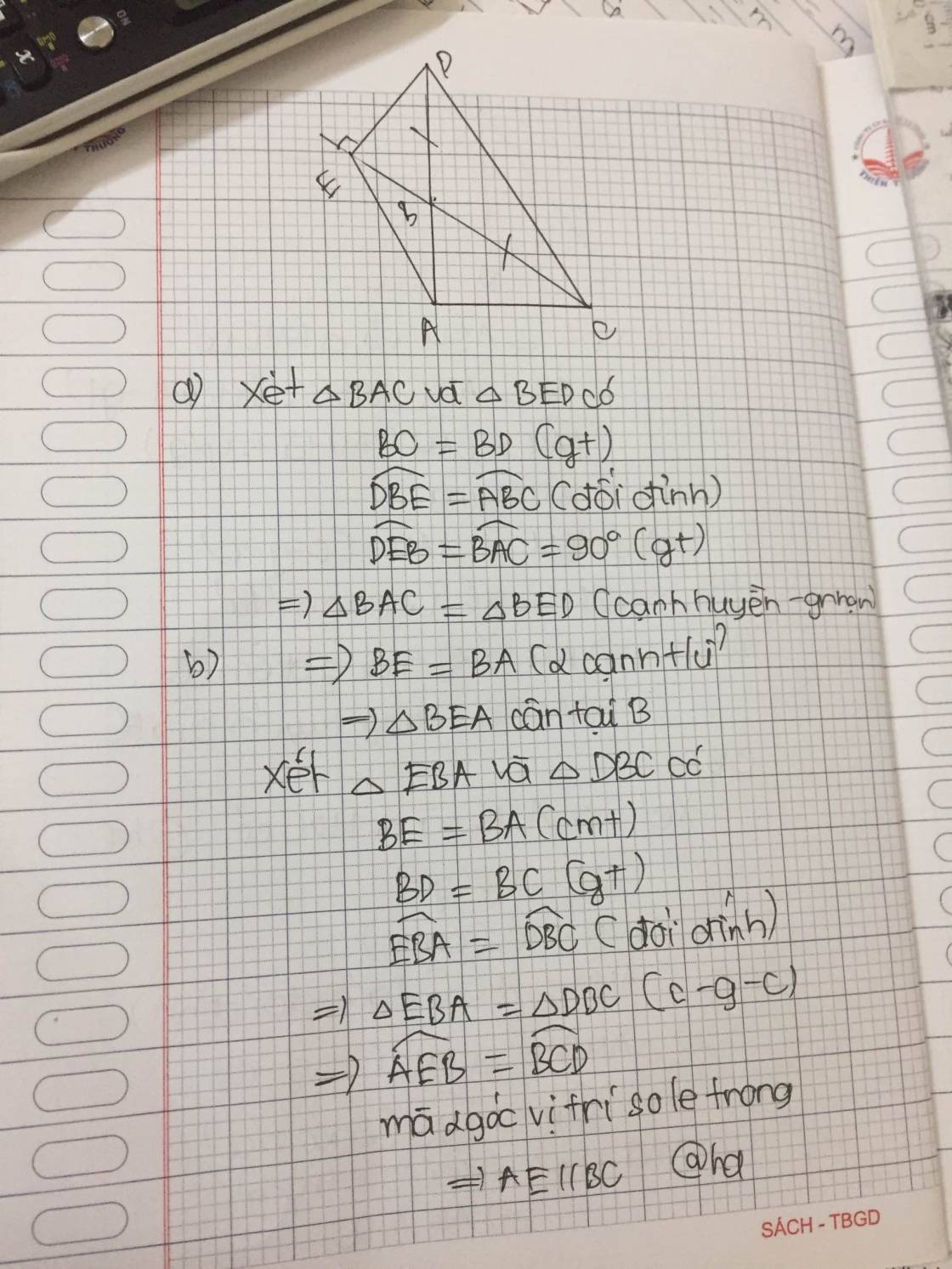
Bài 3 (2,5 điểm): Cho ABC vuông tại A, trên tia BA lấy điểm D sao cho BD BC. Kẻ DE BC ( E BC). Chứng minha, BAC BEDb, ABE cân và AE // DCc, Gọi M là trung điểm của DC. Chứng minh 3 đường thẳng AC, DE và BM đồng quy. (giúp mình vs )
Đọc tiếp
Bài 3 (2,5 điểm): Cho ![]() ABC vuông tại A, trên tia BA lấy điểm D sao cho BD = BC. Kẻ DE
ABC vuông tại A, trên tia BA lấy điểm D sao cho BD = BC. Kẻ DE ![]() BC ( E
BC ( E ![]() BC). Chứng minh
BC). Chứng minh
a, ![]() BAC =
BAC = ![]() BED
BED
b, ![]() ABE cân và AE // DC
ABE cân và AE // DC
c, Gọi M là trung điểm của DC. Chứng minh 3 đường thẳng AC, DE và BM đồng quy. (giúp mình vs )
Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm
a) Tính độ dài cạnh BC.
b) Trên tia BA lấy điểm D sao cho BD = BC. Kẻ DE vuông góc với BC tại E. Chứng minh tam giác BAC = tam giác BED.
c) Chứng minh tam giác ABE cân và AE song song DC.
d) Gọi M là trung điểm của AC. Hai đường thẳng AE và MD cắt nhau tại F. Chứng minh CF vuông góc với AC.
1. Cho ∆ABC vuông tại A (AB AC). Vẽ tia BD là phân giác của góc ABC (D ∈ AC). Trên cạnh BC lấy điểm E sao cho BA BE.a. Chứng minh: ∆BAD ∆BEDb. Từ A kẻ AH ⊥ BC tại H. Chứng minh: AH // DEc. Trên tia đối của tia ED lấy điểm K sao cho ED EK. Chứng minh: Góc EKC góc ABC2.Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE BA. Phân giác góc B cắt AC tại D. a. Chứng minh ∆ABD Đồng ý∆EBD và DE ⊥ BCb. Gọi K là giao điểm của tia ED và tia BA. Chứng minh AK EC.c. Gọi M là trung điểm c...
Đọc tiếp
1. Cho ∆ABC vuông tại A (AB < AC). Vẽ tia BD là phân giác của góc ABC (D ∈ AC). Trên cạnh BC lấy điểm E sao cho BA = BE.
a. Chứng minh: ∆BAD = ∆BED
b. Từ A kẻ AH ⊥ BC tại H. Chứng minh: AH // DE
c. Trên tia đối của tia ED lấy điểm K sao cho ED = EK. Chứng minh: Góc EKC = góc ABC
2.
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE = BA. Phân giác góc B cắt AC tại D.
a. Chứng minh ∆ABD = Đồng ý∆EBD và DE ⊥ BC
b. Gọi K là giao điểm của tia ED và tia BA. Chứng minh AK = EC.
c. Gọi M là trung điểm của KC. Chứng minh ba điểm B, D, M thẳng hàng.
3.
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm M sao cho BA = BM. Gọi E là trung điểm AM.
a.Chứng minh: ∆ABE = ∆MBE.
b. Gọi K là giao điểm BE và AC. Chứng minh: KM ⊥ BC,
c. Qua M vẽ đường thẳng song song với AC cắt BK tại F. Trên đoạn thẳng KC lấy điểm Q sao cho KQ = MF. Chứng minh: góc ABK = QMC
4
Cho tam giác ABC có AB = AC, lấy M là trung điểm của BC.
a) Chứng minh ∆ABM = ∆ACM
b) Kẻ ME ⊥ AB tại Em kẻ MF ⊥ AC tại F. Chứng minh AE = AF.
c) Gọi K là trung điểm của EF. Chứng minh ba điểm A, K, M thẳng hàng
d) Từ C kẻ đương thẳng song song với AM cắt tia BA tại D. Chứng minh A là trung điểm của BD.
Cho ∆ ABC vuông tại A có AB = 6cm, AC = 8cm.
a) Tính độ dài cạnh BC
b) Trên tia đối của tia AB lấy điểm D sao cho BD = BC, kẻ DE⊥BC tại E
(E ∈ BC). Chứng minh: ∆ BAC = ∆ BED
c) Chứng minh: AE // DC
d) Gọi M là trung điểm của AC. Hai đường thẳng AE và DM cắt nhau tại H.
Chứng minh: tam giác ACH vuông.
Cho tam giác ABC vuông tại A có AB = 6cm , AC = 8 cm .
a) tính độ dài BC
b) trên tia BA lấy điểm D sao cho BD = BC. Nối D với C , vẽ DE vuông góc với BC ( E thuộc BC ) chứng minh △BAC = △BED
c) chứng minh △ABE cân và AE // DC
Cho tam giác ABC vuông tại A . Tia phân giác của góc B cắt AC ở D, E là điểm trên cạnh BC sao cho BE = BA .
a) gọi F là giao điểm của DE và AB . chứng minh rằng DC = DF
b) Chứng minh AD< DC
c) Chứng minh BD là đường trung trực của AE và AE // FC
Bài 1: Cho tam giác vuông ABC, góc A 90o, phân giác BD. Kẻ BD vuông góc BC tại E. Trên tia đối của tia AB lấy điểm F sao cho AF CE. Chứng minh rằng:a) BD là đường trung trực của AE.b) ADDCc) Ba điểm E, D, F thẳng hàngBài 2: Cho tam giác vuông ABC, góc A 90o , AB 6cm, AC 8cm.a) Tính BCb) Trung trực của BC cắt AC tại D và cắt AB tại F. Chứng minh góc DBC góc DCBc) Trên tia đối của tia DB lấy điểm E sao cho DEDC. Chứng minh tam giác BCE vuôngd)Chứng minh:DF là phân giác của góc ADE và BE vuôn...
Đọc tiếp
Bài 1: Cho tam giác vuông ABC, góc A = 90o, phân giác BD. Kẻ BD vuông góc BC tại E. Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chứng minh rằng:
a) BD là đường trung trực của AE.
b) AD<DC
c) Ba điểm E, D, F thẳng hàng
Bài 2: Cho tam giác vuông ABC, góc A = 90o , AB = 6cm, AC = 8cm.
a) Tính BC
b) Trung trực của BC cắt AC tại D và cắt AB tại F. Chứng minh góc DBC = góc DCB
c) Trên tia đối của tia DB lấy điểm E sao cho DE=DC. Chứng minh tam giác BCE vuông
d)Chứng minh:DF là phân giác của góc ADE và BE vuông góc CF
Bải 3: Cho tam giác đều ABC. Tia phân giác góc B cắt cạnh AC ở M. Từ A kẻ đường thẳng vuông góc với AB cắt các tia BM, BC lần lượt ở M và E. Chứng minh:
a) Tam giác ANC là tam giác cân
b) NC vuông góc BC
c) Tam giác AEC là tam giác cân
d) So sánh BC và NE
Bài 4: Cho tam giác nhọn ABC, kẻ BM vuông góc AC, CN vuông góc AB. Trên tia đối của tia BM lấy điểm D sao cho BD=AC, trên tia đối của tia CN lấy điểm E sao cho CE=AB. Chứng minh:
a) Góc ACE= góc ABD
b) Tam giác ABD = tam giác ECA
c) Tam giác AED là tam giác vuông cân
Bài 1 : Cho tam giác ABC cân tại A . Trên tia đối của tia BA , lấy điểm D ; trên tia đối của tia CA lấy điểm E sao cho BD CE . Gọi I là giao điểm của BE và CD .a) Chứng minh IB IC và ID IEb) Chứng minh BC // DE c) Gọi M là trung điểm của BC . Chứng minh ba điểm A, M, I thẳng hàng . Bài 2 : Cho tam giác ADE cân tại A . Trên cạnh DE lấy điểm B và C sao cho DB EC ( BD ; Ec 1/2 DE ) a) Tam giác ABC là tam giác gì ? Vì sao ? b) Kẻ BM vuông góc với AD ; CN vuông góc với AE . Chứng minh BM CN c...
Đọc tiếp
Bài 1 : Cho tam giác ABC cân tại A . Trên tia đối của tia BA , lấy điểm D ; trên tia đối của tia CA lấy điểm E sao cho BD = CE . Gọi I là giao điểm của BE và CD .
a) Chứng minh IB = IC và ID = IE
b) Chứng minh BC // DE
c) Gọi M là trung điểm của BC . Chứng minh ba điểm A, M, I thẳng hàng .
Bài 2 : Cho tam giác ADE cân tại A . Trên cạnh DE lấy điểm B và C sao cho DB = EC ( BD ; Ec < 1/2 DE )
a) Tam giác ABC là tam giác gì ? Vì sao ?
b) Kẻ BM vuông góc với AD ; CN vuông góc với AE . Chứng minh BM = CN
c) Gọi I là giao điểm của BM và CN . Tam giác IBC là tam giác gì ? Vì sao ?
d) Chứng minh AI là tia phân giác của góc BAC .
Câu 1: Cho tam giác ABC có góc A 90 độ. kẻ AH vuông góc với BC (H e BC) Trên đường vuông góc với BC tại điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho AHBD chứng minh a) tam giác AHBDBH b) hai đường thẳng AB và DH có song song không? vì sao?Câu 2: Cho góc nhọn xOy. Trên tia Ox lấy điểm A, lấy điểm B trên tia Oy sao cho OAOB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho ACBD chứng minh ADBC. gọi E là giao điểm AD và BC, chứng minh tam giác EADEBD.Câu 3: Cho tam giác ABC vuông...
Đọc tiếp
Câu 1: Cho tam giác ABC có góc A= 90 độ. kẻ AH vuông góc với BC (H e BC) Trên đường vuông góc với BC tại điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho AH=BD chứng minh a) tam giác AHB=DBH b) hai đường thẳng AB và DH có song song không? vì sao?
Câu 2: Cho góc nhọn xOy. Trên tia Ox lấy điểm A, lấy điểm B trên tia Oy sao cho OA=OB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho AC=BD chứng minh AD=BC. gọi E là giao điểm AD và BC, chứng minh tam giác EAD=EBD.
Câu 3: Cho tam giác ABC vuông tại A, kẻ phân giác BD (D e AC), kẻ DE vuông góc với BC tại E. Chứng minh BA=BE
Câu 4: Cho tam giác ABC vuông tại A, kẻ phân giác BD (D e AC), kẻ DE vuông góc với BC tại E. gọi F là giao điểm của tia BA và ED. chứng minh tam giác BDA=BDE và DC=DF
Giúp mình giải lun nhé. Giúp mình đi mình Tick cho!!!