Cho △ A B C có B ^ + C ^ = 90 o . Khi đó tam giác ABC là:
A. Tam giác đều
B. Tam giác vuông
C. Tam giác cân
D. Tam giác vuông cân
Cho tam giác nhọn ABC. Đường cao BD và CE cắt tại nhau tại H. Trên BD lấy điểm M sao cho góc MAC = 90o ; Trên CE lấy điểm N sao cho góc ANB = 90o . Chứng minh: AM = AN.
Cho tam giác ABC, M là trung điểm của BC
CMR: a, Nếu AM=BC/2 thì góc A=90o
b, Nếu góc A=90o thì AM=BC/2
Cho tam giác ABC có ∠A=90o, kẻ AH vuông góc với BC (H thuộc BC). Các tia phân giác của ∠C và ∠BAH cắt nhau ở I. Chứng minh rằng: ∠(AIC)=90o
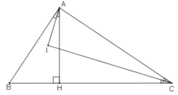
Ta có: AH⊥BC (gt) ⇒ ΔAHB vuông tại H
Trong tam giác vuông AHB ta có: ∠BHA = 90o
⇒ ∠B + ∠BAH = 90o (1)
Trong tam giác vuông ABC ta có: ∠BAC = 90o
⇒ ∠B + ∠C = 90o (2)
Từ (1) và (2) suy ra: ∠BAH = ∠C (3)
+) Vì AI là tia phân giác của góc BAC nên:
∠(BAI) = ∠(IAH) = 1/2.∠BAH (4)
Do CI là tia phân giác của góc ACB nên:
∠(ACI) = ∠(ICB) = 1/2.∠C (5)
+) Từ (3); (4) và (5) suy ra:
∠(BAI) = ∠(IAH) = ∠(ACI) = ∠(ICB)
+) Lại có:
∠BAI + ∠IAC = 90º
Suy ra: ∠ICA + ∠IAC = 90º
Trong ΔAIC có: ∠ICA+ ∠IAC = 90º
Vậy: ∠AIC = 90º.
Cho tam giác ABC có A ^ = 90 o ;AB=AC. Khi đó:
A. ΔABC là tam giác vuông
B. ΔABC là tam giác cân
C. ΔABC là tam giác vuông cân
D. Cả A,B,C đều đúng
Cho tam giác ABC có A ^ = 90 o , B ^ = C ^ . Tính số đo góc B
A. 90 °
B. 90 °
C. 90 °
D. 90 °
Cho △ABC : Góc A = 90o, \(\dfrac{AB}{AC}=\dfrac{5}{7}\), AH = 15cm . Tính HB, HC
Xét tam giác ABH và ACH
=> 2 tam giác trên đồng dạng
=> \(\dfrac{AH}{HC}=\dfrac{AB}{AC}\)
\(mà\dfrac{AB}{AC}=\dfrac{5}{7}=>\dfrac{AH}{HC}=\dfrac{5}{7}=>HC=\dfrac{7.15}{5}=21\left(cm\right)\)
Áp dụng hệ thức lượng :
AH^2 = HB.HC => HB = \(\dfrac{15^2}{21}=\dfrac{75}{7}\left(cm\right)\)
*Đề bài viết thiếu đường cao AH :v
Xét tam giác AHB và tam giác CHA có:
góc AHB = góc CHA = 90o
góc BAH = góc C ( cùng phụ với góc B)
⇒\(\dfrac{AH}{HC}=\dfrac{AB}{AC}=\dfrac{HB}{AH}\)
Theo đề bài ta có : \(\dfrac{AB}{AC}=\dfrac{5}{7}\)
⇒\(\dfrac{AB}{AC}=\dfrac{HB}{AH}\Leftrightarrow\dfrac{5}{7}=\dfrac{HB}{15}\Leftrightarrow HB=\dfrac{75}{7}\left(cm\right)\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AH}{HC}\Leftrightarrow\dfrac{5}{7}=\dfrac{15}{HC}\Leftrightarrow HC=21\left(cm\right)\)
Cho tam giác ABC có ∠ A = 90 o , ∠ B = 30 o . Cạnh lớn nhất của tam giác là:
A. Cạnh AB
B. Cạnh BC.
C. Cạnh CA
D. AB và CA
Tam giác ABC là tam giác vuông nên góc A là góc lớn nhất, suy ra cạnh lớn nhất là BC. Chọn B
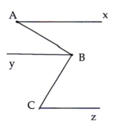
Cho hình vẽ bên, biết: x A B ^ = 30 O , A B C ^ = 90 O , By //Cz //Ax. Tính số đo B C z ^ .
Cho tam giác ABC có đường cao AH. Chứng minh nếu AH2=HB.HC thì BAC=90o
Ta có: \(AH^2=HB.HC\Rightarrow\dfrac{AH}{HB}=\dfrac{HC}{AH}\)
Xét tam giác AHB và tam giác CHA có:
\(\widehat{AHB}=\widehat{AHC}=90^0\)
\(\dfrac{AH}{HB}=\dfrac{HC}{AH}\)
\(\Rightarrow\Delta AHB\sim\Delta CHA\left(c.g.c\right)\)
\(\Rightarrow\widehat{BAH}=\widehat{HCA}\)
Mà \(\widehat{HCA}+\widehat{HAC}=90^0\)(ΔHAC vuông tại H)
\(\Rightarrow\widehat{BAH}+\widehat{HAC}=90^0\)
\(\Rightarrow\widehat{BAC}=90^0\left(đpcm\right)\)
