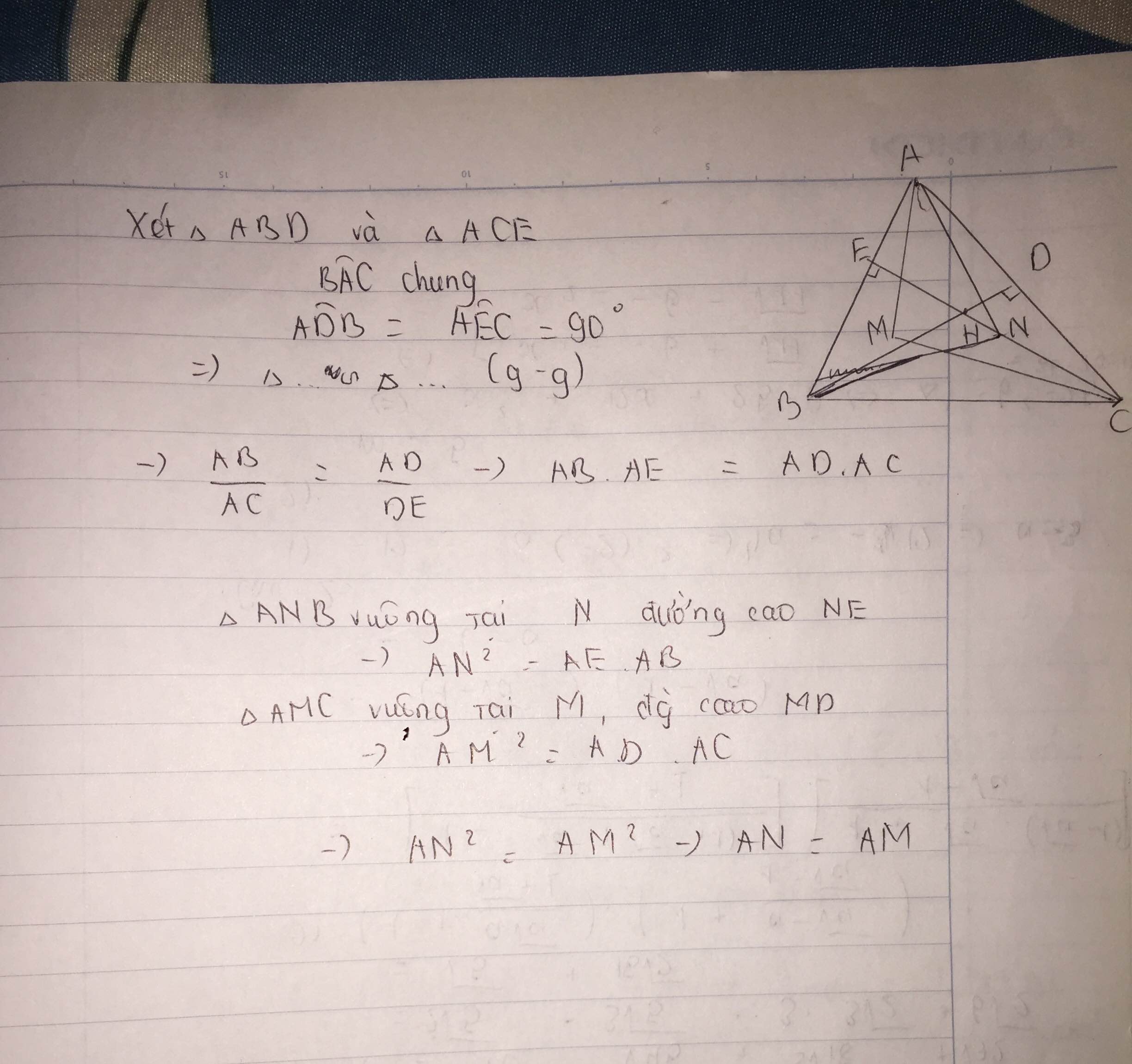Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
cho tam giác ABC có 3 góc nhọn . các đường cao BD ,CE cắt nhau tại H
1/ CMR : tam giác ADB ∞ tam giác AEC
2/ CMR : HB.HD=HC.HE
3/ trên các đoạn thẳng BD và CE lấy lần lượt 2 điểm M , N sao cho ∠AMC =∠ANB = 90o .CMR: AM=AN
cho tam giác ABC nhọn các đường cao BD và CE cắt nhau tại H
1 chứng minh tam giác ABC ffongf dạng với tam giác ACE và AB.AE=AC.AD
2 chứng minh góc ADE \ góc ABC
3 trên các đoạn thẳng BD và CE lấy lần lượt hai điểm M và N sao cho góc AMC = goác ANB = 90 đọ . Chứng minh AM2 = AC,AD và AM \ AN
cho tam giác nhọn ABC, các đường cao BD, CE cắt nhau tại H. trên các đoạn HB, HC lấy các điểm M, N sao cho góc AMC = góc ANB = 90 độ. chứng minh:
a) AM= AD.AC
b) Tam giác AMN là tam giác cân
Cho tam giác ABC có 3 góc nhọn, đường cao BD và CE. Trên đoạn BD lấy M sao cho góc AMC bằng 90 độ. Trên đoạn CE lấy N sao cho góc ANB = 90 độ. Chứng minh AM=AN.
Cho tam giác ABC có các góc đều nhọn. Đường cao BD, CEcắt nhau tại H. Trên các đoạn thẳng BD và CE lấy lần lượt hai điểm M và N sao cho góc A MC =ANC = 90°. Chứng minh rằng AM = AN
Cho tam giác nhọn ABC, hai đường cao BD và CE cắt nhau tại H, Trên HB và HC lần lượt lất các điểm M và N sao cho góc AMC = góc ANB = 90 độ. CMR: AM = AN
cho tam giác abc có ba goc nhỏ hơn 90 độ. các đường cao bd và ce cắt nhau tại h. a, chứng minh tam giác abc đồng dạng với tam giác ace. b, chứng minh hb.hd=hd.he. c, trên các đoạn thẳng bd và ce lấy lần lượt 2 điểm m và n sao cho góc amc= góc anb=90 độ. chứng minh rằng am=an
Cho tam giác ABC nhọn(AB<AC) có hai đường cao BD và CE cắt nhau tại H
a. chứng minh tam giác ABD đồng dạng với tam giác ACE
b. chứng minh HD.HB=HE.HC
c.AH cắt BC tại F. Kẻ FI vuông góc AC tại I. Trên tia đối tia AF lấy điểm N sao cho AN=AF.Gọi M là TRung điểm cạnh IC. chứng minh NI vuông góc vs FM
Cho tam giác ABC cân tại A. Kẻ BD vuông góc với AC, CE vuông góc với AB. BD và CE cắt nhau tại H. Chứng minh:
a, Tam giác ABD = tam giác ACE.
b, Tam giác BHC cân.
c, ED // BC
d, AH cắt BC tại K, trên HK lấy M sao cho K là trung điểm của HM. Chứng minh tam giác ACM vuông.