Đinh Phương Linh tham khảo nha:

 2sin²2x + sin7x - 1 = sinx <=> sin7x - sinx - cos4x = 0 
<=> 2cos4x.sin3x - cos4x = 0 <=> cos4x.(2sin3x -1) = 0 

<=> [ cos4x = 0 
----- [ sin3x = 1/2 

<=> [ x = pi/8 + kpi/4 
----- [ x = pi/18 + 2kpi/3 
----- [ x = 5pi/18 + 2kpi 

\(A=\frac{2047}{1024}\)

\(a,1+tan^2x=\dfrac{1}{cos^2x}\\ VT=1+\dfrac{sin^2x}{cos^2x}\\ =\dfrac{cos^2x}{cos^2x}+\dfrac{sin^2x}{cos^2x}\\ =\dfrac{sin^2x+cos^2x}{cos^2x}=\dfrac{1}{cos^2x}=VP\)

\(b,VT=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}\\ =\dfrac{sin^2x+cos^2x}{cosx.sinx}=\dfrac{1}{cosx.sinx}=VP\)

1: \(y=x+\dfrac{4}{\left(x-2\right)^2}\)

\(\Leftrightarrow y'=1+\left(\dfrac{4}{\left(x-2\right)^2}\right)'\)

=>\(y'=1+\dfrac{4'\left(x-2\right)^2-4\left[\left(x-2\right)^2\right]'}{\left(x-2\right)^4}\)

=>\(y'=1+\dfrac{-4\cdot2\cdot\left(x-2\right)'\left(x-2\right)}{\left(x-2\right)^4}\)

=>\(y'=1-\dfrac{8}{\left(x-2\right)^3}\)

Đặt y'=0

=>\(\dfrac{8}{\left(x-2\right)^3}=1\)

=>\(\left(x-2\right)^3=8\)

=>x-2=2

=>x=4

Đặt \(f\left(x\right)=x+\dfrac{4}{\left(x-2\right)^2}\)

\(f\left(4\right)=4+\dfrac{4}{\left(4-2\right)^2}=4+1=5\)

\(f\left(0\right)=0+\dfrac{4}{\left(0-2\right)^2}=0+\dfrac{4}{4}=1\)

\(f\left(5\right)=5+\dfrac{4}{\left(5-2\right)^2}=5+\dfrac{4}{9}=\dfrac{49}{9}\)

Vì f(0)<f(4)<f(5)

nên \(f\left(x\right)_{max\left[0;5\right]\backslash\left\{2\right\}}=f\left(5\right)=\dfrac{49}{9}\) và \(f\left(x\right)_{min\left[0;5\right]\backslash\left\{2\right\}}=1\)

2: \(y=cos^22x-sinx\cdot cosx+4\)

\(=1-sin^22x-\dfrac{1}{2}\cdot sin2x+4\)

\(=-sin^22x-\dfrac{1}{2}\cdot sin2x+5\)

\(=-\left(sin^22x+\dfrac{1}{2}\cdot sin2x-5\right)\)

\(=-\left(sin^22x+2\cdot sin2x\cdot\dfrac{1}{4}+\dfrac{1}{16}-\dfrac{81}{16}\right)\)

\(=-\left(sin2x+\dfrac{1}{4}\right)^2+\dfrac{81}{16}\)

\(-1< =sin2x< =1\)

=>\(-\dfrac{3}{4}< =sin2x+\dfrac{1}{4}< =\dfrac{5}{4}\)

=>\(0< =\left(sin2x+\dfrac{1}{4}\right)^2< =\dfrac{25}{16}\)

=>\(0>=-\left(sin2x+\dfrac{1}{4}\right)^2>=-\dfrac{25}{16}\)

=>\(\dfrac{81}{16}>=-sin\left(2x+\dfrac{1}{4}\right)^2+\dfrac{81}{16}>=-\dfrac{25}{16}+\dfrac{81}{16}=\dfrac{7}{2}\)

=>\(\dfrac{81}{16}>=y>=\dfrac{7}{2}\) 

\(y_{min}=\dfrac{7}{2}\) khi \(sin2x+\dfrac{1}{4}=\dfrac{5}{4}\)

=>\(sin2x=1\)

=>\(2x=\dfrac{\Omega}{2}+k2\Omega\)

=>\(x=\dfrac{\Omega}{4}+k\Omega\)

\(y_{max}=\dfrac{81}{16}\) khi sin 2x=-1

=>\(2x=-\dfrac{\Omega}{2}+k2\Omega\)

=>\(x=-\dfrac{\Omega}{4}+k\Omega\)

a: \(1+tan^2x=1+\left(\dfrac{sinx}{cosx}\right)^2\)

\(=1+\dfrac{sin^2x}{cos^2x}=\dfrac{cos^2x+sin^2x}{cos^2x}=\dfrac{1}{cos^2x}\)

b: \(tanx+cotx=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}\)

\(=\dfrac{sin^2x+cos^2x}{sinx\cdot cosx}=\dfrac{1}{sinx\cdot cosx}\)

Đáp án C

Phương trình tương đương với:

Phương trình có nghiệm:

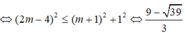
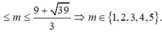
Có 5 số nguyên thoả mãn

\(2sin2x+sinx.cosx-cos^2x+1=0\)

\(\Leftrightarrow4sin2x+2sinx.cosx-2cos^2x+2=0\)

\(\Leftrightarrow4sin2x+sin2x-cos2x=-1\)

\(\Leftrightarrow5sin2x-cos2x=-1\)

\(\Leftrightarrow\sqrt{26}\left(\dfrac{5}{\sqrt{26}}sin2x-\dfrac{1}{\sqrt{26}}cos2x\right)=-1\)

\(\Leftrightarrow cos\left(2x+arccos\dfrac{1}{\sqrt{26}}\right)=\dfrac{1}{\sqrt{26}}\)

\(\Leftrightarrow2x+arccos\dfrac{1}{\sqrt{26}}=\pm arccos\dfrac{1}{\sqrt{26}}+k2\pi\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=-arccos\dfrac{1}{\sqrt{26}}+k\pi\end{matrix}\right.\)