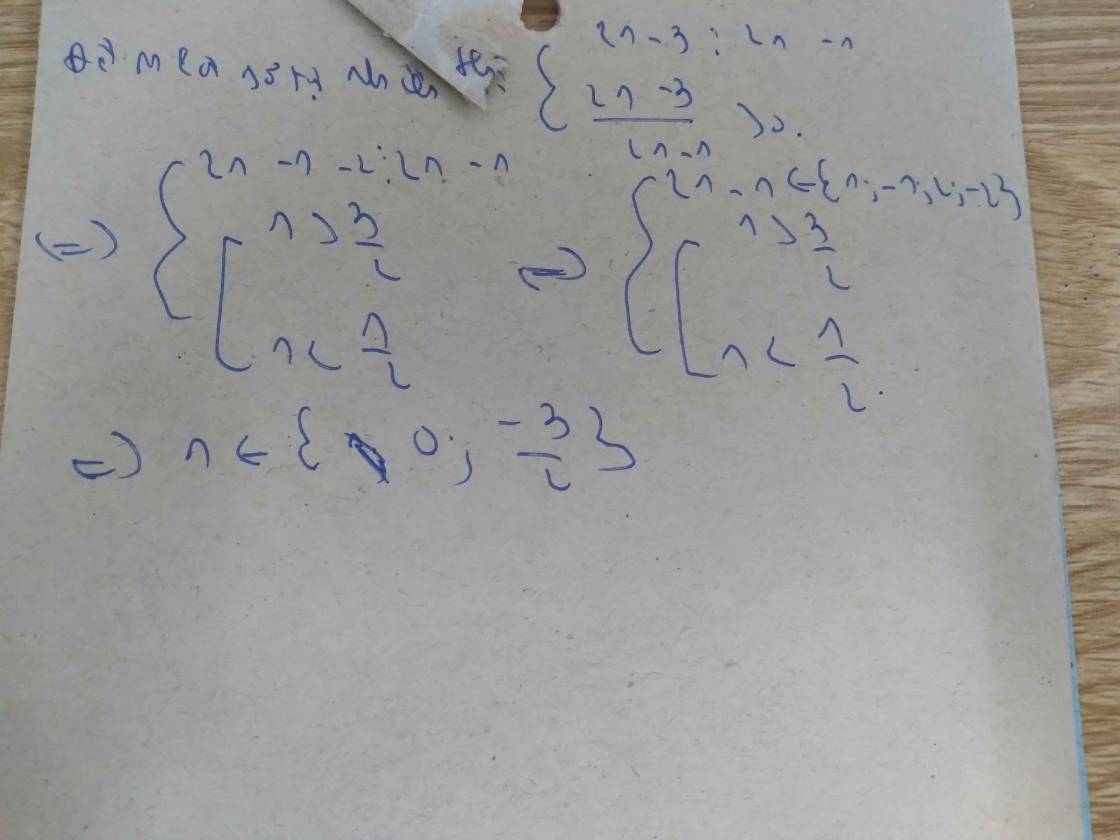M=1 + 3 + 5 . . .+ (2n-1) (Với n ϵ N , n ≠ 0)

Những câu hỏi liên quan
Cho M = 1+ 3 + 5 +.......+ ( 2n - 1 ) với n ϵ N và n ≠ 0
Chứng minh M là số chính phương
Số số hạng là (2n-1-1):2+1=n(số)
Tổng là (2n-1+1)*n/2=n^2 là số chính phương
Đúng 1
Bình luận (0)
Bài 1: Tìm n ϵ Z, biết :
a, n + 1 ϵ Ư ( n2 + 2n - 3 )
b, n2 + 2 ϵ B ( n2 + 1 )
c, 2n + 3 ϵ B ( n + 1 )
a) \(n+1\inƯ\left(n^2+2n-3\right)\)
\(\Leftrightarrow n^2+2n-3⋮n+1\)
\(\Leftrightarrow n\left(n+1\right)+n-3⋮n+1\)
Vì \(n\left(n+1\right)⋮n+1\Rightarrow n-3⋮n+1\)
\(\Leftrightarrow n+1-4⋮n+1\)
Vì \(n+1⋮n+1\Rightarrow-4⋮n+1\Rightarrow n+1\inƯ\left(-4\right)=\left\{-1;1;-2;2;-4;4\right\}\)
Ta có bảng sau:
| \(n+1\) | \(-1\) | \(1\) | \(-2\) | \(2\) | \(-4\) | \(4\) |
| \(n\) | \(-2\) | \(0\) | \(-3\) | \(1\) | \(-5\) | \(3\) |
Vậy...
b) \(n^2+2\in B\left(n^2+1\right)\)
\(\Leftrightarrow n^2+2⋮n^2+1\)
\(\Leftrightarrow n^2+1+1⋮n^2+1\)
Vì \(n^2+1⋮n^2+1\) nên \(1⋮n^2+1\Rightarrow n^2+1\inƯ\left(1\right)=\left\{-1;1\right\}\)
Ta có bảng sau:
| \(n^2+1\) | \(-1\) | \(1\) |
| \(n\) | \(\sqrt{-2}\) (vô lý, vì 1 số ko âm mới có căn bậc hai) |
\(0\) (tm) |
Vậy \(n=0\)
c) \(2n+3\in B\left(n+1\right)\)
\(\Leftrightarrow2n+3⋮n+1\)
\(\Leftrightarrow2n+2+1⋮n+1\)
\(\Leftrightarrow2\left(n+1\right)+1⋮n+1\)
Vì \(2\left(n+1\right)⋮n+1\) nên \(1⋮n+1\Rightarrow n+1\inƯ\left(1\right)=\left\{-1;1\right\}\)
Ta có bảng sau:
| \(n+1\) | \(-1\) | \(1\) |
| \(n\) | \(-2\) | \(0\) |
Vậy...
Đúng 0
Bình luận (0)
a) n+1∈Ư(n2+2n−3)n+1∈Ư(n2+2n−3)
⇔n2+2n−3⋮n+1⇔n2+2n−3⋮n+1
⇔n(n+1)+n−3⋮n+1⇔n(n+1)+n−3⋮n+1
Vì n(n+1)⋮n+1⇒n−3⋮n+1n(n+1)⋮n+1⇒n−3⋮n+1
⇔n+1−4⋮n+1⇔n+1−4⋮n+1
Vì n+1⋮n+1⇒−4⋮n+1⇒n+1∈Ư(−4)={−1;1;−2;2;−4;4}n+1⋮n+1⇒−4⋮n+1⇒n+1∈Ư(−4)={−1;1;−2;2;−4;4}
Ta có bảng sau:
| n+1n+1 | −1−1 | 11 | −2−2 | 22 | −4−4 | 44 |
| nn | −2−2 | 00 | −3−3 | 11 | −5−5 | 33 |
Vậy...
b) n2+2∈B(n2+1)n2+2∈B(n2+1)
⇔n2+2⋮n2+1⇔n2+2⋮n2+1
⇔n2+1+1⋮n2+1⇔n2+1+1⋮n2+1
Vì n2+1⋮n2+1n2+1⋮n2+1 nên 1⋮n2+1⇒n2+1∈Ư(1)={−1;1}1⋮n2+1⇒n2+1∈Ư(1)={−1;1}
Ta có bảng sau:
| n2+1n2+1 | −1−1 | 11 |
| nn | √−2−2 (vô lý, vì 1 số ko âm mới có căn bậc hai) |
00 (tm) |
Vậy n=0n=0
c) 2n+3∈B(n+1)2n+3∈B(n+1)
⇔2n+3⋮n+1⇔2n+3⋮n+1
⇔2n+2+1⋮n+1⇔2n+2+1⋮n+1
⇔2(n+1)+1⋮n+1⇔2(n+1)+1⋮n+1
Vì 2(n+1)⋮n+12(n+1)⋮n+1 nên 1⋮n+1⇒n+1∈Ư(1)={−1;1}1⋮n+1⇒n+1∈Ư(1)={−1;1}
Ta có bảng sau:
| n+1n+1 | −1−1 | 11 |
| nn | −2−2 | 00 |
Đúng 0
Bình luận (0)
gọi S là tổng các số nguyên n để 2n + 3/4n + 1 là phân số tối giản :
A, n ≠ 5k + 1 với k ϵ N B, n = 5k + 1 với k ϵ N
C , n ≠ 5k - 1 với k ϵ N C, n = 5k - 1 với k ϵ N
1. Tìm n ϵ Z, biết :
a, n2 - 2n + 3 ⋮ n + 4
b, 3n2 + n + 16 ⋮ n + 5n
c, n3 + n - 5n - 2 ⋮ n + 3
d, n + 4 ⋮ 3 - n
e, 2n + 1 ⋮ 5 - n
Giúp mình với thứ 7 mình phải nộp rồi ạ !
Viết lời giải ra giúp mình nhé !
Đúng 0
Bình luận (0)
tìm n ϵ N* biết 1+3+5+...+(2n-1)
Xem thêm câu trả lời
tìm các giá trị của n để phân số M=\(\dfrac{2n-3}{2n-1}\) (n ϵ N ) là một số tự nhiên
giúp em với ạ, em cần gấp!
(-24). 17. (-3)0. (-5)6.(-12n) ( n ϵ N)
Mong các bạn giải giùm mình nhé
(-24).17.(-3)0.(-5)6.(-12n)
= (-24).17.(-56)
= 4250000
Bài 1: CMR với n ϵ Z các phân số sau tối giản
a) \(\dfrac{n}{2n+1}\)
b) \(\dfrac{n+5}{n+6}\)
c) \(\dfrac{n+1}{2n+3}\)
d) \(\dfrac{3n+2}{5n+3}\)
e)\(\dfrac{1}{7n+1}\)
Các bạn giải chi tiết cho mình nhé. Thanks all !
Cho A = 1 + 3 + 5 + ... + ( 2n - 1 ) ( n ϵ N )
CMR: A là số chính phương
Giải giúp mình với mình đang cần rất gấp!!
Số số hạng của A:
(2n - 1 - 1) : 2 + 1 = (2n - 2) : 2 + 1
= n - 1 + 1
= n
A = (2n - 1 + 1) . n : 2
= 2n . n : 2
= 2n² : 2
= n²
Vậy A là số chính phương (vì n ∈ ℕ)
Đúng 0
Bình luận (0)
A = 1 + 3 + 5 + ... + (2n - 1)
Dãy số trên là dãy số cách đều với khoảng cách là:
3 - 1 = 2
Số số hạng của dãy số trên là:
(2n - 1 - 1) : 2 + 1 = n
A = (2n - 1 + 1).n : 2
A = 2n.n : 2
A = n2
Vậy A là số chính phương ( đpcm vì A là bình phương của một số tự nhiên)
Đúng 0
Bình luận (0)