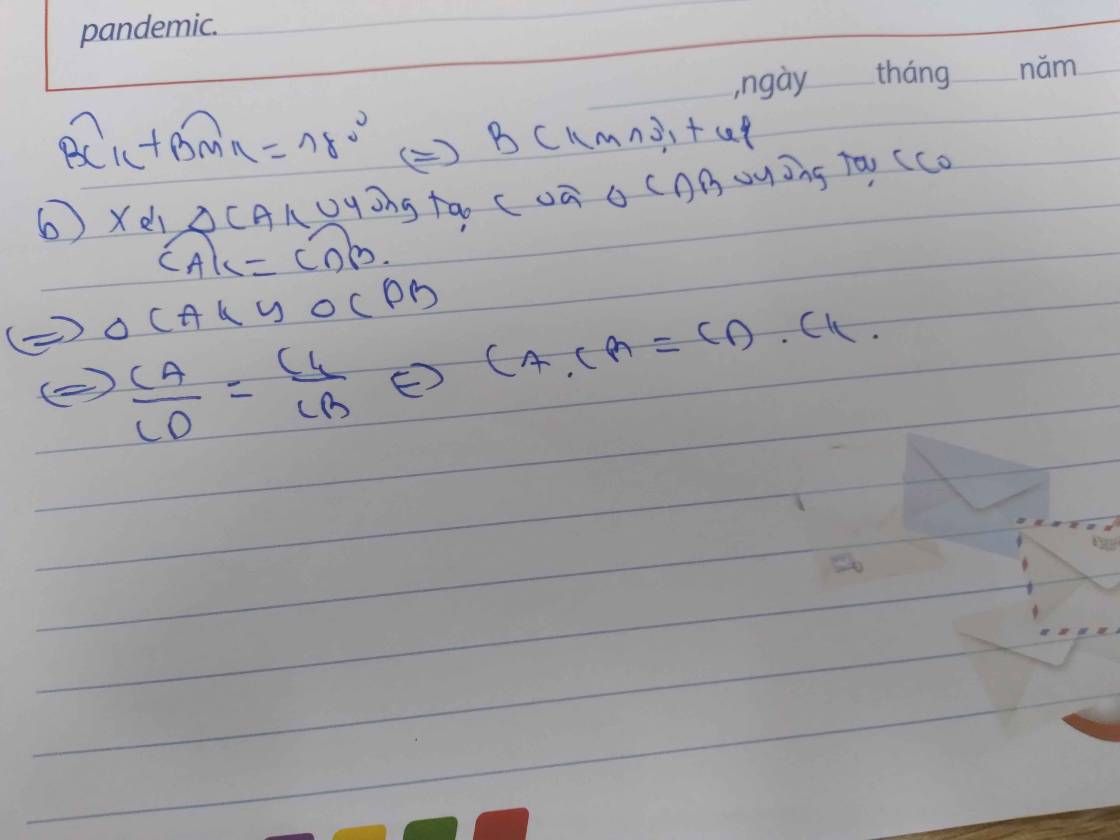Cho nửa (O) đường kính AB=2R,C lad điểm bất kì nằm trên nửa đường tròn sao cho C khác A và AC

Những câu hỏi liên quan
cho nửa (O) đường kính AB2R,C là điểm bất kì nằm trên nửa đường tròn sao cho C khác A va AC CB.Điểm D thuộc cung nhỏ BC sao cho COD90o . Gọi E là giao điểm của AD và BC, F là giao điểm của AC và BD 1.cm:CEDF là tứ giác nội tiếp2.cm:FC.FAFD.FB3.gọi I là trung điểm của EF ,chứng minh IC là tiếp tuyến của (O)4.hỏi C thay đổi thỏa mãn điều kiện bài toán,E thuộc đường tròn cố định nàogiúp mk với nha
Đọc tiếp
cho nửa (O) đường kính AB=2R,C là điểm bất kì nằm trên nửa đường tròn sao cho C khác A va AC< CB.Điểm D thuộc cung nhỏ BC sao cho COD=90o . Gọi E là giao điểm của AD và BC, F là giao điểm của AC và BD
1.cm:CEDF là tứ giác nội tiếp
2.cm:FC.FA=FD.FB
3.gọi I là trung điểm của EF ,chứng minh IC là tiếp tuyến của (O)
4.hỏi C thay đổi thỏa mãn điều kiện bài toán,E thuộc đường tròn cố định nào
giúp mk với nha![]()
Cho nửa đường tròn tâm O, đường kính AB = 2R. Trên nửa đường tròn lấy điểm C bất kì (C khác A và B). Tiếp tuyến tại C và tiếp tuyến tại A cắt nhau tại M. a) Chứng minh bốn điểm, O, A, M, C cùng thuộc một đường tròn. b) AC cắt OM tại H, chứng minh AC vuông góc với OM và 2.OH OM =R mũ 2.
a: Xét tứ giác OAMC có
\(\widehat{OAM}+\widehat{OCM}=180^0\)
Do đó: OAMC là tứ giác nội tiếp
Đúng 0
Bình luận (0)
cho nửa đường tròn tâm O đường kính AB và một điểm C nằm giữa A và B ( AC < AB). Lấy điểm M bất kì trên nửa đường tròn ( M khác A và B). Trên cùng một nửa mặt phẳng bờ AB có chứa M, vẽ các tiếp tuyến Ax, By với nửa đường tròn. Đường thẳng qua M vuông góc với MC cắt tia Ax tại P
Cho nữa đường tròn (O) đường kính AB 2R và điểm C nằm trên nữa đường tròn đó. Kẻ CH vuông góc với AB (H khác O). gọi D là điểm bất kì nằm trên đoạn CD, đường thẳng AD cắt nửa đường tròn tại điểm thứ hai là Ea, CM tứ giácBHDE nội tiếpb, CM AD.ECCD.ACc, khi điểm C di động trên nửa đường tròn (C khác A, B và điểm chính giữa cung AB) , xác định vị trí của điểm C sao cho chu vi △COH đạt gía trị lớn nhất
Đọc tiếp
Cho nữa đường tròn (O) đường kính AB = 2R và điểm C nằm trên nữa đường tròn đó. Kẻ CH vuông góc với AB (H khác O). gọi D là điểm bất kì nằm trên đoạn CD, đường thẳng AD cắt nửa đường tròn tại điểm thứ hai là E
a, CM tứ giácBHDE nội tiếp
b, CM AD.EC=CD.AC
c, khi điểm C di động trên nửa đường tròn (C khác A, B và điểm chính giữa cung AB) , xác định vị trí của điểm C sao cho chu vi △COH đạt gía trị lớn nhất
a: góc AEB=1/2*sđ cung AB=90 độ
Vì góc DHB+góc DEB=180 độ
nên DHBE nội tiếp
b: Xét ΔADC và ΔACE co
góc ACH=góc AEC(=góc ABC)
góc DAC chung
=>ΔADC đồng dạng với ΔACE
=>DC/EC=AD/AC
=>DC*AC=EC*AD
Đúng 1
Bình luận (0)
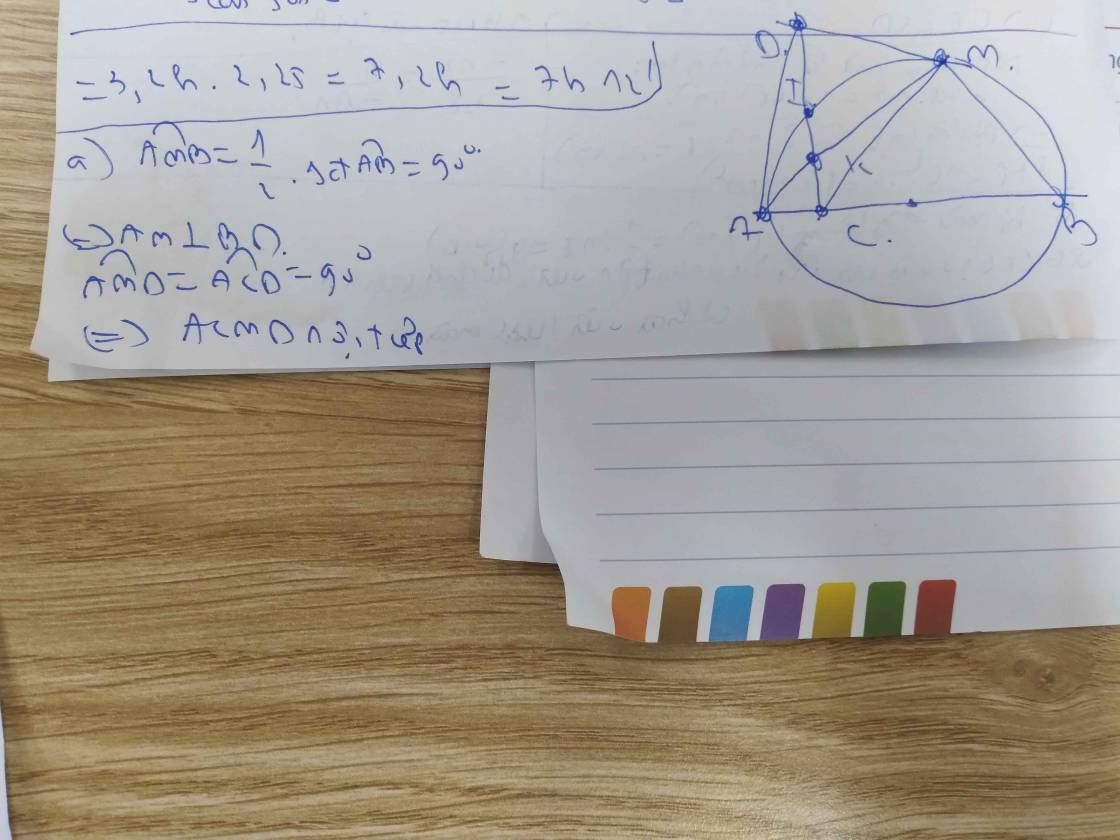
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh :a) Các tứ giác : ACMD ; BCKM nội tiếp đường trònb) CK.CD CA.CBc) Gọi N là giao điểm của AD và (O). Chứng minh rằng : B, K, M thẳng hàng
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh :
a) Các tứ giác : ACMD ; BCKM nội tiếp đường tròn
b) CK.CD = CA.CB
c) Gọi N là giao điểm của AD và (O). Chứng minh rằng : B, K, M thẳng hàng
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A .Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I ,K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I) tia AK cắt nửa đường tròn O tại M tia BM cắt tia CI tại D .Chứng minh : a)Các tứ giác ACMD,BCKM nội tiếp đường tròn b)CK.CDCA.CB c) Gọi N là giao điểm của AD và đường tròn O chứng minh B,K,N thẳng hàng
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A .Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I ,K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I) tia AK cắt nửa đường tròn O tại M tia BM cắt tia CI tại D .Chứng minh : a)Các tứ giác ACMD,BCKM nội tiếp đường tròn b)CK.CD=CA.CB c) Gọi N là giao điểm của AD và đường tròn O chứng minh B,K,N thẳng hàng
Trên nửa đường tròn tâm O đường kính AB 2R, lấy điểm C (C khác A, B), từ C kẻ CH vuông góc AB (H thuộc AB). Gọi D là điểm bất kì trên đoạn CH (D khác C và H), đường thẳng AD cắt nửa đường tròn tại điểm thứ hai là E.a. CM tứ giác BHDE nội tiếp.b. CM AD.EC CD.ACc. Khi điểm C di động trên nửa đường tròn (C khác A, B và điểm chính giữa cung AB), xác định vị trí của điểm C sao cho chu vi tam giác COH đạt GTLN.Dạ bày em câu (c) với ạ, giải chi tiết giúp em:)
Đọc tiếp
Trên nửa đường tròn tâm O đường kính AB = 2R, lấy điểm C (C khác A, B), từ C kẻ CH vuông góc AB (H thuộc AB). Gọi D là điểm bất kì trên đoạn CH (D khác C và H), đường thẳng AD cắt nửa đường tròn tại điểm thứ hai là E.
a. CM tứ giác BHDE nội tiếp.
b. CM AD.EC = CD.AC
c. Khi điểm C di động trên nửa đường tròn (C khác A, B và điểm chính giữa cung AB), xác định vị trí của điểm C sao cho chu vi tam giác COH đạt GTLN.
Dạ bày em câu (c) với ạ, giải chi tiết giúp em:")
Đặt chu vi COH là \(P=OC+OH+CH\)
Ta có:
\(P=OC+OH+CH\le OC+\sqrt{2\left(OH^2+CH^2\right)}=OC+\sqrt{2OC^2}=OC\left(1+\sqrt{2}\right)=R\left(1+\sqrt{2}\right)\)
Dấu "=" xảy ra khi \(OH=CH\Rightarrow\Delta OCH\) vuông cân tại H
\(\Rightarrow\widehat{COH}=45^0\) hay C là điểm nằm trên cung AB sao cho OC hợp với AB 1 góc 45 độ
//Phía trên sử dụng BĐT \(a+b\le\sqrt{2\left(a^2+b^2\right)}\) để đánh giá
Đúng 5
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB = 2R. Vẽ tia tiếp tuyến Ax. Từ điểm M trên Ax kẻ MC (C nằm trên nữa đường tròn và khác A) sao cho MA bằng MC. Nối M với O; MB cắt nửa đường tròn (O) tại D.
a. Chứng minh: AMCO là tứ giác nội tiếp đường tròn. Xác định tâm I của đường tròn.
b. Chứng minh: MC là tiếp tuyến; MC2 = MD.MB.
a: Xét ΔMAO và ΔMCO có
MA=MC
AO=CO
MO chung
=>ΔMAO=ΔMCO
=>góc MCO=90 độ
góc MAO+góc MCO=180 độ
=>MAOC nội tiếp đường tròn đường kính MO
=>I là trung điểm của MO
b: góc MCO=90 độ
=>MC là tiếp tuyến của (O)
Xét ΔMCD và ΔMBC có
góc MCD=góc MBC
góc CMD chung
=>ΔMCD đồng dạng với ΔMBC
=>MC/MB=MD/MC
=>MC^2=MB*MD
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB = 2R. C là trung điểm của đoạn OA, đường thẳng Cx vuông góc với AB, Cx cắt nửa đường tròn ( O ) tại I. K là 1 điểm bất kì nằm trên đoạn CI ( K khác C, K khác I ), tia AK cắt nửa đường tròn tại M.
Tính diện tích tam giác ABD khi K là trung điểm của đoạn thẳng CI?
Ơ , em tưởng chị " ko cần bít " cơ mà ?
Đúng 0
Bình luận (0)