Cho tgiac ABC có góc A =1200 . O là giao điểm của 3 đường phân giác trong tgiac ABC . Tính góc BOC . Cho hình vẻ với

Những câu hỏi liên quan
cho tam giác ABC, có BAC=90 độ, đường phân giác trong của góc A cắt BC tại D. Từ D kẻ DE vuông góc với AB, DF vuông gíc với AC.
a) CM tam giác ADE= tgiac ADF
b) CM rằng tgiac DEF là tgiac đều
c) Qua điểm C vẽ đường thẳng song song với AD, nó cắt đường thẳng AB tại M. CM tgiac ACM là tgiac đều
cho tam giác abc vuông tại a. tia phân giác của góc abc cắt cạnh ac tại e, từ e kẻ em vuông góc với bc tại m
1) CM: tgiac BEA = tgiac BEM
2) CM: BE vuông góc với AM
3) gọi n là giao điểm của tia ME với tia BA. CM: tgiac AEN = tgiac MEC
4) CM: AM // NC
MN GIÚP MIK NHÉ, MIK ĐAG CẦN GẤP LẮM
1/ Xét tg vuông BEA và tg vuông BEM có
BE chung; \(\widehat{ABE}=\widehat{MBE}\Rightarrow\Delta BEA=\Delta BEM\) (Hai tg vuông có cạnh huyền và 1 góc nhọn bằng nhau)
2/
\(\Delta BEA=\Delta BEM\Rightarrow BA=BM\) => tg BAM cân tại B \(\Rightarrow BE\perp AM\) (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao)
3/ Xét tg vuông AEN và tg vuông MEC có
\(\Delta BEA=\Delta BEM\Rightarrow AE=ME\)
\(\widehat{AEN}=\widehat{MEC}\) (góc đối đỉnh)
\(\Rightarrow\Delta AEN=\Delta MEC\) (hai tg vuông có cạnh góc vuông và góc nhọn tương ứng bằng nhau) \(\Rightarrow AN=MC\)
4/ Ta có
BA=BM; AN=MC (cmt) => BA+AN=BM+MC => BN=BC => tg BNC cân tại B
Mà \(\widehat{ABE}=\widehat{MBE}\)
\(\Rightarrow BE\perp NC\) (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao)
Ta có \(BE\perp AM\left(cmt\right)\)
=> AM // NC (cùng vuông góc với BE)
Cho tam giác ABC nhọn có 3 đường cao AD,BE,CF cắt nhau tại H.Từ B kẻ tia Bx vuông góc với BA, từ C kẻ tia Cy vuông góc với CA. Gọi giao của Bx và Cy là K
1 tứ giác BHCK là hình gì? Tại sao?
2 chứng minh tgiac HAB đồng dạng vs tgiac HED
cho tam giác ABC vuông tại A (AB<AC), đường cao AH a, CM tgiac ABC đồng dạng với tgiac HBA từ đó suy ra AB.AB=BC.BH, AB.AC=BC.AH b, CM tgiac ABC đồng dạng với tgiac HAC từ đó suy ra AC.AC=BC.CH c, tia phân giác của góc ABC cắt AH tại K, cắt AC tại I. CM: tgiac ABK đồng dạng tgiac CBI d, CM AI/IC=KH/AK
Cho tam giác ABC vuông tại A có C = 30°. Kẻ AH vuông góc với BC ( H€ BC) và tia phân giác AD của góc HAC (D€BC)
a. Tính số đo góc B, góc DAC
b. Trên cạnh AC lấy điểm E sao cho AE =AH. Cm tgiac ADH.= tgiac ADE và DE vuông góc với AC
c. Trên tia đối của tia HA lấy điểm F sao cho HF = EC. Cm F,D,E thẳng hàng.
Giúp mk nha các bạn.
Xem chi tiết
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{ABC}=90^0-\widehat{ACB}=90^0-30^0\)
hay \(\widehat{ABC}=60^0\)
Ta có: ΔAHB vuông tại A(AH⊥BC)
nên \(\widehat{BAH}+\widehat{ABH}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{BAH}=90^0-\widehat{ABH}=90^0-60^0=30^0\)
Ta có: tia AH nằm giữa hai tia AB,AC
nên \(\widehat{BAH}+\widehat{CAH}=\widehat{BAC}\)
hay \(30^0+\widehat{CAH}=90^0\)
\(\Leftrightarrow\widehat{CAH}=60^0\)
Ta có: AD là tia phân giác của \(\widehat{CAH}\)(gt)
nên \(\widehat{DAC}=\dfrac{\widehat{CAH}}{2}=\dfrac{60^0}{2}=30^0\)
Vậy: \(\widehat{ABC}=60^0\); \(\widehat{DAC}=30^0\)
b) Xét ΔADH và ΔADE có
AH=AE(gt)
\(\widehat{HAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{HAE}\))
AD chung
Do đó: ΔADH=ΔADE(c-g-c)
⇒\(\widehat{AHD}=\widehat{AED}\)(hai góc tương ứng)
mà \(\widehat{AHD}=90^0\)(AH⊥HD)
nên \(\widehat{AED}=90^0\)
hay DE⊥AC(đpcm)
c) Ta có: ΔAHD=ΔAED(cmt)
nên HD=ED(hai cạnh tương ứng)
Xét ΔFHD vuông tại H và ΔCED vuông tại E có
FH=CE(gt)
HD=ED(cmt)
Do đó: ΔFHD=ΔCED(cạnh huyền-cạnh góc vuông)
⇒\(\widehat{FDH}=\widehat{CDE}\)(hai góc tương ứng)
mà \(\widehat{CDE}+\widehat{HDE}=180^0\)(hai góc kề bù)
nên \(\widehat{FDH}+\widehat{EDH}=180^0\)
⇒\(\widehat{FDE}=180^0\)
hay F,D,E thẳng hàng(đpcm)
Đúng 2
Bình luận (0)
Cho tgiac ABC vuông tại A(ABAC), vẽ đường cao AH. Trên đoạn thẳng HC lấy điểm M (M ko trùng với H và C), từ M vẽ MN vuông góc với AC tại N.a. CMinh tgiac CMM đồng dạng với tam giác CAH và CA.CNCH.CMb. CMinh tgiac AMC đồng dạng với tgiac HNCc. Trên tia đối tia AC lấy điểm D sao cho ADAC. Vẽ AE vuông góc với BD tại E . Cminh rằng góc BEHgóc BCNd. Gọi K,F lần lượt là trung điểm của BH và BD.I là giao điểm của EK và CF. CMinh rằng KC.IEEF.IC
Đọc tiếp
Cho tgiac ABC vuông tại A(AB<AC), vẽ đường cao AH. Trên đoạn thẳng HC lấy điểm M (M ko trùng với H và C), từ M vẽ MN vuông góc với AC tại N.
a. CMinh tgiac CMM đồng dạng với tam giác CAH và CA.CN=CH.CM
b. CMinh tgiac AMC đồng dạng với tgiac HNC
c. Trên tia đối tia AC lấy điểm D sao cho AD<AC. Vẽ AE vuông góc với BD tại E . Cminh rằng góc BEH=góc BCN
d. Gọi K,F lần lượt là trung điểm của BH và BD.I là giao điểm của EK và CF. CMinh rằng KC.IE=EF.IC
Cho tgiac ABC vuông tại A có AB=12cm,AC=16cm, có phân giác BD(D thuộc AC) a) TÍnh DA,DC b) Kẻ đường cao AH của tam giác ABC. CMinh tgiac AHB đồng dạng vs tam giác ABC c) C/minh:AH.AH=HB.HC d) Kẻ DK vuông góc BC tại K. Tính HK
Cho tgiac ABC vuông tại A. Trên cạnh BC lấy E sao cho AB BE. Tia phân giác của B cắt cạnh AC ở Da) chứng minh tgiac ABD tgiac EBDb) chứng minh: BD vuông góc với AE tại trung điểm I của đoạn AEc) kẻ AH vuông góc với BC, (H thuộc BC) chứng minh AH // DEd) so sánh ABC EDCe) gọi K là giao điểm của ED và BA, M là trung điểm KC. chứng minh B, D, M thẳng hàng - Ghi GT - KL với vẽ hình đầy đủ giúp tớ với nhaa
Đọc tiếp
Cho tgiac ABC vuông tại A. Trên cạnh BC lấy E sao cho AB = BE. Tia phân giác của B cắt cạnh AC ở D
a) chứng minh tgiac ABD = tgiac EBD
b) chứng minh: BD vuông góc với AE tại trung điểm I của đoạn AE
c) kẻ AH vuông góc với BC, (H thuộc BC) chứng minh AH // DE
d) so sánh ABC = EDC
e) gọi K là giao điểm của ED và BA, M là trung điểm KC. chứng minh B, D, M thẳng hàng
- Ghi GT - KL với vẽ hình đầy đủ giúp tớ với nhaa
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>BA=BE
=>B nằm trên đường trung trực của AE(2)
Ta có: ΔBAD=ΔBED
=>DA=DE
=>D nằm trên đường trung trực của AE(1)
Từ (1) và (2) suy ra BD là đường trung trực của AE
=>BD\(\perp\)AE tại trung điểm I của AE
c: Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
Ta có: AH\(\perp\)BC
DE\(\perp\)BC
Do đó: AH//DE
d: Ta có: \(\widehat{EDC}+\widehat{ACB}=90^0\)(ΔEDC vuông tại E)
\(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{EDC}=\widehat{ABC}\)
e: Xét ΔDAK vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAK=ΔDEC
=>DK=DC và AK=EC
Ta có: BK=BA+AK
BC=BE+EC
mà BA=BE và AK=EC
nên BK=BC
=>B nằm trên đường trung trực của KC(3)
Ta có: DK=DC
=>D nằm trên đường trung trực của KC(4)
Ta có: MK=MC
=>M nằm trên đường trung trực của CK(5)
Từ (3),(4),(5) suy ra B,D,M thẳng hàng
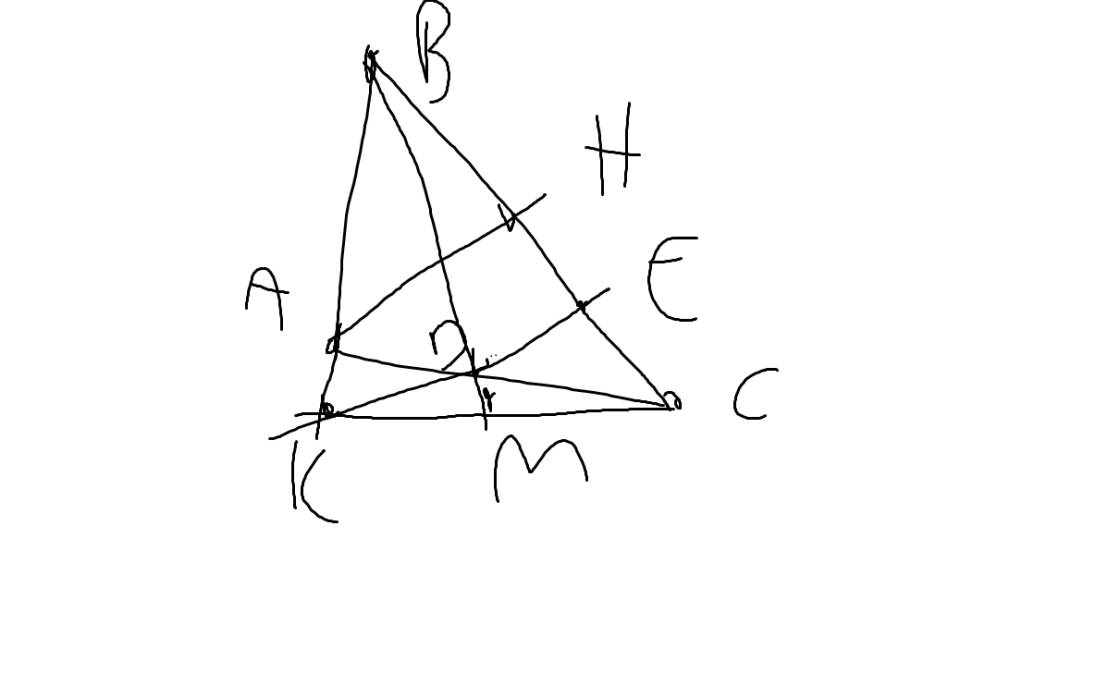
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A ( AB AC ) trên nửa mặt phẳng bờ AB có chứa điểm C vez tia Bx vuông góc với AB trên tia Bx lấy điểm D sao BD AC a, chúng minh tgiac ABC tgiac BADb, gọi E là giao điểm của AD và BC . chứng minh AD//BD và EA ED c, gọi m là trung điểm thuộc đoạn thẳng bd qua d vẽ dường thẳng song song với ma đường thẳng này cắt đoạn thẳng ac tại n chứng minh dn ma d, chứng minh e là trung điểm của nm
Đọc tiếp
cho tam giác ABC vuông tại A ( AB < AC ) trên nửa mặt phẳng bờ AB có chứa điểm C vez tia Bx vuông góc với AB trên tia Bx lấy điểm D sao BD = AC
a, chúng minh tgiac ABC = tgiac BAD
b, gọi E là giao điểm của AD và BC . chứng minh AD//BD và EA = ED
c, gọi m là trung điểm thuộc đoạn thẳng bd qua d vẽ dường thẳng song song với ma đường thẳng này cắt đoạn thẳng ac tại n chứng minh dn = ma
d, chứng minh e là trung điểm của nm
a: Xet ΔABC vuông tại A và ΔBAD vuông tại B có
AB chung
AC=BD
Do đó: ΔABC=ΔBAD
b: Xét tứ giác ABDC có
AC//BD
AC=BD
Do đó; ABDC là hình bình hành
=>AD cắt BC tại trung điểm của mỗi đường
=>EA=ED
c: Xét tứ giác AMDN có
AM//DN
AN//MD
Do đó:AMDN là hình bình hành
=>DN=MA
Đúng 0
Bình luận (0)













