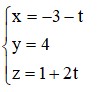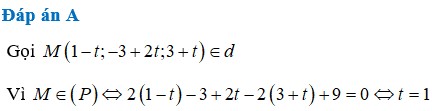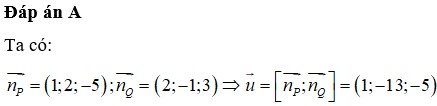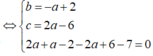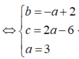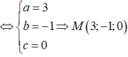Tìm giao điểm của đường thẳng d (x-1)/2=y+1/-1=z/3 và mặt phẳng 2x-y+3z-4=0

Những câu hỏi liên quan
Trong không gian Oxyz cho đường thẳng d:
x
-
1
2
y
-
2
-
1
z
-
3
1
và mặt phẳng (P): 2x +y +z+ 1 0. Phương trình đường thẳng qua giao điểm của đường thẳng (d) với (P), nằm trên mặt phẳng...
Đọc tiếp
Trong không gian Oxyz cho đường thẳng
d: x - 1 2 = y - 2 - 1 = z - 3 1 và mặt phẳng
(P): 2x +y +z+ 1 = 0. Phương trình đường
thẳng qua giao điểm của đường thẳng (d)
với (P), nằm trên mặt phẳng (P) và vuông
góc với đường thẳng d là.
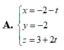
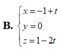
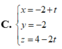
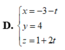
Trong không gian Oxyz cho đường thẳng
(
d
)
:
x
-
1
2
y
-
2
-
1
z
-
3
1
và mặt phẳng
(
P
)
:
2...
Đọc tiếp
Trong không gian Oxyz cho đường thẳng ( d ) : x - 1 2 = y - 2 - 1 = z - 3 1 và mặt phẳng ( P ) : 2 x + y + z = 0 . Phương trình đường thẳng qua giao điểm của đường thẳng (d) với (P), nằm trên mặt phẳng (P) và vuông góc với đường thẳng d là.
A. x = - 2 - t y = - 2 z = 3 + 2 t
B. x = - 1 + t y = 0 z = 1 - 2 t
C. x = - 2 + t y = - 2 z = 4 - 2 t
D. x = - 3 - t y = 4 z = 1 + 2 t
Cho đường thẳng
d
x
1
-
2
t
y
2
+
t
z
3
-...
Đọc tiếp
Cho đường thẳng d x = 1 - 2 t y = 2 + t z = 3 - t và mặt phẳng P : 2 x + y + z = 0 . Tìm tọa độ giao điểm A của d và (P)
A. A 15 4 ; - 10 4 ; 5 4
B. A - 2 ; 1 ; 1
C. A - 10 4 ; 15 4 ; 5 4
D. A 1 ; 2 ; - 4
Trong không gian Oxyz, cho đường thẳng
d
:
x
-
1
-
1
y
+
3
2
z
-
3
1
và cho mặt phẳng (P): 2x+y-2z+90....
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng d : x - 1 - 1 = y + 3 2 = z - 3 1 và cho mặt phẳng (P): 2x+y-2z+9=0. Tìm tọa độ giao điểm của d và (P)
A. (0;-1;4)
B. (0;1;4)
C. (0;-1;-4)
D. (0;1;-4)
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) và đường thẳng d tương ứng có phương trình là
2
x
-
y
+
3
z
-
3
0
và
x
+
1
-
2
y
-
2
1
z...
Đọc tiếp
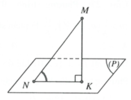
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) và đường thẳng d tương ứng có phương trình là 2 x - y + 3 z - 3 = 0 và x + 1 - 2 = y - 2 1 = z + 2 - 1 . Biết đường thẳng d cắt mặt phẳng (P) tại điểm M. Gọi N là điểm thuộc d sao cho M N = 3 , gọi K là hình chiếu vuông góc của điểm N trên mặt phẳng (P). Tính độ dài đoạn MK.
A. M K = 7 105
B. M K = 7 4 21
C. M K = 4 21 7
D. M K = 105 7
Gọi d là đường thẳng giao tuyến của hai mặt phẳng (P): x+2y-5z+10 và (Q): 2x-y+3z-10. Tính véc tơ chỉ phương
u
→
của d A.
u
→
(
1
;
-
13
;
-
5
)
B.
u
→
(
1
;
13
;
-
5
)...
Đọc tiếp
Gọi d là đường thẳng giao tuyến của hai mặt phẳng (P): x+2y-5z+1=0 và (Q): 2x-y+3z-1=0. Tính véc tơ chỉ phương u → của d
A. u → = ( 1 ; - 13 ; - 5 )
B. u → = ( 1 ; 13 ; - 5 )
C. u → = ( 1 ; - 13 ; 5 )
D. u → = ( 1 ; 13 ; 5 )
Trong không gian Oxyz, giao điểm của đường thẳng
d
:
x
-
3
1
y
+
1
-
1
z
2
và mặt phẳng (P): 2x-y-z-70 có tọa độ là:
Đọc tiếp
Trong không gian Oxyz, giao điểm của đường thẳng d : x - 3 1 = y + 1 - 1 = z 2 và mặt phẳng (P): 2x-y-z-7=0 có tọa độ là:
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng
∆
:
x
-
1
2
y
-
1
1
z
-
1
-
1
và mặt phẳng
P
: x+y+z-30. Gọi d là đường thẳng nằm trong...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng ∆ : x - 1 2 = y - 1 1 = z - 1 - 1 và mặt phẳng P : x+y+z-3=0. Gọi d là đường thẳng nằm trong (P), đi qua giao điểm của Δ và (P), đồng thời vuông góc với Δ. Giao điểm của đường thẳng d với mặt phẳng tọa độ (Oxy) là
A. M(2;2;0)
B. M(-3;2;0)
C. M(-1;4;0)
D. M(-3;4;0)
Cho mặt phẳng (
α
) : 2x + y + z – 1 0 và đường thẳng d:
x
-
1
2
y
1
z
+
1
-
3
Gọi M là...
Đọc tiếp
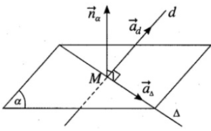
Cho mặt phẳng ( α ) : 2x + y + z – 1 = 0 và đường thẳng d: x - 1 2 = y 1 = z + 1 - 3
Gọi M là giao điểm của d và ( α ), hãy viết phương trình của đường thẳng ∆ đi qua M vuông góc với d và nằm trong ( α )
Xét phương trình:
2(1 + 2t) + (t) + (−2 – 3t) – 1 = 0 ⇔ 2t – 1= 0 ⇔ t = 1/2
Vậy đường thẳng d cắt mặt phẳng ( α ) tại điểm M(2; 1/2; −7/2).
Ta có vecto pháp tuyến của mặt phẳng ( α ) và vecto chỉ phương của đường thẳng d lần lượt là n α → = (2; 1; 1) và a d → = (2; 1; −3).
Gọi a ∆ → là vecto pháp tuyến của Δ, ta có a ∆ → ⊥ n α → và a ∆ → ⊥ a d →
Suy ra a ∆ → = n α → ∧ n d → = (−4; 8; 0) hay a ∆ → = (1; −2; 0)
Vậy phương trình tham số của
∆
là 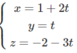
Đúng 0
Bình luận (0)