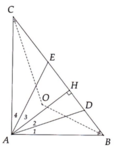
Cho tam giác ABC vuông ở A kẻ AH\(⊥\)BC , H thuộc BC. Tia phân giác của \(\widehat{HAB}\)cắt BC tại D, tia phân giác của \(\widehat{HAC}\)cắt BC tại E. CMR Điểm cách đều 3 cạnh của tam giác ABC chính là điểm cách đều 3 đỉnh của tam giác ADE

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC, H thuộc BC. Tia phân giác của góc
H
A
B
^
cắt BC tại D, tia phân giác của góc
H
A
C
^
cắt BC tại E. Chứng minh điểm cách đều ba cạnh của tam giác ABC chính là điểm cách đều ba đỉnh của tam giác ADE.
Đọc tiếp
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC, H thuộc BC. Tia phân giác của góc H A B ^ cắt BC tại D, tia phân giác của góc H A C ^ cắt BC tại E. Chứng minh điểm cách đều ba cạnh của tam giác ABC chính là điểm cách đều ba đỉnh của tam giác ADE.
Cho tam giác ABC vuông tại A. Kẻ Ah vuông góc với BC (H thuộc BC). Tia phân giác của góc HAC cắt BC tại D. Tia phân giác của góc HAB cắt BC tại E. Chứng minh rằng AB + AC = BC + DE
cho tam giác ABC vuông tại A . Kẻ AH vuông góc với BC . tia phân giác của góc HAB cắt BC tại E , tia phân giác của góc HAC cắt BC tại D . CMR AB+AC=BC=DE
mot mieng dat hinh tam giac co day la 15m va chieu cao la 7,8m nay nguoi ta mo rong mieng dat ve ben phai bang cach keo dai canh day them 3,5m hay tinh dien h manh dat sau khi mo rong
cho tam giác ABC vuông tại A, đường cao AH ( AH thuộc BC ). tia phân giác của HAB cắt cạnh BC tại D, tia phân giác của góc HAC cắt cạnh BC tại E. Trên cạnh AC lấy điểm F sao cho AF=AH
a) tính số đo góc DAE
b)chứng minh tam giác AEH= tam giác AEF
c) chứng minh AB//EF
Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC. tia phân giác của góc HAB cắt BC ở D, tia phân giác của HAC cắt BC ở E. Chứng minh rằng: giao điểm các đường phân giác của tam giác ABC là giao điểm các đường trung trực của tam giác ADE.
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC). Tia phân giác của góc HAC cắt BC tại D. Tia phân giác của góc HAB cắt tại E. Chứng minh rằng: AB + AC = DC + DE
Có thể thấy rằng DC + DE = EC < BC mà BC < AB + AC (bất đẳng thức tam giác) nên AB + AC > DC + DE.
Đề sai rồi bạn.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
B1: Cho tam giác ABC có góc C bằng 30 độ. Tia phân giác của góc B và đường phân giác góc ngoài tại A cắt nhau ở E. Tính số đo góc BCEB2: Cho tam giác ABC có I là giao điểm các tia pg của góc B và góc C. Gọi D là giao điểm của AI và BC. Kẻ IH vuông góc BC (H thuộc BC) CMR: góc BIH góc CIDB3: Cho tam giác ABC vuông tại A. Kẻ AH vuông góc BC. (H thuộc BC), các tia pg của góc HAC và AHC cắt nhau ở I. Tia phân giác của góc HAB cắt BC ở D. Cm: CI điq ua trung điểm của AD
Đọc tiếp
B1: Cho tam giác ABC có góc C bằng 30 độ. Tia phân giác của góc B và đường phân giác góc ngoài tại A cắt nhau ở E. Tính số đo góc BCE
B2: Cho tam giác ABC có I là giao điểm các tia pg của góc B và góc C. Gọi D là giao điểm của AI và BC. Kẻ IH vuông góc BC (H thuộc BC) CMR: góc BIH = góc CID
B3: Cho tam giác ABC vuông tại A. Kẻ AH vuông góc BC. (H thuộc BC), các tia pg của góc HAC và AHC cắt nhau ở I. Tia phân giác của góc HAB cắt BC ở D. Cm: CI điq ua trung điểm của AD
1.Cho tam giác ABC có Â = 90 độ. Kẻ AH vuông góc với BC (h thuộc BC). Tia phân giác góc HAC cắt BC tại D. Tia phân giác HAB cắt BC tại E. CMR: AB + AC = BC + DE
cho tam giác ABC vuông tại A, đường cao AH ( AH thuộc BC ). tia phân giác của HAB cắt cạnh BC tại D, tia phân giác của góc HAC cắt cạnh BC tại E. Trên cạnh AC lấy điểm F sao cho AF=AH
a) tính số đo góc DAE
b)chứng minh tam giác AEH= tam giác AEF
c) chứng minh AB//EF
a: \(\widehat{DAE}=\dfrac{1}{2}\left(\widehat{HAB}+\widehat{HAC}\right)=\dfrac{1}{2}\cdot90^0=45^0\)
b: Xét ΔAEH và ΔAEF có
AE chung
\(\widehat{HAE}=\widehat{FAE}\)
AH=AF
Do đó: ΔAEH=ΔAEF
c: Ta có: ΔAEH=ΔAEF
nên \(\widehat{AHE}=\widehat{AFE}=90^0\)
=>EF⊥AC
mà AC⊥AB
nên EF//AB
Đúng 2
Bình luận (1)