Cho 10 điểm trong đó không có bất kì 3 điểm nào thẳng hàng.
a. Tính số tam giác có 3 đỉnh là 3 trong số 10 điểm trên ?
b. Hãy tổng quát bài toán ( với n điểm )
Những câu hỏi liên quan
Cho 15 điểm phân biệt, trong đó có 6 điểm thẳng hàng, trong số 9 điểm còn lại không có 3 điểm nào
thẳng hàng và không có 2 điểm nào thẳng hàng với bất kì 1 điểm nào đó trong 6 điểm nêu ở trên. Hỏi có bao
nhiêu tam giác mà các đỉnh của chúng lấy từ 15 điểm đã cho?
Chọn 3 điểm trong 15 điểm có: \(C^3_{15}\)(cách chọn)
Chọn 3 điểm trong 6 điểm thẳng hàng có:\(C^3_6\)(cách)
=>Số tam giác được tạo thành từ 15 điểm đã cho là: \(C^3_{15}-C^3_6\)(tam giác)
Đúng 1
Bình luận (0)
a) Có 12 điểm trên 1 mặt phẳng trong đó không có 3 điểm nào thẳng hàng. Hai điểm bất kì nào cũng đc nối với nhau bởi 1 đoạn thẳng. Có bao nhiêu tam giác có đỉnh là 3 trong 12 điểm trên
b) Cho góc xAy . Trên tia Ax lấy 6 điểm khác A, trên tia Ay lấy 5 điểm khác A. trong 12điểm nói trên (kể cả điểm A), hai điểm nào cũng đc nối với nhau bởi 1 đoạn thẳng . Có bao nhiêu tam giác mà các đỉnh là 3 trong 12 điểm trên.
Mình cần gấp, nên giải hộ mik 2 ý nhé. Mik cảm ơn trước
Đọc tiếp
a) Có 12 điểm trên 1 mặt phẳng trong đó không có 3 điểm nào thẳng hàng. Hai điểm bất kì nào cũng đc nối với nhau bởi 1 đoạn thẳng. Có bao nhiêu tam giác có đỉnh là 3 trong 12 điểm trên
b) Cho góc xAy . Trên tia Ax lấy 6 điểm khác A, trên tia Ay lấy 5 điểm khác A. trong 12điểm nói trên (kể cả điểm A), hai điểm nào cũng đc nối với nhau bởi 1 đoạn thẳng . Có bao nhiêu tam giác mà các đỉnh là 3 trong 12 điểm trên.
Mình cần gấp, nên giải hộ mik 2 ý nhé. Mik cảm ơn trước
Trong mặt phẳng cho 10 điểm phân biệt
A
1
,
A
2
,
…
,
A
10
trong đó có 4 điểm
A
1
,
A
2
,
A
3
,
A
4
thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Số tam giác có 3 đỉnh được lấy...
Đọc tiếp
Trong mặt phẳng cho 10 điểm phân biệt A 1 , A 2 , … , A 10 trong đó có 4 điểm A 1 , A 2 , A 3 , A 4 thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Số tam giác có 3 đỉnh được lấy trong 10 điểm trên là
A.116 tam giác
B. 80 tam giác
C. 96 tam giác
D. 60 tam giác
Chọn A
Số tam giác được tạo thành từ 10 điểm là C 10 3 tam giác
Do 4 điểm A 1 , A 2 , A 3 , A 4 thẳng hàng nên số tam giác mất đi là C 10 3
Vậy số tam giác thỏa mãn yêu cầu đề bài là C 10 3 - C 4 3 = 116 tam giác
Đúng 0
Bình luận (0)
Trong mặt phẳng cho 10 điểm phân biệt
A
1
,
A
2
,
.
.
.
A
10
trong đó có 4 điểm
A
1
,
A
2
,
A
3
,
A
4
thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Số tam giác có 3 đỉnh...
Đọc tiếp
Trong mặt phẳng cho 10 điểm phân biệt A 1 , A 2 , . . . A 10 trong đó có 4 điểm A 1 , A 2 , A 3 , A 4 thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Số tam giác có 3 đỉnh được lấy trong 10 điểm trên là
Cho 4 điểm A, B, C, D trong đó không có 3 điểm nào thẳng hàng. Tính số tam giác có ba đỉnh là 3 trong 4 điểm trên. Viết tên các tam giác đó.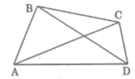
Ta có 4 tam giác: Δ ABC, ΔABD, ΔBCD, ΔACD
Đúng 0
Bình luận (0)
Cho 4 điểm A, B, C, D trong đó không có 3 điểm nào thẳng hàng. Tính số tam giác có 3 đỉnh là 3 trong 4 điểm trên. Viết tên các tam giác đó ?
Có bốn tam giác thỏa mãn yêu cầu đề bài, tên các tam giác đó là:
Tam giác ABC, tam giác CAD, tam giác BCD và tam giác ABD
Đúng 0
Bình luận (0)
Ta có 4 tam giác: Δ ABC, ΔABD, ΔBCD, ΔACD
Đúng 0
Bình luận (0)
Tồn tại hay không 5 điểm phân biệt trên mặt phẳng sao cho bất kì 3 điểm nào trong số 5 điểm đó cũng có 3 điểm là 3 đỉnh của một tam giác vuông
1. Trên mặt phẳng cho 2n điểm. Trong đó n điểm được tô màu đỏ và n điểm được tô màu xanh. CMR có ther kẻ được n đoạn thẳng, mỗi đầu mút được tô màu khác nhau và hai đoạn thẳng bất kỳ không có điểm chung,2. Trên mặt phẳng cho 25 điểm sao cho trong 3 điểm bất kì luôn có 2 điểm cách nhau một khoãng không vượt quá 1. Chúng minh rằng có đường ròn bán kính 1 chứa trong đó ít nhất 13 điểm3. Cho p là số nguyên tố lớn hơn 3 và n thuộc N*. CMR pn không thể là tổng lập phương của hai số dương4. Cho 10 điểm...
Đọc tiếp
1. Trên mặt phẳng cho 2n điểm. Trong đó n điểm được tô màu đỏ và n điểm được tô màu xanh. CMR có ther kẻ được n đoạn thẳng, mỗi đầu mút được tô màu khác nhau và hai đoạn thẳng bất kỳ không có điểm chung,
2. Trên mặt phẳng cho 25 điểm sao cho trong 3 điểm bất kì luôn có 2 điểm cách nhau một khoãng không vượt quá 1. Chúng minh rằng có đường ròn bán kính 1 chứa trong đó ít nhất 13 điểm
3. Cho p là số nguyên tố lớn hơn 3 và n thuộc N*. CMR pn không thể là tổng lập phương của hai số dương
4. Cho 10 điểm phân biệt không có 3 điểm nào thẳng hàng ằm trong một tam giac đều có cạnh bằng 2 cm. CMR luôn tìm được 3 điểm trong 10 điểm đã cho sao cho 3 đỉnh của 3 điểm này tạo thành 1 tam giac có diện tích không vượt quá\(\frac{\sqrt{3}}{3}cm^2\) và có một góc nhỏ hơn 45o
GIÚP MK NHA,MAI MK CẦN RỒI, GẤP LẮM NHA MÍ BẠN
Bài 1:Cho 10 điểm trong đó không có 3 điểm nào thẳng hàng. Có bao nhiêu tam giác mà các đỉnh là ba trong 10 điểm đó?
Bài 2:
Cho 25 điểm trong đó không có ba điểm nào thẳng hàng. Có bao nhiêu tam giác mà các đỉnh là ba trong 25 điểm đó?
Bài 1: Số hình tam giác là:
9+8+7+6+5+4+3+2+1= 45 (hình)
Bài 2: Số tam giác là:
24+23+...+2+1=300(hình)
Đúng 0
Bình luận (0)
bài 1 : số tam giác là [10*(10-1)*(10-2)]/2*3=120 ( tam giác)
bài 2: số tam giác là [25*24*23]/6=2300(tam giác)
Đúng 0
Bình luận (0)