Tham khảo:

tôi đăng câu hỏi lên để hỏi nếu mà biết tôi đã tự làm rồi

Gọi độ dài các cạnh của tam giác đó là a,b,c (a,b,c thuộc tập hợp Q)

Do các cạnh của tam giác đó tỉ lệ với 2;4;5 nên 

\(\frac{a}{2}=\frac{b}{4}=\frac{c}{5}\)và a+b+c=22 cm

Áp dụng tính chất của dãy tỉ số bằng nhau ta có

\(\frac{a}{2}=\frac{b}{4}=\frac{c}{5}=\frac{a}{2}+\frac{b}{4}+\frac{c}{5}=\frac{22}{11}=2\)

Do đó

\(\frac{a}{2}=2\Rightarrow a=4cm\)

\(\frac{b}{4}=2\Rightarrow b=8cm\)

\(\frac{c}{5}=2\Rightarrow c=10cm\)

Vậy độ dài các cạnh của tam giác đó lần lượt là 4;8;10 cm

Gọi độ dài các cạnh của 1 tam giác lần lượt là: x, y , z.

Ta có:

Độ dài các cạnh của tam giác tỉ lệ với các số 2;4;5 => x/2=y/4=z/5

x+y+z=22

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

x/2=y/4=z/5=x+y+z/2+4+5=22/11=2

x=4; y=8; z=10

Gọi x, y, z lần lượt là độ dài 3 cạnh của tam giác (cm, x, y, z > 0)

Vì các cạnh của tam giác tỉ lệ với các số 2,4 ; 5 nên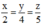 

Chu vi tam giác là 22 nên: x + y + z = 22.

Theo tính chất dãy tỉ số bằng nhau ta có:

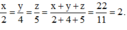
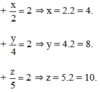
Vậy độ dài ba cạnh của tam giác lần lượt là 4cm, 8cm và 10cm.

Gọi độ dài ba cạnh của tam giác đó là a,b,c (a,b,c thuộc tập hợp Q)

Do 3 cạnh của tam giác tỉ lệ với 2,4,5 và chu vi là 22 cm  nên ta có

\(\frac{a}{2}=\frac{b}{4}=\frac{c}{5}\) và a+b+c=22 cm

Áp dụng tính chất của dãy tỉ số bằng nhau ta có

\(\frac{a}{2}=\frac{b}{4}=\frac{c}{5}=\frac{a}{2}+\frac{b}{4}+\frac{c}{5}=\frac{22}{11}=2\)

Do đó

\(\frac{a}{2}=2\Rightarrow a=4\)

\(\frac{b}{4}=2\Rightarrow b=8\)

\(\frac{c}{5}=2\Rightarrow c=10\)

Vậy độ dài ba cạnh lần lượt là 4cm,8cm,10cm

Gọi 3 cạnh tam giác là : a , b , c ( cm )

Theo bài ra ta có :

a/2 = b/4 = c/5

=> a/2 = b/4 = c/5 = a + b + c/2 + 4 + 5 = 22/11 = 2

=> a = 2 . 2 = 4 ( cm )

b = 4.2 = 8 ( cm )

c = 2 . 5 = 10

Tổng số phần bằng nhau là :

          2 + 4 + 5 = 11 (phần).

Giá trị 1 phần là :

          22 / 11 = 2 (cm).

Độ dài cạnh 1 là :

          2 * 2 = 4 (cm).

Độ dài cạnh 2 là :

          2 * 4 = 8 (cm).

Độ dài cạnh 3 là :

          2 * 5 = 10 (cm).

                  Đáp số : 4 cm, 8 cm,10 cm.

Gọi độ dài các cạnh là a;b;c (a;b;c > 0)

Áp dụng tính chất dãy tỉ số bằng nhau ta có

\(\frac{a}{2}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{2+4+5}=\frac{22}{11}=2\)

\(\Rightarrow a=4;b=8;c=10\)

Vậy độ dài các cạnh của tam giác là 4;8;10 cm

gọi 3 cạnh tam giác lần lượt là a;b;c

theo đề bài ta có

\(\frac{a}{2}=\frac{b}{4}=\frac{c}{5}\) và a+b+c=22

theo tính chất dãy tỉ số bằng nhau ta có

\(\frac{a}{2}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{2+4+5}=\frac{ 22}{11}=2\)

ta được

a/2=2                b/4=2                 c/5=2

a=2x2                b=2x4                c=2x5

a=4                    b=8                    c=10

vậy độ dài các cạnh tam giác lần lượt là 4cm,8cm,10cm

Các cạnh của một tam giác có số đo tỉ lệ với các số 3;5;7.Tính số đo mỗi cajnhcura tam giác đó, biết chu vi của nó là 40cm

Gọi 3 cạnh của tam giác lần lượt là x,y,z

Theo đề bài ta có:
\(\frac{x}{2}=\frac{y}{4}=\frac{z}{5}\)  và x+y+z=22

Áp dụng tc của dãy tir số bằng nhau ta có:

\(\frac{x}{2}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{2+4+5}=\frac{22}{11}=2\)

=> \(\begin{cases}x=4\\y=8\\z=10\end{cases}\)