Cho (O) kẻ điểm M nằm ngoài (O) kẻ hai tiếp tuyến MA , MB ( A,B là tiếp điểm ) .Gọi N là trung điểm MB , AN cắt (O) tại điểm thứ 2 là C , MC cắt (O) tại điểm thứ hai là D
a , c/m tứ giác NAOB nội tiếp
b, c/m MA' =MC.MD
c c/m AD // MB

Những câu hỏi liên quan
Bài 4: (3 điểm) Từ điểm M nằm ngoài (O,R), kẻ hai tiếp tuyến MA, MB tới đường tròn (A và
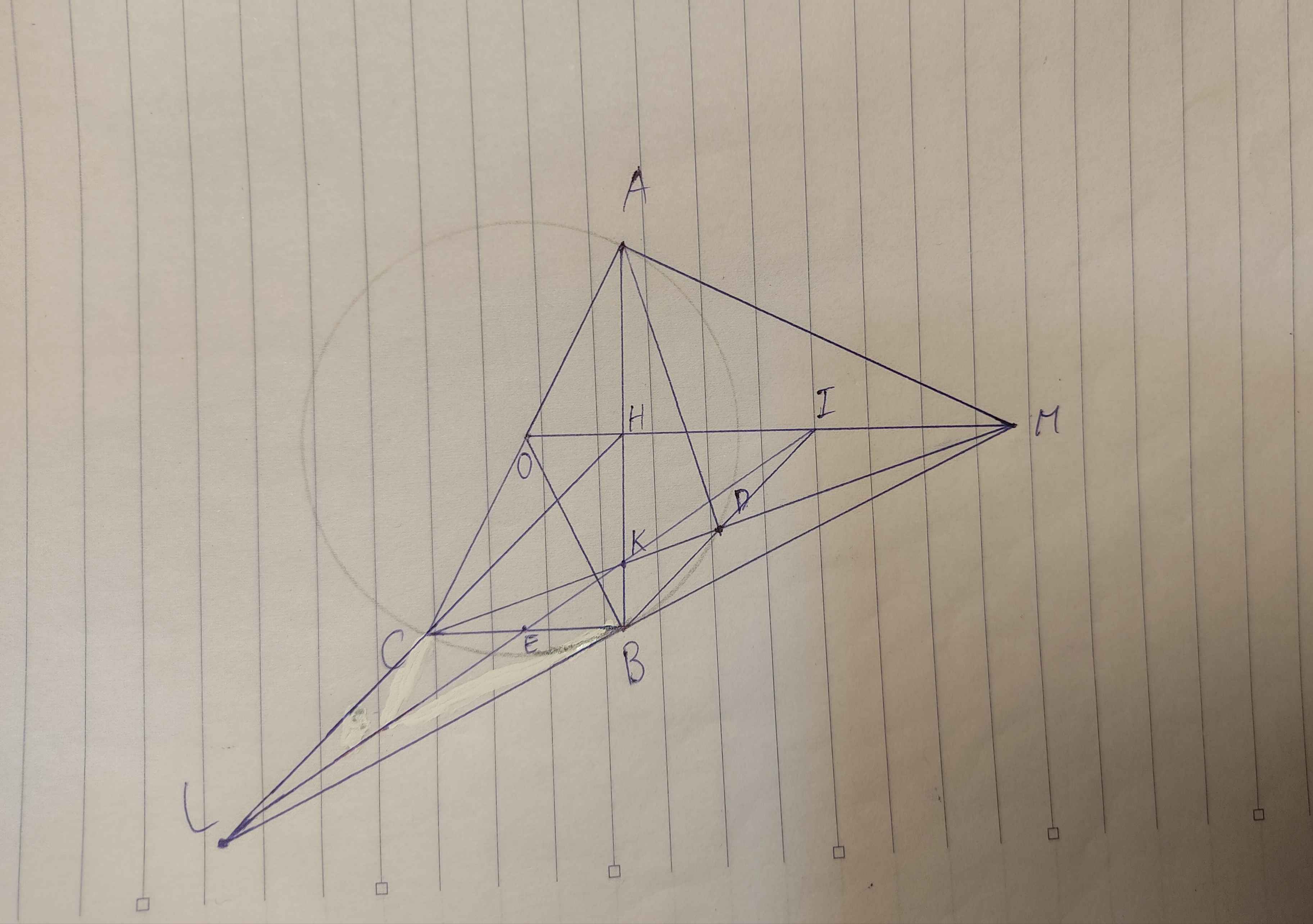
B là các tiếp điểm). Gọi N là trung điểm của MA; BN cắt (O) tại C. a/ Chứng minh: Tử giác MAOB nội tiếp và N * A ^ 2 =NB.NC . b/ Tia MC cắt (O) tại điểm thứ hai D. Chứng minh BD = AM. c/ Gọi I là trung điểm của CD; K là giao điểm của AB và CD, Chứng minh: MC .MD=MI.MK
Từ điểm M nằm ngoài đường tròn (O) kẻ 2 tiếp tuyến MA và MB với đường tròn (A,B là tiếp điểm). Lấy điểm C thuộc cung nhỏ AB sao cho cung CA nhỏ hơn cung CB, MC cắt đường tròn tại điểm thứ hai là D. Gọi H là trung điểm CD.
1. CM: tứ giác MAHO nội tiếp
2. Gọi K là giao điểm của AB và CD, chứng minh MH.MKMC.MD
3. Đường thẳng qua C song song với MB cắt AB tại E, DE cắt MB tại F, chứng minh F là trung điểm của BM
Xin hãy giúp mình ý 3 với, mình cảm ơn nhiều ❤
Đọc tiếp
Từ điểm M nằm ngoài đường tròn (O) kẻ 2 tiếp tuyến MA và MB với đường tròn (A,B là tiếp điểm). Lấy điểm C thuộc cung nhỏ AB sao cho cung CA nhỏ hơn cung CB, MC cắt đường tròn tại điểm thứ hai là D. Gọi H là trung điểm CD. 1. CM: tứ giác MAHO nội tiếp 2. Gọi K là giao điểm của AB và CD, chứng minh MH.MK=MC.MD 3. Đường thẳng qua C song song với MB cắt AB tại E, DE cắt MB tại F, chứng minh F là trung điểm của BM Xin hãy giúp mình ý 3 với, mình cảm ơn nhiều ❤
3: góc MHO=góc MAO=góc MBO=90 độ
=>M,A,O,H,B cùng nằm trên đường tròn đường kính OM
=>góc HAB=góc HMB
CE//MB
=>góc HCE=góc HMB=góc HAB
=>ACEH nội tiếp
=>góc CHE=góc CAE
mà góc CAE=góc CDB
nên gó CHE=góc CDB
=>HE//DB
Gọi K là giao của CE và DB
Xét ΔCKD có
H là trung điểm của CD
HE//KD
=>E là trung điểm của CK
=>EC=EK
Vì CK//MB
nên CE/MF=DE/DF=EK/FB
mà CE=EK
nên MF=FB
=>F là trung điểm của MB
Đúng 1
Bình luận (0)
Cho điểm M nằm ngoài đường tròn (O,R) từ điểm M kẻ hai tiếp tuyến MA, MB vớ đường tròn dó ( A,B là các tiếp điểm). Qua A kẻ đường thẳng song song MB cắt đường tròn (o) tại điểm C. Nối MC cắt đường tròn (O) tại D. Tia AD cắt MB tại E. CMR
a) MAOB là tứ giác nội tiếp
b)EM=EB
c) Xác định vị trí điểm M để BD vuông góc MA
Giúp mình câu c với ạ! Từ một điểm M nằm ngoài đường tròn(O) kẻ hai tiếp tuyến MA, MB đến đường trong (O) ( với A,B là các tiếp điểm). Vẽ đường kính AC. MC cắt đường trong (O) tại điểm thứ 2 là D. a, cm: tứ giác MAOB ntb, Gọi gđ của BD và MO là I. cm: MO//BC và IM2IB.IDc, Đonạ thẳng AB cắt MO và MC lần lượt tại H và K. tia HC cắt IK tại L. CMR: I là trung điểm MH và M,B,L thẳng hàng
Đọc tiếp
Giúp mình câu c với ạ!
Từ một điểm M nằm ngoài đường tròn(O) kẻ hai tiếp tuyến MA, MB đến đường trong (O) ( với A,B là các tiếp điểm). Vẽ đường kính AC. MC cắt đường trong (O) tại điểm thứ 2 là D.
a, cm: tứ giác MAOB nt
b, Gọi gđ của BD và MO là I. cm: MO//BC và IM2=IB.ID
c, Đonạ thẳng AB cắt MO và MC lần lượt tại H và K. tia HC cắt IK tại L. CMR: I là trung điểm MH và M,B,L thẳng hàng
Từ một điểm nằm ngoài đường tròn (O;R) kẻ 2 tiếp tuyến MA, MB (A, B là các tiếp điểm). Hai đường cao AE, BF của ΔAMB cắt nhau tại H.
a, C/m: Tứ giác ABEF là tứ giác nội tiếp
b, Gọi I là trung điểm của AB. C/m: 4 điểm O, H, I, M thẳng hàng
b) Xét (O) có
MA là tiếp tuyến có A là tiếp điểm(gt)
MB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: MA=MB(Tính chất hai tiếp tuyến cắt nhau)
Xét ΔMAB có MA=MB(cmt)
nên ΔMAB cân tại M(Định nghĩa tam giác cân)
Suy ra: \(\widehat{MAB}=\widehat{MBA}\)(hai góc ở đáy)
hay \(\widehat{FAB}=\widehat{EBA}\)
Xét ΔFAB vuông tại F và ΔEBA vuông tại E có
AB chung
\(\widehat{FAB}=\widehat{EBA}\)(cmt)
Do đó: ΔFAB=ΔEBA(cạnh huyền-góc nhọn)
Suy ra: \(\widehat{FBA}=\widehat{EAB}\)(hai góc tương ứng)
hay \(\widehat{HBA}=\widehat{HAB}\)
Xét ΔHAB có \(\widehat{HBA}=\widehat{HAB}\)(cmt)
nên ΔHAB cân tại H(Định lí đảo của tam giác cân)
Ta có: OA=OB(=R)
nên O nằm trên đường trung trực của AB(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: IA=IB(I là trung điểm của AB)
nên I nằm trên đường trung trực của AB(Tính chất đường trung trực của một đoạn thẳng)(2)
Ta có: HA=HB(ΔHAB cân tại H)
nên H nằm trên đường trung trực của AB(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: MA=MB(cmt)
nên M nằm trên đường trung trực của AB(Tính chất đường trung trực của một đoạn thẳng)(4)
Từ (1), (2), (3) và (4) suy ra O,H,I,M thẳng hàng(đpcm)
Đúng 1
Bình luận (0)
a) Xét tứ giác ABEF có
\(\widehat{AEB}=\widehat{AFB}\left(=90^0\right)\)
\(\widehat{AEB}\) và \(\widehat{AFB}\) là hai góc cùng nhìn cạnh AB
Do đó: ABEF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)
Cho điểm M nằm ngoài đường tròn (O ; R). Kẻ hai tiếp tuyến MA, MB với đường tròn ( A, B là tiếp điểm). QUa A kẻ đường thẳng song song với MB cắt (O) tại C. Nối MC cắt (O) tại D. Tia AD căst MB tại E.
a) Chứng minh: Tứ giác MAOB nội tiếp
b) Chứng minh: EM = EB
c) Xác định vị trí điểm M để BD vuông góc với MA
Cho điểm M nằm ngoài đường tròn (O ; R). Kẻ hai tiếp tuyến MA, MB với đường tròn ( A, B là tiếp điểm). QUa A kẻ đường thẳng song song với MB cắt (O) tại C. Nối MC cắt (O) tại D. Tia AD căst MB tại E.
a) Chứng minh: Tứ giác MAOB nội tiếp
b) Chứng minh: EM = EB
c) Xác định vị trí điểm M để BDvuông goc với MA
Cho điểm M nằm ngoài đường tròn (O ; R). Kẻ hai tiếp tuyến MA, MB với đường tròn ( A, B là tiếp điểm). QUa A kẻ đường thẳng song song với MB cắt (O) tại C. Nối MC cắt (O) tại D. Tia AD căst MB tại E.
a) Chứng minh: Tứ giác MAOB nội tiếp
b) Chứng minh: EM = EB
c) Xác định vị trí điểm M để BD\(⊥\)MA
từ điểm m nằm ngoài đường tròn (o) vẽ 2 tiếp tuyến ma mb gọi E là trung điểm cuả MB đường thẳng AE cắt (O) tại C,MC cắt (O) tại D ,H là giao điểm của AB và MO a) chứng minh HE// AM b) chứng minh tứ giác HCEB nội tiếp và AD // MBc) gọi F là giao điểm của BO và(O) K là giao điểm của AD và MF chứng minh KD =3KA