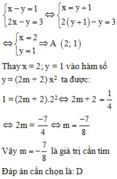cho hàm số y = ( 2m - 1 ) x2 với m # \(\frac{1}{2}\) tìm m để hàm số đồng biến khi x > 0

Những câu hỏi liên quan
a/ cho hàm số: y=(-3m - 2)x2. Tìm m để hàm số nghịch biến khi x < 0
b/ cho hàm số: y=(m2 - 2m + 3)x2. Xác định tính biến thiên của hàm số
c/ cho hàm số: y=(2m + 3)x2. Tìm m để hàm số đồng biến khi x>0
a.
Hàm số nghịch biến khi \(x< 0\Rightarrow-3m-2>0\Rightarrow m< -\dfrac{2}{3}\)
b.
Do \(a=m^2-2m+3=\left(m-1\right)^2+2>0;\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
c.
Hàm đồng biến khi \(x>0\Rightarrow2m+3>0\)
\(\Rightarrow m>-\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
Cho hàm số y = (m2 + 2m + 5)x2. Với giá trị nào của x thì :
a) Hàm số đồng biến.
b) Hàm số nghịch biến.
c) Với x = 1 thì y = 8. Tìm m
câu a và b thay số vào là ra nhé, bài mik hơi khác:
Ta có m^2 + 2m + 3 = m^2 + 2m + 1 + 2 = (m + 1)^2 + 2 > 0 với mọi m.
Suy ra hàm số đã cho đồng biến với mọi m với x > 0 và nghịch biến với x < 0
Đúng 0
Bình luận (0)
a) Vì \(m^2+2m+5>0\forall m\) nên để hàm số \(y=\left(m^2+2m+5\right)x^2\) đồng biến thì x>0
b) Vì \(m^2+2m+5>0\forall m\) nên để hàm số \(y=\left(m^2+2m+5\right)x^2\) nghịch biến thì x<0
c) Thay x=1 và y=8 vào hàm số \(y=\left(m^2+2m+5\right)x^2\), ta được:
\(m^2+2m+5=8\)
\(\Leftrightarrow m^2+2m-3=0\)
\(\Leftrightarrow m^2+3m-m-3=0\)
\(\Leftrightarrow m\left(m+3\right)-\left(m+3\right)=0\)
\(\Leftrightarrow\left(m+3\right)\left(m-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m+3=0\\m-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-3\\m=1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho hai hàm số : (P) y = \(x^2\) và (d) y = 2mx + 2m +1 với m là tham số
Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ x1,x2 sao cho
\(\sqrt{x1+x2}\) + \(\sqrt{3+x1.x2}\) = 2m + 1
Lời giải:
PT hoành độ giao điểm:
$x^2-2mx-(2m+1)=0(*)$
Để (P) và (d) cắt nhau tại 2 điểm pb có hoành độ $x_1,x_2$ thì PT $(*)$ phải có 2 nghiệm pb $x_1,x_2$
$\Leftrightarrow \Delta'=m^2+2m+1>0\Leftrightarrow (m+1)^2>0$
$\Leftrightarrow m\neq -1$
Áp dụng định lý Viet: $x_1+x_2=2m; x_1x_2=-(2m+1)$
Khi đó:
$\sqrt{x_1+x_2}+\sqrt{3+x_1x_2}=2m+1$
$\Leftrightarrow \sqrt{2m}+\sqrt{3-2m-1}=2m+1$
\(\Leftrightarrow \left\{\begin{matrix}
0\leq m< 1\\
\sqrt{2m}+\sqrt{2(1-m)}=2m+1\end{matrix}\right.\)
Bình phương 2 vế dễ dàng giải ra $m=\frac{1}{2}$ (thỏa)
Đúng 2
Bình luận (0)
a) (1- x2). ( 4x+5/x-1 - 9/x-1)b. x2 + xy - 2x - 2y Câu 5. Cho hàm số: y (2m+1)x - 3 a. Với m3. Tính f (-3); f(0) b. Tìm m để điểm A(2; 3) thuộc đồ thị hàm số. c. Vẽ đồ thị hàm số với m 1 d. Tìm điều kiện để hàm số là hàm bậc nhất. e. Tìm m để hàm số song song với đường thẳng y 5x+1
Đọc tiếp
a) (1- x2). ( 4x+5/x-1 - 9/x-1)
b. x2 + xy - 2x - 2y
Câu 5. Cho hàm số: y = (2m+1)x - 3
a. Với m=3. Tính f (-3); f(0)
b. Tìm m để điểm A(2; 3) thuộc đồ thị hàm số.
c. Vẽ đồ thị hàm số với m= 1
d. Tìm điều kiện để hàm số là hàm bậc nhất.
e. Tìm m để hàm số song song với đường thẳng y= 5x+1
Câu 5:
a: Khi m=3 thì \(f\left(x\right)=\left(2\cdot3+1\right)x-3=7x-3\)
\(f\left(-3\right)=7\cdot\left(-3\right)-3=-21-3=-24\)
\(f\left(0\right)=7\cdot0-3=-3\)
b: Thay x=2 và y=3 vào f(x)=(2m+1)x-3, ta được:
\(2\left(2m+1\right)-3=3\)
=>2(2m+1)=6
=>2m+1=3
=>2m=2
=>m=1
c: Thay m=1 vào hàm số, ta được:
\(y=\left(2\cdot1+1\right)x-3=3x-3\)
*Vẽ đồ thị
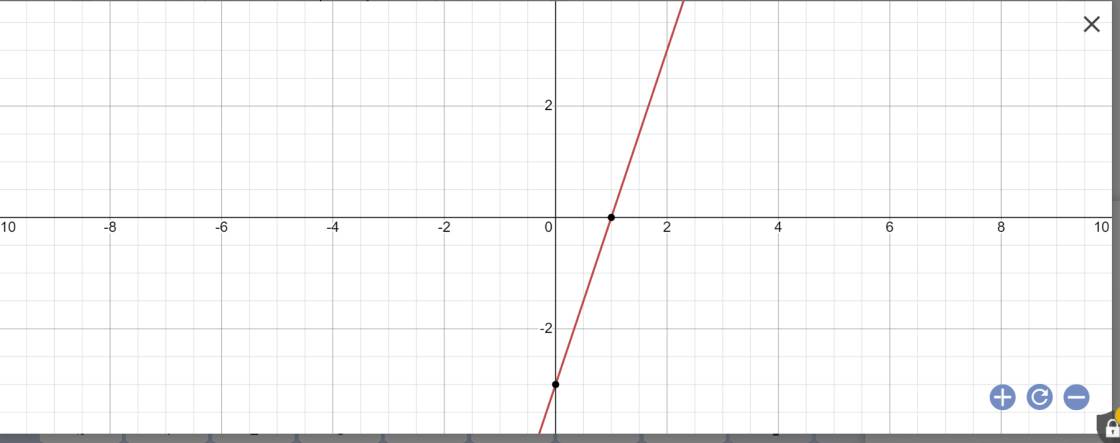
d: Để hàm số y=(2m+1)x-3 là hàm số bậc nhất thì \(2m+1\ne0\)
=>\(2m\ne-1\)
=>\(m\ne-\dfrac{1}{2}\)
e: Để đồ thị hàm số y=(2m+1)x-3 song song với đường thẳng y=5x+1 thì \(\left\{{}\begin{matrix}2m+1=5\\-3\ne1\end{matrix}\right.\)
=>2m+1=5
=>2m=4
=>m=2
Đúng 0
Bình luận (0)
Bài 1. Cho hàm số: y 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x 1Bài 2. Cho hàm số y 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x -2 .Bài 3. Cho hàm số y 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x 2.Bài 4. Tìm tất cả tham số thực m để hàm số y (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tạix -1.Bài 5. Tìm giá trị của tham số m để hàm số y x3/3...
Đọc tiếp
Bài 1. Cho hàm số: y = 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x = 1
Bài 2. Cho hàm số y = 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x = -2 .
Bài 3. Cho hàm số y = 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x = 2.
Bài 4. Tìm tất cả tham số thực m để hàm số y = (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tại
x = -1.
Bài 5. Tìm giá trị của tham số m để hàm số y = x3/3 +(2m - 1)x2 + (m - 9)x + 1 đạt cực tiểu tại
x = 2 .
Đừng hỏi tại sao tui ngu!!!
Giúp.com.vn
Với giá trị nào của m, hàm số
y
-
m
x
4
+
2
(
m
-
1
)
x
2
+
1
-
2
m
có một cực trị A.0 ≤ m ≤ 1 B. m 1 hoặc m 0 C. 0 m 1 D. 0 m ≤ 1
Đọc tiếp
Với giá trị nào của m, hàm số y = - m x 4 + 2 ( m - 1 ) x 2 + 1 - 2 m có một cực trị
A.0 ≤ m ≤ 1
B. m > 1 hoặc m < 0
C. 0 < m < 1
D. 0 < m ≤ 1
Chọn A
Xét hàm số y = - m x 4 + 2 ( m - 1 ) x 2 + 1 - 2 m ( 1 )
TH1: m = 0 (1) trở thành y = -2x2 + 1
Vậy với m = 0 hàm số luôn có một cực trị.
TH2: m ≠ 0. y ' = - 4 m x 3 + 4 ( m - 1 ) x
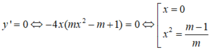
Để hàm số (1) có một cực trị thì
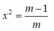
vô nghiệm hoặc có nghiệm kép bằng 0

Kết hợp cả hai trường hợp ta có 0 ≤ m ≤ 1
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
+
2
m
−
2
x
2
−
5
x
+
1
. Tìm tất cả các giá trị thực của tham số m sao cho hàm số có hai điểm cực trị
x
1
,
x
2
(
x
1...
Đọc tiếp
Cho hàm số y = x 3 + 2 m − 2 x 2 − 5 x + 1 . Tìm tất cả các giá trị thực của tham số m sao cho hàm số có hai điểm cực trị x 1 , x 2 ( x 1 < x 2 ) thỏa mãn x 1 − x 2 = − 2 .
A. 7 2
B. ‒1
C. 1 2
D. 5
Đáp án C.
Ta có y ' = 3 x 2 + 4 m − 2 x − 5 ; y ' = 0 ⇔ 3 x 2 + 4 m − 2 x − 5 = 0 (*).
Phương trình (*) có a c < 0 nên luôn có hai nghiệm trái dấu .
Suy ra x 1 = − x 1 ; x 2 = x 2 .
Khi đó x 1 , x 2 là hai điểm cực trị của hàm số.
x 1 − x 2 = − 2 ⇔ − x 1 − x 2 = − 2 ⇔ x 1 + x 2 = 2 ⇔ − 4 m − 2 3 = 2 ⇔ m = 1 2
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
+
2
m
−
2
x
2
−
5
x
+
1
. Tìm tất cả các giá trị thực của tham số m sao cho hàm số có hai điểm cực trị
x
1
,
x
2
(
x
1...
Đọc tiếp
Cho hàm số y = x 3 + 2 m − 2 x 2 − 5 x + 1 . Tìm tất cả các giá trị thực của tham số m sao cho hàm số có hai điểm cực trị x 1 , x 2 ( x 1 < x 2 ) thỏa mãn x 1 − x 2 = − 2 .
A. 7 2
B. ‒1
C. 1 2
D. 5
Cho hàm số
y
(
2
m
+
2
)
x
2
. Tìm m để đồ thị hàm số đi qua điểm A (x; y) với (x: y) là nghiệm của hệ phương trình:
x
−
y
1
2
x...
Đọc tiếp
Cho hàm số y = ( 2 m + 2 ) x 2 . Tìm m để đồ thị hàm số đi qua điểm A (x; y) với (x: y) là nghiệm của hệ phương trình: x − y = 1 2 x − y = 3
A. m = 7 4
B. m = 1 4
C. m = 7 8
D. m = - 7 8
Hàm số y mx4 + (m + 3)x2 + 2m – 1 chỉ đạt cực đại mà không có cực tiểu với m A. m 3 . B. m ≤ -3 C. m ≤ 0 hoặc m 3 D. -3 m 0
Đọc tiếp
Hàm số y = mx4 + (m + 3)x2 + 2m – 1 chỉ đạt cực đại mà không có cực tiểu với m
A. m > 3 .
B. m ≤ -3
C. m ≤ 0 hoặc m >3
D. -3 < m < 0
Đáp án B.
Với m = 0, hàm số đã cho là parabol y = 3x2 – 1 chỉ có cực tiểu. Vậy m = 0 không thỏa mãn
Với m ≠ 0, hàm số đã cho là một hàm trùng phương.
Dựa vào đồ thị, muốn hàm số chỉ có cực đại mà không có cực tiểu thì hàm số chỉ có một cực trị, muốn đó là cực đại thì 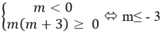
Đúng 0
Bình luận (0)