giúp mình với 10p nữa mình phải nộp bài rồi

Những câu hỏi liên quan
Ai giúp mình bài này với. 15p nữa mình phải nộp rồi :(
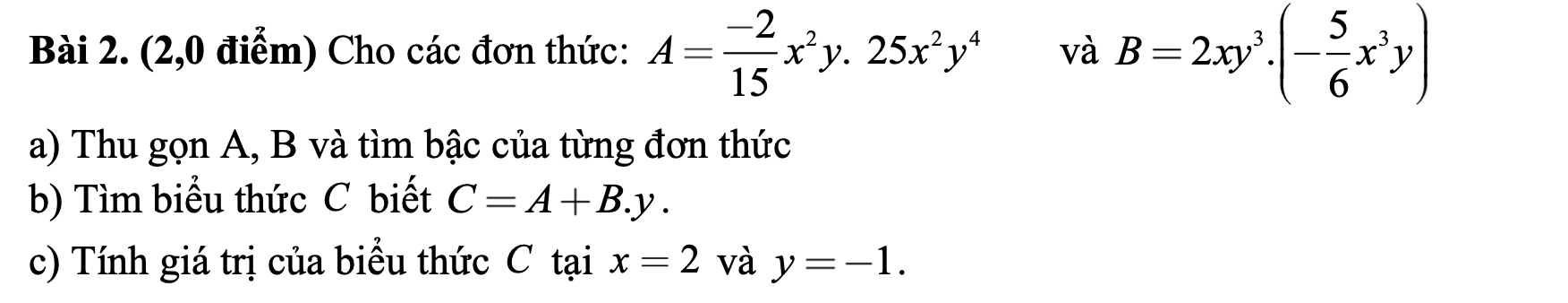
a: A=-2/15*25*x^2y*x^2y^4=-10/3*x^4y^5
B=2*(-5/6)*xy^3*x^3y=-5/3*x^4y^4
b: C=A+B*y
=-10/3*x^4y^5-5/3*x^4y^5
=-5x^4y^5
c: Khi x=2 và y=-1 thì C=-5*2^4*(-1)^5=5*16=80
Đúng 0
Bình luận (0)
Các bạn làm giúp mình mấy bài này 1 tiếng nữa là mình phải nộp rồi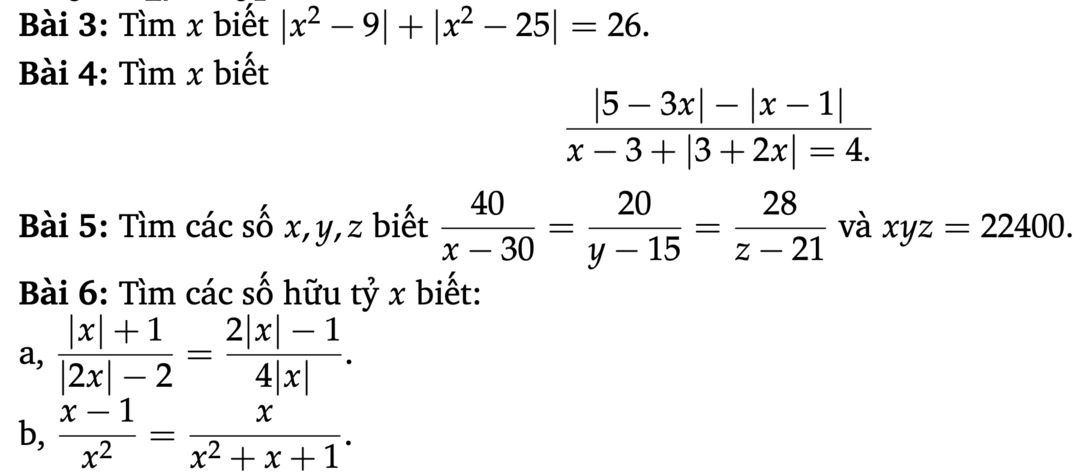
Bài 5:
\(\dfrac{40}{x-30}=\dfrac{20}{y-15}=\dfrac{28}{z-21}\\ \Rightarrow\dfrac{x-30}{40}=\dfrac{y-15}{20}=\dfrac{z-21}{28}=k\\ \Rightarrow\dfrac{x}{40}-\dfrac{3}{4}=\dfrac{y}{20}-\dfrac{3}{4}=\dfrac{z}{28}-\dfrac{3}{4}\\ \Rightarrow\dfrac{x}{40}=\dfrac{y}{20}=\dfrac{z}{28}=k\left(đặt.k\right)\\ \Rightarrow x=40k;y=20k;z=28k\)
Mà \(xyz=22400\Rightarrow22400k^3=22400\)
\(\Rightarrow k^3=1\Rightarrow k=1\Rightarrow\left\{{}\begin{matrix}x=40\\y=20\\z=28\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Moị người ơi giúp mình với chỉ cho mình cách tìm UCLN đi,4 ngày nữa mình phải nộp bài rồi mà không biết làm thế nào
Cách tìm ước chung lớn nhất:
Muốn tìm ƯCLN của hai hay nhiều số, ta thực hiện ba bước sau:
Bước 1: Phân tích mỗi thừa số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung.
Bước 3: Lập tích các thừa số chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm.
Đúng 0
Bình luận (0)
Phân tích thành thừa số nguyên tố rồi từ đó lấy các thừa số chung với mũ lớn nhất là tìm được UCLN nha bạn
Đúng 0
Bình luận (0)
Ước chung lớn nhất của a và b được ký hiệu là ƯCLN(a, b), hay đơn giản hơn là (a, b). Tiếng Anh: greatest common factor hoặc greatest common divisor(GCD hoặc GCF). Chẳng hạn, ƯCLN(12, 18) = 6, ƯCLN(−4, 14) = 2 & ƯCLN(5, 0) = 5. Hai số được gọi là nguyên tố cùng nhau nếu ước chung lớn nhất của chúng bằng 1. Chẳng hạn, 9 và 28 là nguyên tố cùng nhau.
Ước chung lớn nhất được sử dụng để đưa một phân số về dạng phân số tối giản. Chẳng hạn, ƯCLN(42, 56)=14, do đó,
{\displaystyle {42 \over 56}={3\cdot 14 \over 4\cdot 14}={3 \over 4}.}
Các tính chất[sửa | sửa mã nguồn]
Mọi ước chung của a và b là ước của ƯCLN(a, b).Bước 0 29 8 5 3 1 0 1 0 1 -3 1 8 5 3 1 0 1 -1 1 -3 4 2 5 3 2 1 1 -1 2 -3 4 -7 3 3 2 1 1 -1 2 -3 4 -7 11 4 2 1 0 2
ƯCLN(a, b), khi a và b không bằng không cả hai, có thể được định nghĩa tương đương như số nguyên dương d nhỏ nhất có dạng d = a·p + b·q trong đó p và q là các số nguyên. Định lý bày được gọi là đẳng thức Bézout. Các số p và qcó thể tính nhờ Giải thuật Euclid mở rộng.ƯCLN(a, 0) = |a|, với mọi a ≠ 0, vì mọi số khác không bất kỳ là ước của 0, và ước lớn nhất của a là |a|. Đây là trường hợp cơ sở trong thuật toán Euclid.Nếu a là ước của tích b·c, và ƯCLN(a, b) = d, thì a/d là ước của c.Nếu m là số nguyên dương, thì ƯCLN(m·a, m·b) = m·ƯCLN(a, b).Nếu m là số nguyên bất kỳ, thì ƯCLN(a + m·b, b) = ƯCLN(a, b). Nếu m ước chung (khác 0) của a và b, thì UCLN(a/m, b/m) = ƯCLN(a, b)/m.ƯCLN là một hàm có tính nhân theo nghĩa sau: nếu a1 và a2 là nguyên tố cùng nhau, thì ƯCLN(a1·a2, b) = ƯCLN(a1, b)·ƯCLN (a2, b).ƯCLN là hàm giao hoán: ƯCLN(a, b) = ƯCLN(b, a).ƯCLN là hàm kết hợp: ƯCLN(a, ƯCLN(b, c)) = ƯCLN(ƯCLN(a, b), c).ƯCLN của ba số được tính nhờ công thức ƯCLN(a, b, c) = ƯCLN(ƯCLN(a, b), c), (hoặc vế kia của tính chất kết hợp. Điều này có thể mở rộng cho số bất kỳ các số nguyên.ƯCLN (a, b) quan hệ chặt chẽ với BCNN(a, b): ta cóƯCLN(a, b)·BCNN(a, b) = a·b.
Công thức này thường được dùng để tính BCNN. Dạng khác của mối quan hệ này là tính chất phân phối:
(a, b), ƯCLN(a, c))
BCNN(a, ƯCLN(b, c)) = ƯCLN(BCNN(a, b), BCNN(a, c)).
Nếu sử dụng định nghĩa ƯCLN(0, 0) = 0 và BCNN(0, 0) = 0 thì khi đó tập các số tự nhiên trở thành một dàn đầy đủ phân phối với ƯCLN.Trong Hệ tọa độ Descartes, ƯCLN(a, b) biểu diễn số các điểm với tọa độ nguyên trên đoạn thẳng nối các điểm (0, 0) và (a, b), trừ chính điểm (0, 0).Tính ước chung lớn nhất[sửa | sửa mã nguồn]
ƯCLN của hai số có thể tìm được bằng việc phân tích hai số đó ra thừa số nguyên tố, chẳng hạn để tìm ƯCLN(18,84), ta phân tích 18 = 2·32 và 84 = 22·3·7 và nhận xét rằng các thừa số chung với số mũ dương nhỏ nhất của hai số này là 2·3; do đó ƯCLN(18,84) = 6. Trên thực tế phương pháp này chỉ dùng cho các số nhỏ; việc phân tích các số lớn ra thừa số nguyên tố mất rất nhiều thời gian.
Một phương pháp hiệu quả là giải thuật Euclid dựa trên dãy liên tiếp các phép chia có dư.
Nếu a và b là các số khác không, thì ước chung lớn nhất của a và b có thể tính qua bội chung nhỏ nhất (BCNN) của a và b:
{\displaystyle UCLN(a,b)={\frac {a\cdot b}{BCNN(a,b)}}}
Cách tìm ƯCLN trong lập trình C#:sta int USCLN(int a, int b) { a=Math.Abs(a); b=Math.Abs(b); if (a==0 ||b==0) return a+b; while (a!=b) { if(a>b) a=a-b; else b=b-a; } return a; }
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giúp mình với 3 tiếng nữa mình phải nộp cho cô rồi!!! Please 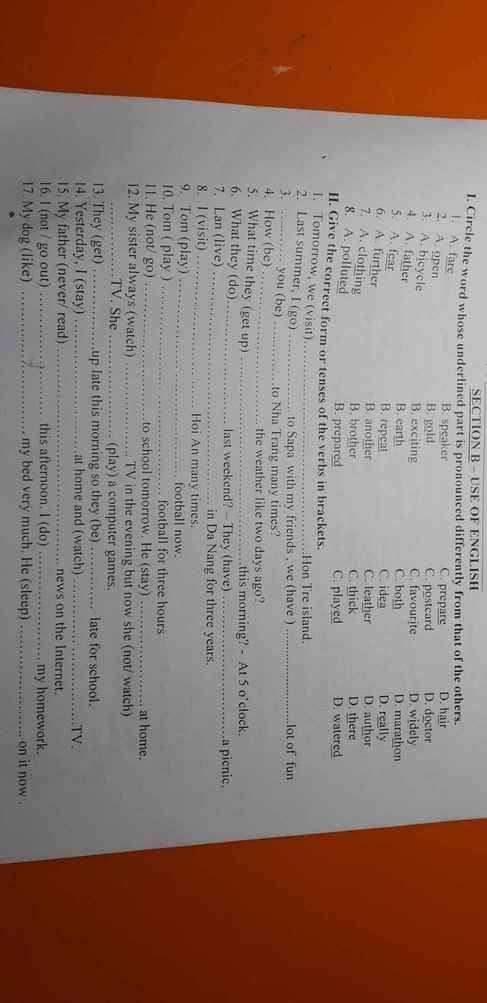

I
1 B
2 A
3 C
4 A
5 B
6 D
7 C
8 A
II
1 are going to visit
2 went - had - have you been
3 was
5 do they get up
6 did they do - had
7 has lived
8 have visited
9 is playing
10 has played
11 won't go - will stay
12 watches - isn't watching - is playing
13 got - were
14 stayed - watched
15 has never read
16 won't go - will do
17 likes - is sleeping
18 inviting
19 is
20 is
Đúng 2
Bình luận (1)
III
1 B
2 A
3 D
4 B
5 A
6 A
7 C
8 B
9 C
10 C
11 A
12 B
13 B
14 D
15 C
16 B
17 D
18 B
19 D
20 D
21 A
22 A
23 C
Đúng 2
Bình luận (0)
Các bạn làm giúp mình mấy bài này 1 tiếng nữa là mình phải nộp rồi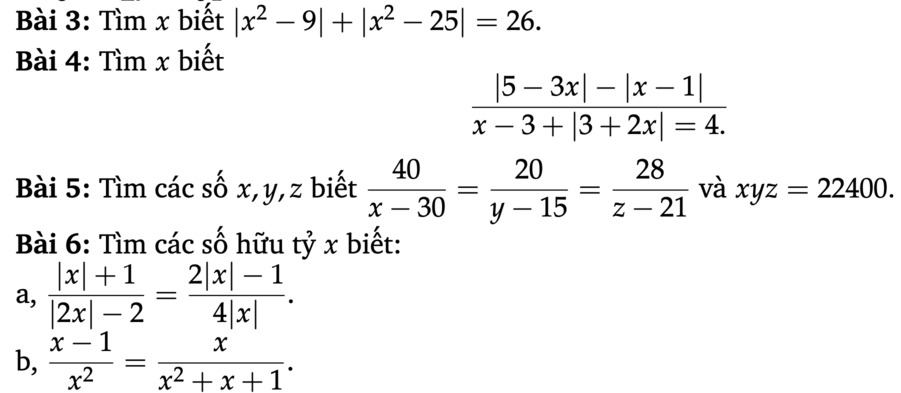 (mình sẽ tích cho tất cả các bạn)
(mình sẽ tích cho tất cả các bạn)
Mn giúp mình gấp với , 10p nữa là kt rồi 😭😭😭





Giúp mình bài 7 với . Mai mình phải nộp rồi.
Bài 7:
\(\widehat{AOB}+\widehat{A}+\widehat{B}=360^0\)
nên Ax//By
Đúng 0
Bình luận (0)
Bạn nào giúp mình làm bài này với 1 tiếng nữa là mình phải nộp rôi
Bạn nào giúp mình làm bài này với 1 tiếng nữa là mình phải nộp rôi














