a)x² + 12x + 36 =(x + 6)²    
2 + 81 + 18x =(x + 9)²
2- 16x + 64 =(x - 8)²
2

a)x²+12x+.36..=(..x+6..)²    
b)x²+81+.18x..=(..x+9..)²
c)x²-16x+.64..=(..x-8..)²
d)16-2x+...=(....)²

Câu cuối có bị lỗi không nhỉ ?

\(a,...+....36=\left(x-6\right)^2\)

\(b,....+1640,25=\left(x+40,5\right)^2\)

\(c,....+64=\left(x-8\right)^2\)

\(d,...+\left(\dfrac{1}{16}x\right)^2=\left(4-\dfrac{1}{4}x\right)^2\)

\(a,\Leftrightarrow x\left(x+9\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-9\end{matrix}\right.\\ b,\Leftrightarrow\left(x+4-4\right)\left(x+4+4\right)=0\\ \Leftrightarrow x\left(x+8\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-8\end{matrix}\right.\\ c,\Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\\ d,\Leftrightarrow\left(x-5\right)^2=0\Leftrightarrow x=5\)

a) \(\Leftrightarrow x\left(x+9\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-9\end{matrix}\right.\)

b) \(\Leftrightarrow x\left(x+8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-8\end{matrix}\right.\)

c) \(\Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)

d) \(\Leftrightarrow\left(x-5\right)^2=0\\ \Leftrightarrow x=5\)

ĐKXĐ: x>=1

\(PT\Leftrightarrow8\sqrt{x-1}+7\sqrt{x-1}-\sqrt{x-1}=46\)

=>\(14\sqrt{x-1}=46\)

=>\(\sqrt{x-1}=\dfrac{23}{7}\)

=>\(x-1=\dfrac{529}{49}\)

=>\(x=\dfrac{578}{49}\)

2\(\sqrt{1\text{6}x-1\text{6}}\)+\(\sqrt{49x-49}\)-\(\sqrt{x-1}\)=46

<=>2.4.4\(\sqrt{x-1}\)+7.7\(\sqrt{x-1}\)-\(\sqrt{x-1}\)=46

<=> 32\(\sqrt{x-1}\)+49\(\sqrt{x-1}\)-\(\sqrt{x-1}\)=46

<=> (32+49-1)\(\sqrt{x-1}\)=46

<=> 80\(\sqrt{x-1}\)=46

<=> \(\sqrt{x-1}\)=\(\dfrac{23}{40}\)

<=> x-1=\(\dfrac{529}{1\text{6}00}\)

<=> x=\(\dfrac{2159}{1\text{6}00}\)

<=>x=1,35

3: \(x^3+3x^2-16x-48\)

\(=x^2\left(x+3\right)-16\left(x+3\right)\)

\(=\left(x+3\right)\left(x-4\right)\left(x+4\right)\)

help

TXĐ: R

y′ = 16 + 4x − 16 x 2  − 4 x 3  = −4(x + 4)( x 2  − 1)

y' = 0 ⇔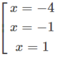 

Bảng biến thiên:

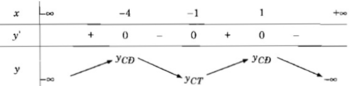
Vậy hàm số y đã cho đồng biến trên các khoảng (- ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )

a) TXĐ: R

y′ = 6x − 24 x 2  = 6x(1 − 4x)

y' = 0 ⇔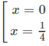 

y' > 0 trên khoảng (0; 1/4) , suy ra y đồng biến trên khoảng (0; 1/4)

y' < 0 trên các khoảng ( - ∞ ; 0 ); (14; + ∞ ), suy ra y nghịch biến trên các khoảng ( - ∞ ;0 ); (14; + ∞ )

b) TXĐ: R

y′ = 16 + 4x − 16 x 2  − 4 x 3  = −4(x + 4)( x 2  − 1)

y' = 0 ⇔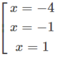 

Bảng biến thiên:

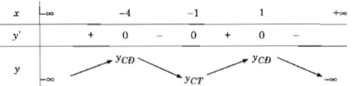
Vậy hàm số y đã cho đồng biến trên các khoảng ( - ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )

c) TXĐ: R

y′ = 3 x 2 − 12x + 9

y' = 0

y' > 0 trên các khoảng ( - ∞ ; 1), (3;  + ∞ ) nên y đồng biến trên các khoảng ( - ∞ ; 1), (3;  + ∞ )

y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)

d) TXĐ: R

y′ = 4 x 3  + 16 = 4x( x 2  + 4)

y' = 0 ⇔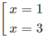 

y' > 0 trên khoảng (0;  + ∞ ) ⇒ y đồng biến trên khoảng (0;  + ∞ )

y' < 0 trên khoảng ( - ∞ ; 0) ⇒ y nghịch biến trên khoảng ( - ∞ ; 0)

Bạn ơi mk làm 3 phần a,b,c rồi đấy, bạn vào xem đi

Chúc bạn học tốt!

Lời giải:

$x^2=4.4.4.4=16.16=(-16)(-16)=16^2=(-16)^2$

$\Rightarrow x=16$ hoặc $x=-16$.