Cho tam giác ABC cân tại A . Trên cạnh AB,AC lần lượt lấy các điểm K,H sao cho AK=AH.GỌI O là giao điểm của BH và CK.Chứng minh tam giác OCB cân. (kèm theo hình ạ)
Mình đang cần gấp bạn nào giải nhanh,đúng thì mình tick cho ạ

Những câu hỏi liên quan
Cho tam giác ABC cân tại A . Trên cạnh AB,AC lần lượt lấy các điểm K,H sao cho AK=AH.GỌI O là giao điểm của BH và CK.Chứng minh tam giác OCB cân. (kèm theo hình ạ)
Mình đang cần gấp bạn nào giải nhanh,đúng thì mình tick cho ạ
Vì tam giác ABC cân tại A, nên ta có AB = AC.
Với AK = AH và AB = AC, ta có tam giác AKH cân tại A.
Gọi M là trung điểm của KH, ta có AM song song với BC và AM = 1/2 BC.
Ta thấy rằng tam giác BOM và COM đều có cạnh ON (với N là trung điểm BC), BM = MC và góc BOM = 180° - góc COM.
Như vậy, tam giác BOC cân tại O vì OB = OC (cùng là đường trung bình trong tam giác đều BOC) và góc BOC = 2 × góc BOM = 2× (90° – 1/2 × góc MBC) = 180° – góc MBC = góc BOC (vì tam giác BOC cân tại O).
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A có góc A<90°.Kẻ BH vuông góc với AC(H thuộc AC).Trên canh AB lấy điểm K sao cho AK=AH.Gọi O là giao điểm của BH và CK.Chứng minh:
a)KH//BC
b)CK vuông góc với AB
c)AO là trung trực của BC
Cho tam giác ABC cân tại A lấy điểm H thuộc AC, đ iểm K thuộc AB. Sao cho AH=AK, Gọi O là giao điểm của BH và CK.Chứng minh: tam giác OBC là tam giác cân
Xét tam giác ABH và ACK có:
AH=AK(gt)
AB=AC(tam giác ABC cân)
Â:góc chung
=> ABH=ACK
=> Góc ABH= Góc ACK
=> Góc OBC= Góc OCB
=> OBC cân tại O
Đúng 0
Bình luận (0)
Ta có tam giác ABC là tam giác cân tại A AB=AC; B=C (tính chất tam giác cân) Xét tam giác ACK và tam giác ABH có: AK=AH(giả thiết) A chung AC=AB(giả thiết) => tam giác ACK=tam giác ABH(c.g.c) OBC=OCB(2 góc tương ứng) Ta có B=OBC + KBO C=OCB + HCO Mà B=C(giả thiết) KBO= HCO(cmt) => OBC= OCB => OBC là tam giác cân
Đúng 0
Bình luận (0)
Bài toán: Cho tam giác ABC cân tại A. Lấy điểm H thuộc cạnh AC, điểm K thuộc cạnh AB sao cho AH=AK. Gọi O là giao điểm của BH và CK. Chứng minh rằng tam giác OBC là tam giác cân
CÁC BẠN GIÚP MÌNH VS MÌNH ĐG CẦN GẤP
CÁC GIÚP MÌNH GIẢI CHI TIẾT LUN NHA
CẢM ƠN CÁC BẠN NHÌU !
Vì tam giác ABC cân tại A
=> Góc ABC=ACB
=> AB=AC ( t/c tam giác cân) (1)
Mà AH=AK ( gt) (2)
Và AH+HC=AC; AK+KB=AB (3)
Từ (1)(2)(3) => HC = KB
Xét tam giác KBC và HCB có:
BC chung
Góc ABC=ACB ( chứng minh trên)
KB=HC ( chứng minh trên)
=> Tam giác KBC=HCB ( c.g.c )
=> Góc KCB=HBC
Hay tam giác OBC cân tại O
Đúng 0
Bình luận (0)
xin loi minh ko biet nha bn
xin loi minh ko biet nha bn
xin loi minh ko biet nha bn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC cân tại A.Lấy điểm H thuộc cạnh AC,điểm K thuộc cạnh AB sao cho AH=AK.Gọi O là giao điểm của BH và CK.Chứng minh tam giác OBC là tam giác cân
Xét ΔHBC và ΔKCB có
HC=KB
\(\widehat{HCB}=\widehat{KBC}\)
BC chung
Do đó: ΔHBC=ΔKCB
Suy ra: \(\widehat{HBC}=\widehat{KCB}\)
=>\(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
Đúng 2
Bình luận (0)
Cho tam giác abc cân tại A. Lấy điểm H thuộc cạnh AC và điểm K thuộc cạnh AB sao cho AH=AK. Gọi O là giao điểm của BH và Ck. Chứng minh rằng tam giác OBC cân ( giải 2 cách giùm mình nha)
Cho tam giác ABC cân tại A. Lấy điểm H thuộc cạnh AC, điểm K thuộc cạnh AB sao cho AH = AK. Gọi O là giao điểm của BH và CK. Chứng minh rằng ΔOBClà tam giác cân.
+) Xét ΔABH và ΔACK, ta có:
AB = AC ( vì tam giác ABC cân tại A)
AH = AK (giả thiết)
Suy ra: ΔABH = ΔACK(c.g.c)

+ Do đó, tam giác OBC cân tại O.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có góc A < 90°.Kẻ BH vuông góc với AC.Trên cạnh AB lấy điểm K sao cho AK = AH.Gọi là giao điểm của BH và CK.Chứng minh:
a)KH // BC
b)CK vuông góc với AB
c)AO là trung trực của AB
Cho tam giác ABC cân tại A. Lấy điểm H thuộc cạnh AC, điểm K thuộc canh AB sao cho AH = AK. Gọi O là giao điểm của BH và CK. Chứng minh rằng tam giác OBC là tam giác cân ?
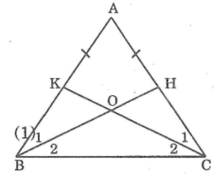
Hình vẽ:
Giải:
Xét \(\Delta ABH\) và \(\Delta ACK\) có:
\(AH=AK\left(gt\right)\)
\(\widehat{A}\) là góc chung
\(AB=AC\) ( Vì \(\Delta ABC\) cân tại \(A\) )
Do đó: \(\Delta ABH=\Delta ACK\left(c.g.c\right)\)
\(\Rightarrow\widehat{B_2}=\widehat{C_2}\) ( cặp góc tương ứng )
Mà \(\widehat{B}=\widehat{C}\) ( Do \(\Delta ABC\) cân tại \(A\) )
\(\Rightarrow\widehat{B}-\widehat{B_2}=\widehat{C}-\widehat{C_2}\)
\(\Rightarrow\widehat{B_1}=\widehat{C_1}\)
\(\Rightarrow\Delta OBC\) cân tại \(O\) . \(\left(đpcm\right)\)
Đúng 1
Bình luận (0)






















