tìm các nghiệm tự nhiên(x , y) của phương trình:
(x2 + 4x4 +28)2 = 17( x4 + y4 +14x2 +49)
\(\left(x^2+4y^2+28\right)^2=17\left(x^4+y^4+14y^2+49\right)\)
Tìm các nghiệm tự nhiên (x,y) của phương trình
\(\left(x^2+4z\right)^2=17\left(x^4+z^2\right)\)
\(x^4+8x^2z+16z^2=17x^4+17z^2\)
\(t^4-2t^2z+z^2=\left(t^2-z\right)^2=0\)
Nghiệm duy nhất: \(t^2=z\Rightarrow t^2=y^2+7\Rightarrow\hept{\begin{cases}t=4\Rightarrow x=2\\y=3\end{cases}}\)KL (x,y)=(2,3)
6) x2 + 2xy + y2 - x - y - 12
7) (x + 2)(x +3)(x + 4)(x + 5) - 24
8) 4x4 - 32x2 + 1
9) 3(x4 + x2 + 1) - (x2 + x + 1)2
10) 64x4 + y4
6) Ta có: \(x^2+2xy+y^2-x-y-12\)
\(=\left(x+y\right)^2-\left(x+y\right)-12\)
\(=\left(x+y-4\right)\left(x+y+3\right)\)
7) Ta có: \(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24\)
\(=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\)
\(=\left(x^2+7x\right)^2+22\left(x^2+7x\right)+120-24\)
\(=\left(x^2+7x\right)^2+22\left(x^2+7x\right)+96\)
\(=\left(x^2+7x+6\right)\left(x^2+7x+16\right)\)
\(=\left(x+1\right)\left(x+6\right)\left(x^2+7x+16\right)\)
8) Ta có: \(4x^4-32x^2+1\)
\(=4x^4+12x^3+2x^2-12x^3-36x^2-6x+2x^2+6x+1\)
\(=2x^2\left(2x^2+6x+1\right)-6x\left(2x^2+6x+1\right)+\left(2x^2+6x+1\right)\)
\(=\left(2x^2+6x+1\right)\left(2x^2-6x+1\right)\)
9) Ta có: \(3\left(x^4+x^2+1\right)-\left(x^2+x+1\right)^2\)
\(=3\left[x^4+2x^2+1-x^2\right]-\left(x^2+x+1\right)^2\)
\(=3\left(x^2-x+1\right)\left(x^2+x+1\right)-\left(x^2+x+1\right)^2\)
\(=\left(x^2+x+1\right)\left(3x^2-3x+3-x^2-x-1\right)\)
\(=\left(x^2+x+1\right)\left(2x^2-4x+2\right)\)
\(=2\left(x-1\right)^2\cdot\left(x^2+x+1\right)\)
Phân tích các đa thức sau thành nhân tử:
1) x3 - 7x + 6
2) x3 - 9x2 + 6x + 16
3) x3 - 6x2 - x + 30
4) 2x3 - x2 + 5x + 3
5) 27x3 - 27x2 + 18x - 4
6) x2 + 2xy + y2 - x - y - 12
7) (x + 2)(x +3)(x + 4)(x + 5) - 24
8) 4x4 - 32x2 + 1
9) 3(x4 + x2 + 1) - (x2 + x + 1)2
10) 64x4 + y4
11) a6 + a4 + a2b2 + b4 - b6
12) x3 + 3xy + y3 - 1
13) 4x4 + 4x3 + 5x2 + 2x + 1
14) x8 + x + 1
15) x8 + 3x4 + 4
16) 3x2 + 22xy + 11x + 37y + 7y2 +10
17) x4 - 8x + 63
1) \(x^2-7x+6=x^3+1-7x-7=\left(x^3+1\right)-7\left(x+1\right)=\left(x+1\right)\left(x^2-x-6\right)\)
2) \(x^3-9x^2+6x+16\)
\(\left(x^3+1\right)-\left[\left(9x^2-6x+1\right)-16\right]\)
\(=\left(x^3+1\right)-\left[\left(3x-1\right)^2-16\right]=\left(x^3+1\right)-\left(3x-1+4\right)\left(3x-1-4\right)\)\(=\left(x^3+1\right)-3\left(3x-5\right)\left(x+1\right)\)\(=\left(x+1\right)\left[x^2-x+1-9x+15\right]=\left(x+1\right)\left(x^2-10x+16\right)\)
\(=\left(x+1\right)\left[x\left(x-2\right)-8\left(x-2\right)\right]\)\(\left(x+1\right)\left(x-2\right)\left(x-8\right)\)
3) \(x^3-6x^2-x+30\)
\(=x^3-5x^2-x^2+5x-6x+30\)
\(=x^2\left(x-5\right)-x\left(x-5\right)-6\left(x-5\right)\)
\(=\left(x-5\right)\left(x^2-x-1\right)\)
4) \(2x^3-x^2+5x+3=\left(2x^3+x^2\right)-\left(2x^2+x\right)+\left(6x+3\right)\)
\(=x^2\left(2x+1\right)-x\left(2x+1\right)+3\left(2x+1\right)\)
\(=\left(2x+1\right)\left(x^2-x+3\right)\)
5) \(27x^3-27x^2+18x-4=\left(27x^3-1\right)-\left(27x^2-18x+3\right)\)
\(=\left(3x-1\right)\left(9x^2+3x+1\right)-3\left(9x^2-6x+1\right)\)
\(=\left(3x-1\right)\left(9x^2+3x+1\right)-3\left(3x-1\right)^2\)
\(=\left(3x-1\right)\left(9x^2+3x+1-9x+3\right)=\left(3x-1\right)\left(9x^2-6x+4\right)\)
gửi phần này trước còn lại làm sau !!! tk mk nka !!!
6) \(\left(x+y\right)^2-\left(x+y\right)-12\)\(=\left(x+y\right)^2-2\cdot\frac{1}{2}\left(x+y\right)+\frac{1}{4}-\frac{49}{4}\)
\(=\left(x+y-\frac{1}{2}\right)^2-\left(\frac{7}{2}\right)^2\)\(=\left(x+y-\frac{1}{2}-\frac{7}{2}\right)\left(x+y-\frac{1}{2}+\frac{7}{2}\right)\)
\(=\left(x-4\right)\left(x+3\right)\)
7) \(\left(x+2\right)\left(x+5\right)\left(x+3\right)\left(x+4\right)-24\) (NHÂN x + 2 vs x + 5 và x + 3 vs x + 4 )
\(=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\)
ĐẶT \(x^2+7x+11=y\) ta được :
\(\left(y+1\right)\left(y-1\right)-24=y^2-1-24\)
\(=y^2-25=\left(y-5\right)\left(y+5\right)\)
8) \(4x^4-32x^2+1=4x^4+4x^2+1-36x^2\)
\(=\left(2x^2+1\right)^2-\left(6x\right)^2\)\(=\left(2x^2-6x+1\right)\left(2x^2+6x+1\right)\)
9) sai đề rùi bạn ơi ! đề đúng nè
\(3\left(x^4+x^2+1\right)-\left(x^2+x+1\right)^2\)
Ta thấy :
\(x^4+x^2+1=\left(x^4+2x^2+1\right)-x^2\)\(=\left(x^2+1\right)^2-x^2=\left(x^2+x+1\right)\left(x^2-x+1\right)\)
Thay vào biểu thức bài cho ta được :
\(3\left(x^2-x+1\right)\left(x^2+x+1\right)-\left(x^2+x+1\right)^2\)
\(=\left(x^2+x+1\right)\left(3x^2-3x+3-x^2-x-1\right)\)
\(=\left(x^2+x+1\right)\left(2x^2-4x+2\right)\)
\(=2\left(x^2+x+1\right)\left(x-1\right)^2\)
bài ở trên câu 3 : kết luận là \(\left(x-3\right)\left(x^2-x-6\right)\)bạn sửa lại giúp mk nka !!! Th@nk !!! Tk Mk vs
Bài 1 : Tìm các số tự nhiên \(x\) thoả mãn : \(2^x+3^x=35\)
Bài 2 : Tìm \(x;y\inℤ^+\) thoả mãn : \(x!+y!=\left(x+y\right)!\)
Bài 3 : Chứng minh rằng phương trình sau không có nghiệm nguyên :
\(x^{17}+y^{17}=19^{17}\)
Bài 1: Bài này số nhỏ nên chỉ cần chặn miền giá trị của \(x\) rồi xét các trường hợp thôi nhé. Ta thấy \(3^x< 35\Leftrightarrow x\le3\). Nếu \(x=0\) thì \(VT=2\), vô lí. Nếu \(x=1\) thì \(VT=5\), cũng vô lí. Nếu \(x=2\) thì \(VT=13\), vẫn vô lí. Nếu \(x=3\) thì \(VT=35\), thỏa mãn. Vậy, \(x=3\).
Bài 2: Nếu \(x=0\) thì pt đã cho trở thành \(0!+y!=y!\Leftrightarrow0=1\), vô lí,
Nếu \(x=y\) thì pt trở thành \(2x!=\left(2x\right)!\) \(\Rightarrow\left(x+1\right)\left(x+2\right)...\left(2x\right)=2\) \(\Leftrightarrow x=1\Rightarrow y=1\)
Nếu \(x\ne y\) thì không mất tính tổng quát, giả sử \(1< y< x\) thì \(x!+y!< 2x!\le\left(x+1\right)x!=\left(x+1\right)!< \left(x+y\right)!\) nên pt đã cho không có nghiệm trong trường hợp này.
Như vậy, \(x=y=1\)
Bài 3: Bổ sung đề là pt không có nghiệm nguyên dương nhé, chứ nếu nghiệm nguyên thì rõ ràng \(\left(x,y\right)=\left(0,19\right)\) là một nghiệm cũa pt đã cho rồi.
Giả sử pt đã cho có nghiệm nguyên dương \(\left(x,y\right)\)
Khi đó \(x,y< 19\). Không mất tính tổng quát ta có thể giả sử \(1< y\le x< 19\). Khi ấy \(x^{17}+y^{17}=19^{17}\ge\left(x+1\right)^{17}=x^{17}+17x^{16}+...>x^{17}+17x^{16}\), suy ra \(y^{17}>17x^{16}\ge17y^{16}\) \(\Rightarrow y>17\). Từ đó, ta thu được \(17< y\le x< 19\) nên \(x=y=18\). Thử lại thấy không thỏa mãn.
Vậy pt đã cho không có nghiệm nguyên dương.
Chị độc giải sau khi em biết làm thôi à.
Gọi x1, x2 là nghiệm của phương trình |46x + 49| = |19x + 17|. Tìm |x1 − x2|.
\(\left|46x+49\right|=\left|19x+17\right|\)
\(\Rightarrow\orbr{\begin{cases}46x+49=19x+17\\46x+49=-19x-17\end{cases}\Rightarrow\orbr{\begin{cases}x=-\frac{32}{27}\\x=-\frac{66}{65}\end{cases}}}\)
\(\Rightarrow\left|x_1-x_2\right|=\left|-\frac{32}{27}-\frac{66}{65}\right|=....\)
Phân tích các đa thức sau thành nhân tử:
1) x3 - 7x + 6
2) x3 - 9x2 + 6x + 16
3) x3 - 6x2 - x + 30
4) 2x3 - x2 + 5x + 3
5) 27x3 - 27x2 + 18x - 4
6) x2 + 2xy + y2 - x - y - 12
7) (x + 2)(x +3)(x + 4)(x + 5) - 24
8) 4x4 - 32x2 + 1
9) 3(x4 + x2 + 1) - (x2 + x + 1)2
10) 64x4 + y4
11) a6 + a4 + a2b2 + b4 - b6
12) x3 + 3xy + y3 - 1
13) 4x4 + 4x3 + 5x2 + 2x + 1
14) x8 + x + 1
15) x8 + 3x4 + 4
16) 3x2 + 22xy + 11x + 37y + 7y2 +10
17) x4 - 8x + 63
a,\(x^3-7x+6\)
\(=x^3-2x^2+2x^2-4x-3x+6\)
\(=\left(x^3-2x^2\right)+\left(2x^2-4x\right)-\left(3x-6\right)\)
\(=x^2.\left(x-2\right)+2x.\left(x-2\right)-3.\left(x-2\right)\)
\(=\left(x-2\right).\left(x^2+2x-3\right)\)
\(=\left(x-2\right).\left(x^2-x+3x-3\right)\)
\(=\left(x-2\right).\left[\left(x^2-x\right)+\left(3x-3\right)\right]\)
\(=\left(x-2\right).\left[x.\left(x-1\right)+3.\left(x-1\right)\right]\)
\(=\left(x-2\right).\left(x-1\right).\left(x+3\right)\)
b,\(x^3-9x^2+6x+16\)
\(=x^3-8x^2-x^2+8x-2x+16\)
\(=\left(x^3-8x^2\right)-\left(x^2-8x\right)-\left(2x-16\right)\)
\(=x^2.\left(x-8\right)-x.\left(x-8\right)-2.\left(x-8\right)\)
\(=\left(x-8\right).\left(x^2-x-2\right)\)
\(=\left(x-8\right).\left(x^2+x-2x-2\right)\)
\(=\left(x-8\right).\left[\left(x^2+x\right)-\left(2x+2\right)\right]\)
\(=\left(x-8\right).\left[x.\left(x+1\right)-2.\left(x+1\right)\right]\)
\(=\left(x-8\right).\left(x+1\right).\left(x-2\right)\)
c,\(x^3-6x^2-x+30\)
\(=x^3-5x^2-x^2+5x-6x+30\)
\(=\left(x^3-5x^2\right)-\left(x^2-5x\right)-\left(6x-30\right)\)
\(=x^2.\left(x-5\right)-x.\left(x-5\right)-6.\left(x-5\right)\)
\(=\left(x-5\right).\left(x^2-x-6\right)\)
\(=\left(x-5\right).\left(x^2+2x-3x-6\right)\)
\(=\left(x-5\right).\left[\left(x^2+2x\right)-\left(3x+6\right)\right]\)
\(=\left(x-5\right).\left[x.\left(x+2\right)-3.\left(x+2\right)\right]\)
\(=\left(x-5\right).\left(x+2\right).\left(x-3\right)\)
Chúc bạn học tốt!!!
d,\(2x^3-x^2+5x+3\)
\(=2x^3+x^2-2x^2-x+6x+3\)
\(=\left(2x^3+x^2\right)-\left(2x^2+x\right)+\left(6x+3\right)\)
\(=x^2.\left(2x+1\right)-x.\left(2x+1\right)+3.\left(2x+1\right)\)
\(=\left(2x+1\right).\left(x^2-x+3\right)\)
e, \(27x^3-27x^2+18x-4\)
\(=27x^3-9x^2-18x^2+6x+12x-4\)
\(=\left(27x^2-9x^2\right)-\left(18x^2-6x\right)+\left(12x-4\right)\)
\(=9x^2.\left(3x-1\right)-6x.\left(3x-1\right)+4.\left(3x-1\right)\)
\(=\left(3x-1\right).\left(9x^2-6x+4\right)\)
Chúc bạn học tốt!!!
7, \(\left(x+2\right).\left(x+3\right).\left(x+4\right).\left(x+5\right)-24\)
\(=\left[\left(x+2\right).\left(x+5\right)\right].\left[\left(x+3\right).\left(x+4\right)\right]-24\)
\(=\left(x^2+5x+2x+10\right).\left(x^2+4x+3x+12\right)-24\)
\(=\left(x^2+7x+10\right).\left(x^2+7x+12\right)-24\)(1)
Đặt \(t=x^2+7x+10\Rightarrow t+2=x^2+7x+12\)
\(\Rightarrow\left(1\right)=t.\left(t+2\right)-24\)
\(=t^2+2t-24=t^2-4t+6t-24\)
\(=\left(t^2-4t\right)+\left(6t-24\right)=t.\left(t-4\right)+6.\left(t-4\right)\)
\(=\left(t-4\right).\left(t+6\right)\) (2)
Vì \(t=x^2+7x+10\) nên:
(2) \(=\left(x^2+7x+10-4\right).\left(x^2+7x+10+6\right)\)
\(=\left(x^2+7x+6\right).\left(x^2+7x+16\right)\)
\(=\left(x^2+x+6x+6\right).\left(x^2+7x+16\right)\)
\(=\left[\left(x^2+x\right)+\left(6x+6\right)\right].\left(x^2+7x+16\right)\)
\(=\left[x.\left(x+1\right)+6.\left(x+1\right)\right].\left(x^2+7x+16\right)\)
\(=\left(x+1\right).\left(x+6\right).\left(x^2+7x+16\right)\)
Chúc bạn học tốt!!!
Gọi x1, x2 là nghiệm của phương trình x^2+2009x+1=0,
x3,x4 là nghiệm của phương trình x^2+2010x+1=0.
Tính giá trị biểu thức (x1+x3)(x2+x3)(x1-x4)(x2-x4)
Cho phương trình: x 4 - 13 x 2 + m = 0 . Tìm các giá trị của m để phương trình: Có 2 nghiệm phân biệt

Phương trình (1) có hai nghiệm phân biệt khi phương trình (2) có nghiệm kép hoặc có 1 nghiệm dương và một nghiệm âm.
Phương trình (2) có một nghiệm số kép khi và chỉ khi Δ = 169 - 4m = 0
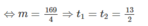
Phương trình (2) có một nghiệm số dương và một nghiệm số âm khi
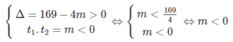
Vậy với m = 169/4 hoặc m < 0 thì phương trình (1) có 2 nghiệm phân biệt.
Giải phương trình nghiệm nguyên \(x^2+4y^2+28=17\left(x^4+y^4+14y^2+49\right)\)
mày bị ngáo ak. đã xấu còn bị điên. đã bị điên cò học dốt
y^2+7=z
\(\Leftrightarrow x^2+4z=17\left(x^4+z^2\right)\)Hiển nhiên \(VP\ge VT\) đẳng thức chỉ xẩy ra khi x=z=0
với z=0=> y^2+7=0 vô nghiệm
KL vô nghiệm nguyên