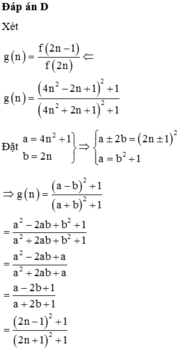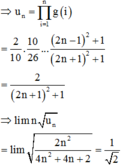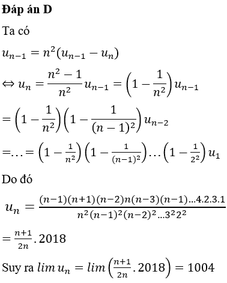Lim Un = 1 + 2 + 3 +...+ n/ n2 + 1

Những câu hỏi liên quan
Đặt
f
(
n
)
(
n
2
+
n
+
1
)
2
+
1
.
Xét dãy số
(
u
n
)
sao cho
u
n
f
(
1...
Đọc tiếp
Đặt f ( n ) = ( n 2 + n + 1 ) 2 + 1 . Xét dãy số ( u n ) sao cho u n = f ( 1 ) . f ( 3 ) . f ( 5 ) . . . f ( 2 n - 1 ) f ( 2 ) . f ( 4 ) . f ( 6 ) . . . f ( 2 n ) . Tính lim n u n
A. l i m n u n = 2
B. l i m n u n = 1 3
C. l i m n u n = 3
D. l i m n u n = 1 2
Cho dãy số
u
1
2018
u
n
-
1
n
2
(...
Đọc tiếp
Cho dãy số u 1 = 2018 u n - 1 = n 2 ( u n - 1 - u n ) ( n ∈ N * ) . Tính lim u n
A. 2018
B. 2017
C. 1004
D. 1003
Cho dãy số
(
u
n
)
với
u
n
n
2
+
1
-
n
. Tính lim
u
n
A. 0 B.1 C.
-
∞
D.
+
∞
Đọc tiếp
Cho dãy số ( u n ) với u n = n 2 + 1 - n . Tính lim u n
A. 0
B.1
C. - ∞
D. + ∞
Ta có: u n = n 2 + 1 − n = n 2 + 1 − n n 2 + 1 + n n 2 + 1 + n = 1 n 1 + 1 n 2 + 1 = 1 n . 1 1 + 1 n 2 + 1
Vì lim 1 n = 0 , lim 1 1 + 1 n 2 + 1 = 1 2 nên lim u n = 0 .
Chọn đáp án A.
Đúng 0
Bình luận (0)
Đặt f(n)
n
2
+
n
+
1
2
+
1
Xét dãy số (
u
n
)sao cho
u
n
f
(
1
)
.
f...
Đọc tiếp
Đặt f(n)= n 2 + n + 1 2 + 1
Xét dãy số ( u n )sao cho
u n = f ( 1 ) . f ( 3 ) . f ( 5 ) . . . f ( 2 n - 1 ) f ( 2 ) . f ( 4 ) . f ( 6 ) . . . f ( 2 n ) .
Tính lim n u n .
![]()
![]()
![]()
![]()
Cho dãy số
(
u
n
)
với
u
n
n
-
1
2
n
+
2
n
4
+
n
2
-...
Đọc tiếp
Cho dãy số ( u n ) với u n = n - 1 2 n + 2 n 4 + n 2 - 1 . Tính l i m u n là:
A. - 1
B. 0
C. 1
D. 2
Ta có:
lim u n = lim n − 1 2 n + 2 n 4 + n 2 − 1 = lim n − 1 2 2 n + 2 n 4 + n 2 − 1 = lim u n = lim n − 1 2 n + 2 n 4 + n 2 − 1 = lim 2 n − 2 n 2 − 2 n 3 + 2 n 4 1 + 1 n 2 − 1 n 4 = 0.
Chọn đáp án B
Đúng 0
Bình luận (0)
Cho dãy số
u
n
với
u
n
n
-
1
2
n
+
2
n
4
+
n
2
-
1
. Chọn kết quả đúng của
l
i
m...
Đọc tiếp
Cho dãy số u n với u n = n - 1 2 n + 2 n 4 + n 2 - 1 . Chọn kết quả đúng của l i m u n là:
A. - ∞
B. 0
C. 1
D. + ∞
Đáp án là B
Ta có: l i m u n = l i m n - 1 2 n + 2 n 4 + n 2 - 1
=
l
i
m
n
-
1
2
2
n
+
2
n
4
+
n
2
-
1
=
l
i
m
2
n
3
-
2
n
2
-
2
n
+
2
n
4
+
n
2
-
1
= l i m 2 n - 2 n 2 - 2 n 3 + 2 n 4 1 + 1 n 2 - 1 n 4 = 0
Đúng 0
Bình luận (0)
Đặt
f
n
n
2
+
n
+
1
2
+
1.
Xét dãy số
u
n
sao cho
u
n
f
1
....
Đọc tiếp
Đặt f n = n 2 + n + 1 2 + 1. Xét dãy số u n sao cho u n = f 1 . f 3 . f 5 ... f 2 n − 1 f 2 . f 4 . f 6 ... f 2 n . lim n u n .
A. lim n u n = 2
B. lim n u n = 1 3
C. lim n u n = 3
D. lim n u n 1 2
Đáp án là D.
Ta có
f n = n 2 + 1 + n 2 + 1 = n 2 + 1 2 + 2 n . n 2 + 1 + n 2 + 1 = n 2 + 1 n 2 + 1 + 2 n + 1
= n 2 + 1 n + 1 2 + 1
Do đó: f 2 n − 1 f 2 n = 2 n − 1 2 + 1 2 n 2 + 1 2 n 2 + 1 2 n + 1 2 + 1 = 2 n − 1 2 + 1 2 n + 1 2 + 1
Suy ra
u n = f 1 . f 3 . f 5 ... f 2 n − 1 f 2 . f 4 . f 6 ... f 2 n = f 1 f 2 ⋅ f 3 f 4 ⋅ f 5 f 6 ⋅ ⋅ ⋅ f 2 n − 1 f 2 n
= 1 2 + 1 3 2 + 1 ⋅ 3 2 + 1 5 2 + 1 ⋅ 5 2 + 1 7 2 + 1 ⋅ ⋅ ⋅ 2 n − 1 2 + 1 2 n + 1 2 + 1 = 2 2 n + 1 2 + 1 = 1 2 n 2 + 2 n + 1
⇒ n u n = n . 1 2 n 2 + 2 n + 1
⇒ lim n u n = 1 2
Đúng 0
Bình luận (0)
Cho dãy số
(
u
n
)
với
u
n
n
+
n
2
+
1
n
.
3
n
. Tính
l
i
m
u...
Đọc tiếp
Cho dãy số ( u n ) với u n = n + n 2 + 1 n . 3 n . Tính l i m u n
A. 1 3
B. + ∞
C. 1 4
D. 0
Ta có: u n = n + n 2 + 1 n .3 n = n + n 2 + 1 n n .3 n n = 1 + 1 + 1 n 2 3 n = 1 3 n 1 + 1 + 1 n 2
Vì lim 1 n 2 = 0 nên lim 1 + 1 + 1 n n = 2 và lim 1 3 n = 0.
Do đó lim u n = 0
Chọn đáp án D
Đúng 0
Bình luận (0)
Tính lim
u
n
với
u
n
2
n
3
-
3
n
2
+
n
+
5
n
3
-
n
2
+
7
A. -3 B. 1...
Đọc tiếp
Tính lim u n với u n = 2 n 3 - 3 n 2 + n + 5 n 3 - n 2 + 7
A. -3
B. 1
C. 2
D. 0
Chia cả tử và mẫu của phân thức cho n 3 ( n 3 là lũy thừa bậc cao nhất của n trong phân thức), ta được:
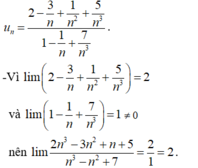
Chọn C.
Đúng 0
Bình luận (0)