x/15 = -1/3
các bạn và thầy cô giúp em với ạ !
Thầy cô các anh chị và các bạn giúp em với ạ, em cần gấp ạ

Câu 1 Đề sai bạn
VD a = 5 ; b = 4
=> a2 - ab + b = 52 - 5.4 + 4 = 9 \(⋮\)9
nhưng a ; b \(⋮̸\)3
Nhờ thầy cô và các bạn giúp đỡ em với ạ
Tính Nhanh \(A=\left(1+12\right).\left(1+13\right).\left(1+14\right).\left(1+15\right).\left(1+16\right).\)
P/s: Em nhờ quý thầy cô giáo và các bạn yêu toán gợi ý và giúp đỡ với ạ!
Em cám ơn nhiều ạ!
\(A=1.\left(12+13+14+15+16\right)\)
\(A=1.70\)
\(A=70\)
\(A=\left(1+12\right).\left(1+13\right).\left(1+14\right).\left(1+15\right).\left(1+16\right)\\ =1.\left(12+13+14+15+16\right)\\ =1.70\\ =70\)
Nhờ thầy cô và các bạn giúp đỡ với ạ. Em cám ơn nhiều ạ!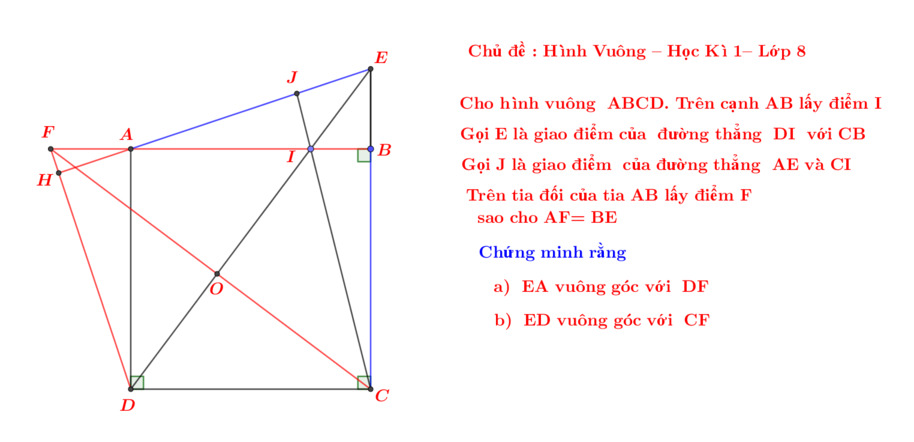
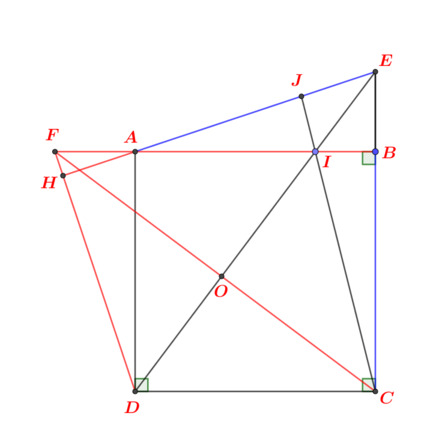
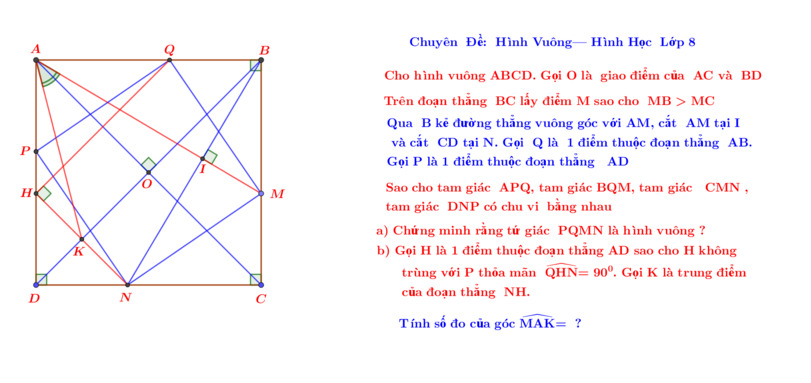
Em xin phép nhờ quý thầy cô và các bạn giúp đỡ với ạ, em cám ơn nhiều ạ
-Để mình suy nghĩ ngồi làm cho bạn nhé.
-Vì bài dài quá nên mình nói tóm tắt:
a) -Bạn chứng minh △ABM = △BCN (g-c-g) do có \(AB=BC\) , \(\widehat{BCN}=\widehat{ABM}=90^0\),\(\widehat{NBC}=\widehat{MAB}\) (bạn tự chứng minh).
-Suy ra: \(BM=CN\) .
-Suy ra 2 điều:
+\(QM^2-BQ^2=MN^2-MC^2\)
+\(QM+BQ=MN+MC\) (1)
\(QM^2-BQ^2=MN^2-MC^2\)
\(\Rightarrow\left(QM-BQ\right)\left(QM+BQ\right)=\left(MN-MC\right)\left(MN+MC\right)\)
\(\Rightarrow QM-BQ=MN-MC\) (2)
-Từ (1),(2) suy ra \(QM=MN\) nên △BMQ=△CNM (ch-cgv).
\(\Rightarrow\) MQ vuông góc với MN (bạn tự c/m).
\(QM=MN\) nên \(BQ=MC\) nên \(AQ=BM\Rightarrow PQ^2-AP^2=QM^2-BQ^2;QM+BQ=PQ+AP\)
Nên \(PQ=QM;\Delta APQ=\Delta BQM\) nên PQ⊥QM ; AP=BQ nên PQ=AQ
-Từ PQ=AQ bạn tự c/m PN=PQ (theo sườn mình đã cho) rồi sau đó c/m tam giác APQ=tam giác DNP rồi từ đó suy ra PQ vuông góc PN
.......
Nhờ thầy cô và các bạn trong nhóm giúp đỡ em với ạ!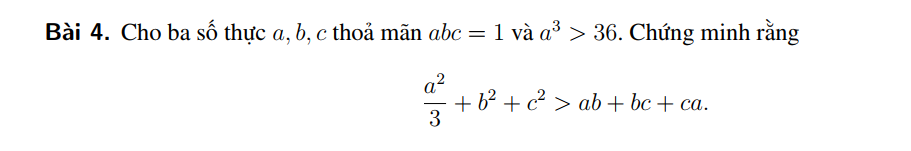
Từ GT \(\Leftrightarrow a>0;bc>0\)
\(BĐT\Leftrightarrow\dfrac{a^2}{3}+\left(b+c\right)^2-3bc-a\left(b+c\right)\ge0\\ \Leftrightarrow\dfrac{1}{3}+\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}-\dfrac{3}{a^2}\ge0\)
Vì \(a^3>36\) nên
\(\dfrac{1}{3}+\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}-\dfrac{3}{a^2}\\ >\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}+\dfrac{1}{4}=\left(\dfrac{b+c}{a}-\dfrac{1}{2}\right)^2\ge0\)
Có tồn tại hay không các số nguyên dương \(x;y;n\) với \(n>1\) thỏa mãn điều kiện \(\left(x;n+1\right)=1\) và \(x^n+1=y^{n+1}\) ?
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn giúp đỡ em tham khảo với ạ, em cám ơn nhiều ạ!
Em xin phép nhờ thầy cô và các bạn giúp đỡ với ạ, em cám ơn nhiều
Dạ thầy cô và các bạn giúp em cách làm câu 6a với ạ.
Em cảm ơn
\(y'=\left(m+3\right)x^2-4x+m\)
Hàm nghịch biến trên R khi và chỉ khi \(y'\le0\) ; \(\forall x\in R\)
- Với \(m=-3\) ko thỏa mãn
- Với \(m\ne-3\) bài toán thỏa mãn khi:
\(\left\{{}\begin{matrix}m+3< 0\\\Delta'=4-m\left(m+3\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -3\\\left[{}\begin{matrix}m\ge1\\m\le-4\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow m\le-4\)