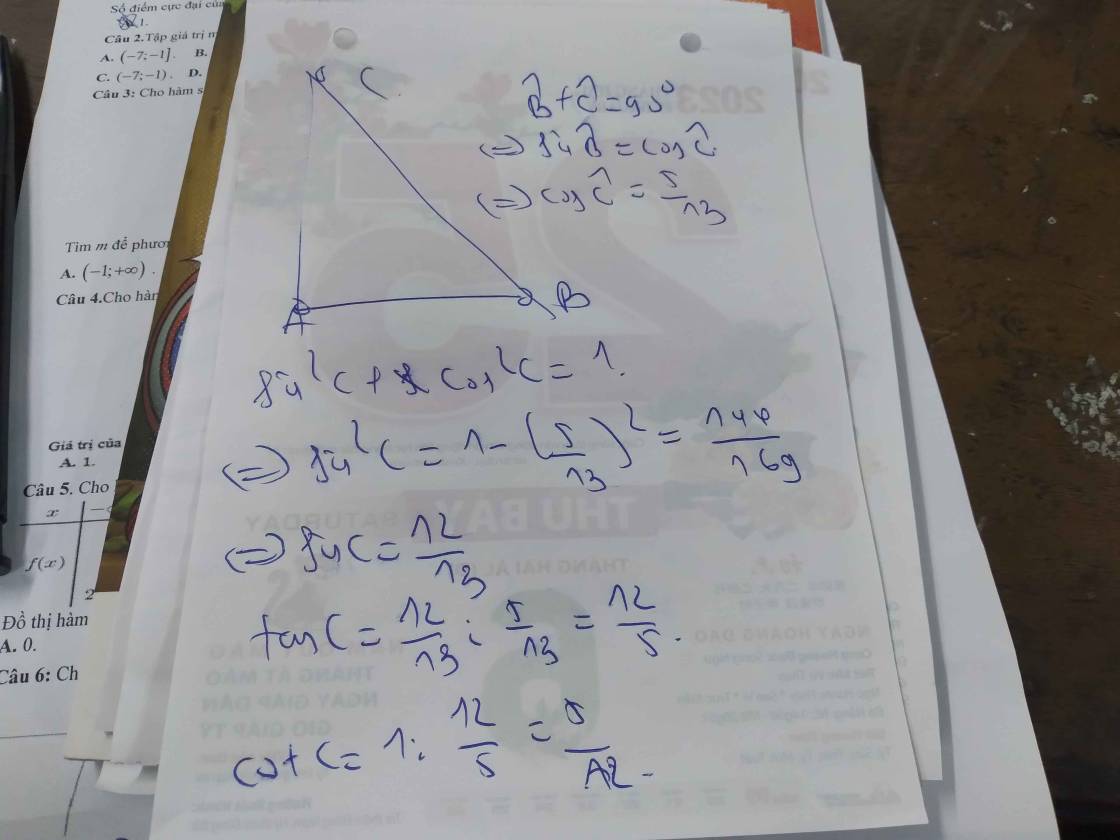
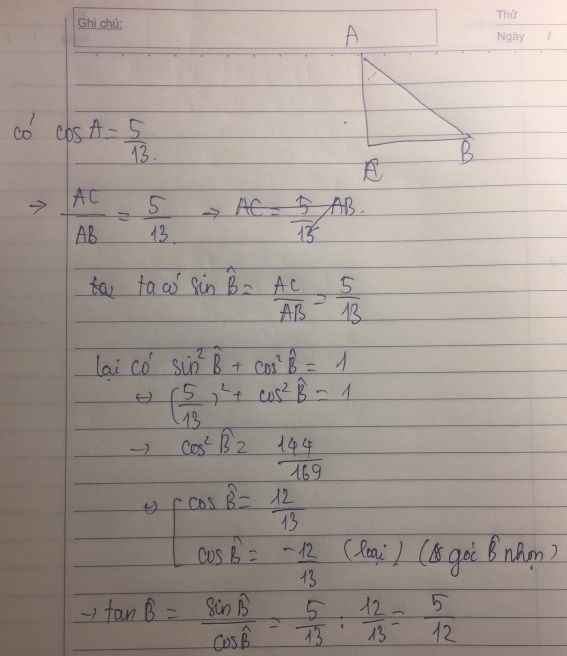cho tam giac ABC vuông tại C. Biết cosA=5/13. Tính tỉ số lượng gíac góc B

Những câu hỏi liên quan
* Cho tam giác ABC vuông tại C. Biết cosA=\(\dfrac{5}{13}\). Tính tan B
\(\sin\widehat{A}=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\)
\(\cot\widehat{A}=\dfrac{5}{13}:\dfrac{12}{13}=\dfrac{5}{12}\)
\(\tan\widehat{B}=\dfrac{5}{12}\)
Đúng 2
Bình luận (0)
Cho tam giac ABC vuông tại B=0,6.tính các tỉ số lượng giác của góc c
Cho tam giác ABC vuông tại A và sinB = \(\dfrac{5}{13}\).Tính các tỉ số lượng giác của góc C
Có:
\(cosC=sinB=\dfrac{5}{13}\)
\(cosB=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\\ \Rightarrow sinC=\dfrac{12}{13}\)
\(tgC=\dfrac{sinC}{cosC}=\dfrac{\dfrac{12}{13}}{\dfrac{5}{13}}=\dfrac{12}{5}\)
\(\Rightarrow cotgC=\dfrac{5}{12}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại C.biết cosA=5/13 và BC=10cm.Hãy tính độ dài các cạnh góc vuông
Lời giải:
Ta có:
$\frac{5}{13}=\cos A=\frac{AC}{AB}$
$\Rightarrow AB=\frac{13}{5}AC$
Áp dụng định lý Pitago:
$AC^2+BC^2=AB^2$
$\Leftrightarrow AC^2+10^2=(\frac{13}{5}AC)^2$
$\Leftrightarrow 100=\frac{144}{25}AC^2$
$\Leftrightarrow AC^2=\frac{625}{36}$
$\Rightarrow AC=\frac{25}{6}$ (cm)
Vậy......
Đúng 1
Bình luận (0)
CHO TAM GIÁC ABC VUÔNG TẠI A,CÓ ĐƯỜNG CAO AH. TÍNH CÁC TỈ SỐ LƯỢNG GIÁC CỦA GÓC C, TỪ ĐÓ SUY RA CÁC TỈ SỐ LƯỢNG GIÁC GÓC B,NẾU BIẾT RẰNG
a) AC=13, CH=15
b)BH=3cm, CH=4
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=21\\AC^2=28\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{21}\left(cm\right)\\AC=2\sqrt{7}\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AC}{BC}=\dfrac{2\sqrt{7}}{7}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{\sqrt{21}}{7}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{AC}{AB}=\dfrac{2\sqrt{7}}{\sqrt{21}}=\dfrac{2\sqrt{3}}{3}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{AB}{AC}=\dfrac{\sqrt{21}}{2\sqrt{7}}=\dfrac{\sqrt{3}}{2}\)
Đúng 0
Bình luận (0)
sin,cos,tan..nhé
cho tam giac abc vuông tại a . biết cosb=0,tám
hãy tính các tỉ số lượng giác của góc c
cosB=0,8=4/5 => BA=4 , BC=5
Áp dụng định lý Pytago trong tam giác vuông ABC, có:
AC2=BC2-BA2
(=) AC2=52-42=9
(=) AC=3
Ta có:
sinC=BA/BC=4/5
cosC=AC/BC=3/5
tanC=BA/AC=4/3
cotC=AC/BA=3/4
Đúng 0
Bình luận (0)
\(sin^2B+cos^2B=1\Leftrightarrow sin^2B-1-\left(0,8\right)^2=0.36.\Leftrightarrow sinB=0,6.\\\)
\(tanB=\frac{sinB}{cosB}=\frac{0,6}{0,8}=\frac{3}{4}\)
\(cotB=\frac{1}{tanB}=\frac{1}{\frac{3}{4}}=\frac{4}{3}.\)
Đúng 0
Bình luận (0)
\(sinC=cosB=0,8\)
\(cosC=sinB=0,6\)
\(tanC=cotB=\frac{4}{3}\)
\(cotC=tanB=\frac{3}{4}.\)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A biết góc B =56 độ tính tỉ số lượng giác của góc B từ đó suy ra các tỉ số lượng giá của góc C
Xét ΔABC vuông tại A có
\(sinB=sin56\simeq0,83\)
\(cosB=cos56\simeq0,56\)
\(tanB=tan56\simeq1,48\)
\(cotB=cot56\simeq0,67\)
Xét ΔABC vuông tại A có
\(cosC=sinB\simeq0,83\)
\(sinC=cosB\simeq-0,56\)
\(cotC=tanB=tan56\simeq1,48\)
\(tanC=cotB\simeq0,67\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại C có sinA=3/5 .không tính số đo góc A.Hãy tính cosA,tanA,cotA
\(\sin^2\widehat{A}+\cos^2\widehat{A}=1\Leftrightarrow\cos^2\widehat{A}=1-\left(\dfrac{3}{5}\right)^2=1-\dfrac{9}{25}=\dfrac{16}{25}\\ \Leftrightarrow\cos\widehat{A}=\dfrac{4}{5}\\ \tan\widehat{A}=\dfrac{\sin\widehat{A}}{\cos\widehat{A}}=\dfrac{3}{4}\\ \Rightarrow\cot\widehat{A}=\dfrac{1}{\tan\widehat{A}}=\dfrac{4}{3}\)
Đúng 3
Bình luận (0)
Cho tam giác ABC vuông tại C có sinA=3/5 .không tính số đo góc A.Hãy tính cosA,tanA,cotA.