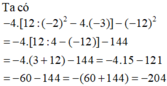122+(-22)+(-1)+25.4

Những câu hỏi liên quan
A= -5^22{-222[-122-(100-5^22)+2022]}
\(A=-5^{22}\left\{-222\left[-122-\left(100-5^{22}\right)+2022\right]\right\}\)
\(A=-5^{22}\left\{-222\left[1900-\left(100-5^{22}\right)\right]\right\}\)
\(A=-5^{22}\left[-222\left(1900-100+5^{22}\right)\right]\)
\(A=-5^{22}\left[-222\left(1800+5^{22}\right)\right]\)
\(A=-5^{22}\left(-399600-222\cdot5^{22}\right)\)
\(A=399600\cdot5^{22}+222\cdot5^{44}\)
Đúng 1
Bình luận (0)
5^22-{222-[122-(100+5^22)+2022]} bằng bao nhiêu vậy ạ
Lời giải:
$=5^{22}-22+[122-(100+5^{22})+2022]$
$=5^{22}-22+122-100-5^{22}+2022$
$=(5^{22}-5^{22})+(-22+122-100)+2022$
$=0+0+2022=2022$
Đúng 1
Bình luận (0)
14 + |-122| -22-(-86)
14+|-122| -22-(-86)
= 14+122-22+86
=136-22+86
=200
\(14+\left|-122\right|-22-\left(-86\right)\)
\(=14+122-22+86\)
\(=\left(14+86\right)+\left(122-22\right)\)
\(=100+100=200\)
~ Học tốt@@
# Chiyuki Fujito
Xem thêm câu trả lời
122+22=
Tổng là:
122 + 22 = 144
Đáp số:144
Chúc giáng sinh vui vẻ
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
(3.x+1)^2=25.4. tìm x
`(3x+1)^2=25.4`
<=> `(3x+1)^2=10^2`
<=> `3x+1=10` hoặc `3x+1=-10`
<=> `x=3` hoặc `x=-11/3`
Đúng 1
Bình luận (0)
\(\left(3x+1\right)^2=25.4\\ < =>\sqrt{\left(3x+1\right)^2}=\sqrt{100}< =>3x+1=10\\ < =>3x=9\\ < =>x=3\\\)
Đúng 0
Bình luận (0)
Ta có : (3x + 1)2 = 25 . 4
=> (3x + 1)2 = 100
=> (3x + 1) = 102
=> 3x + 1 = 10
=> x = 3
Đúng 0
Bình luận (0)
Tính -4.[12:
-
2
2
-4.(-3)-
-
12
2
] ta được kết quả là A. −144 B. 144 C. −204 D. 204
Đọc tiếp
Tính -4.[12: - 2 2 -4.(-3)- - 12 2 ] ta được kết quả là
A. −144
B. 144
C. −204
D. 204
tinh nhanh:
1+1+1+1+11+11+25.4+10+5+1
1+1+1+1+11+11+25.4+10+5+1
=4+11.2+25.4+10+6
=4+6+10+100+121
=10+10+221
=20+221
=241
k mình nha!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
The product of the whole numbers from 1 to 122 is divisible by 22n. Find the greatest possible value of the whole number n.
\(22^n=2^n.11^n\)
\(122!=1.2...11...22...33...44...55...66...77...88...99...110...121\)
\(=11^{11}.A\)
\(\Rightarrow n_{max}=11\)
Đúng 0
Bình luận (0)
A-5^{22}-left{-222-left[-122-left(100-5^{22}right)+2022right]right}
B1+dfrac{1}{2}left(1+2right)+dfrac{1}{3}left(1+2+3right)+...+dfrac{1}{20}left(1+2+3+...+20right)
Cdfrac{5.4^6.9^4-3^9.left(-8right)^4}{4.2^{13}.3^8+2.8^4.left(-27right)^3}
Đọc tiếp
\(A=-5^{22}-\left\{-222-\left[-122-\left(100-5^{22}\right)+2022\right]\right\}\)
\(B=1+\dfrac{1}{2}\left(1+2\right)+\dfrac{1}{3}\left(1+2+3\right)+...+\dfrac{1}{20}\left(1+2+3+...+20\right)\)
\(C=\dfrac{5.4^6.9^4-3^9.\left(-8\right)^4}{4.2^{13}.3^8+2.8^4.\left(-27\right)^3}\)
A = - 522 - { - 222 - [ - 122 - (100 - 522) + 2022] }
A = - 522 - { -222 - [- 122 - 100 + 522 ] + 2022}
A = - 522 - { -222 - { - 222 + 522 } + 2022}
A = - 522 - {- 222 + 222 - 522 + 2022}
A = -522 + 522 - 2022
A = - 2022
Đúng 1
Bình luận (0)
B = 1 + \(\dfrac{1}{2}\)(1 + 2) + \(\dfrac{1}{3}\).(1 + 2 + 3) + ... + \(\dfrac{1}{20}\).(1 + 2+ 3 + ... + 20)
B = 1+\(\dfrac{1}{2}\)\(\times\)(1+2)\(\times\)[(2-1):1+1]:2+ ... + \(\dfrac{1}{20}\)\(\times\) (20 + 1)\(\times\)[(20-1):1+1]:2
B = 1 + \(\dfrac{1}{2}\) \(\times\) 3 \(\times\) 2:2 + \(\dfrac{1}{3}\) \(\times\)4 \(\times\) 3 : 2+....+ \(\dfrac{1}{20}\) \(\times\)21 \(\times\) 20 : 2
B = 1 + \(\dfrac{3}{2}\) + \(\dfrac{4}{2}\) + ....+ \(\dfrac{21}{2}\)
B = \(\dfrac{2+3+4+...+21}{2}\)
B = \(\dfrac{\left(21+2\right)\left[\left(21-2\right):1+1\right]:2}{2}\)
B = \(\dfrac{23\times20:2}{2}\)
B = \(\dfrac{23\times10}{2}\)
B = 23
Đúng 0
Bình luận (0)