Cho bz−cy
a
=cx−az
b
=ay−bx
c . Chứng minh rằng x
a
= y
b
= z
c

Những câu hỏi liên quan
Biết rằng:
b
z
-
c
y
a
c
x
-
a
z
b
a
y
-
b
x
c...
Đọc tiếp
Biết rằng: b z - c y a = c x - a z b = a y - b x c Hãy chứng minh x : y : z = a : b : c
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
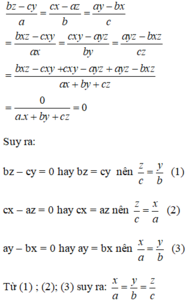
Hay x : y : z = a : b : c
Đúng 0
Bình luận (0)
bz−cya = cx−azb =ay−bxc
CMR : x : y : z = a : b : c
Cho a/b = c/d . các số x,y,z,t thỏa mãn xa+yb khác 0 và zc+td khác 0
chứng minh rằng xa + yb / za+tb = xc+yd/zc+td
bạn tham khảo ở link sau nha :
https://olm.vn/hoi-dap/detail/235909931896.html
cho a/b=c/d. Các số x;y;z;t thỏa mãn: xa+yb khác 0 và zc+td khác 0. chứng minh xa+yb/za+tb=xc+yd/zc+td
Chứng minh rằng :
bz -cy /a = cx-az/b = ay-bx
bz -cy /a = cx-az/b = ay-bx/c hay bz -cy /a = cx-az/b = ay-bx vậy bn
Đúng 0
Bình luận (0)
Biết rằng :bz-cy/a=cx-az/b=ay-bx/c. Chứng minh rằng x:y:z=a:b:c
cho \(\dfrac{cy-bz}{x}=\dfrac{az-cx}{y}=\dfrac{bx-ay}{z}\) chứng minh rằng :\(\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}\)
Ta có :
\(\dfrac{cy-bx}{x}=\dfrac{az-cx}{y}=\dfrac{bx-ay}{z}=\dfrac{bxz-cxy+cxy-ayz+ayz-bxz}{ax+by+cz}=0\)
\(\Rightarrow\dfrac{cy-bz}{x}=0\) \(\Rightarrow cy=bz\) \(\Rightarrow\) \(\dfrac{b}{y}=\dfrac{c}{z}\left(1\right)\)
\(\Rightarrow\dfrac{az-cx}{y}=0\) \(\Rightarrow az=cx\) \(\Rightarrow\dfrac{a}{x}=\dfrac{c}{z}\left(2\right)\)
Từ (1) và (2) suy ra : \(\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}\)
Đúng 2
Bình luận (0)
biết rằng bz-cy/a = cx-az/b = ay-bx/c
chứng minh x:y:z = a:b:c
Vì bz-cy/a=cx-az/b=ay-bx/c
=> a(bz-cy)/a^2=b(cx-az)/b^2=c(ay-bx)/c^2
=> abz-acy/a^2=bcx=baz/b^2=cay-cbx/c^2
theo tính chất của dãy tỉ số bằng nhau :
=> abz-acy/a^2=bcx=baz/b^2=cay-cbx/c^2=a^2+...
= 0/a^2+b^2+c^2=0
vì bz-cy/a=0=>bz=cy=>y/b=z/c (1)
vì cx-az/b=0=>cx=az=>x/a=z/c (2)
từ (1) và (2) => x/a=y/b=z/c
Đúng 0
Bình luận (0)
Cho dãy tỉ số bz-cy/a × cx-az/b × ay-bc/c
Chứng Minh Rằng : x/a=y/b=z/c
Câu hỏi của GT 6916 - Toán lớp 7 - Học toán với OnlineMath tham khảo
Đúng 0
Bình luận (0)




















