Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
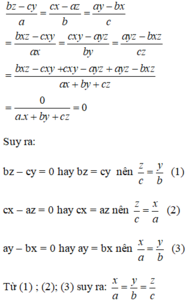
Hay x : y : z = a : b : c
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
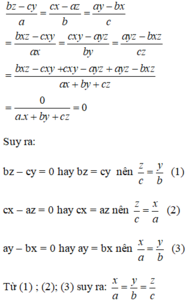
Hay x : y : z = a : b : c
Cho a + b + c = a2 + b2 + c2 = 1 và x : y : z = a : b : c.
Chứng minh rằng: (x + y + z)2 = x2 + y2 + z2.
Chứng minh rằng: Nếu a(y + z) = b(z + x) = c(x + y), trong đó a; b; c là các số khác nhau và khác 0 thì:
\(\frac{y-z}{a\left(b-c\right)}=\frac{z-x}{b\left(c-a\right)}=\frac{x-y}{c\left(a-b\right)}\)
Cho các số hữu tỉ : \(x=\frac{a}{b};y=\frac{c}{d};z=\frac{a+c}{b+d}\)(a,b,c,d thuộc Z ;b>0 ;d>0 ). Chứng minh rằng;nếu x<y thì x<z<y
1. Tìm 2 số hữu tỉ a,b biết:
a - b = 2 (a + b) = a : b
2. Cho các số a, b, c, x, y, z
\(\frac{x}{a}\)= \(\frac{y}{b}\)= \(\frac{z}{c}\)Chứng minh rằng: \(\frac{bx-cy}{a}\)= \(\frac{cx-az}{y}\)= \(\frac{ay-bx}{c}\)
a) Giả sử x=\(\frac{a}{m}\) ,y= \(\frac{b}{m}\)(a, b,m € Z,m>0).Hãy chứng tỏ rằng nếu chọn z=\(\frac{a+b}{2m}\)thì ta có x<y<z.
Hướng dẫn: Sử dụng tính chất : Nếu a, b, c € Z và a<b thì a+c< b + c
b)Hãy chọn ba phân số nằm xen giữa các phân số\(\frac{1}{2}\)và\(\frac{5}{2}\)
Cho a(y+z)=b(z+x)=c(x+y).Chứng minh y-z/a(b-c)= z-x/b(c-a) = x-y/ c(a-b)
cho a, b, c, x, y, z khác 0 thỏa mãn: x/a = y/b = z/c chứng minh: a^2/x + b^2/y + c^2/z +(a+b+c)^2/x+y+z
Chứng minh rằng nếu có : a(y+z) = b(z+x) = c(x+y) . Trong đó a , b , c là các số khác nhau và khác 0 thì y-z / a(b-c) = z-x / b(c-a) = x-y /c(a-b)
Cho các số a, b, c khác 0 và đôi một khác nhau thỏa mãn: a(z-y) = b(z+x) = c(x-y). Chứng minh rằng (y+z)/a(c-b) = (z-x)/b(c-a) = (x+y)/c(a-b).