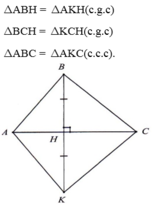
cho tam giác abc , kẻ ah vuông góc bc (h thuộc bc ) . trên tia đối của ha , ;ấy k sao cho hk = ha . chứng minh tam giác abc = tam giác kbc
Những câu hỏi liên quan
Cho tam giác ABC, kẻ AH vuông góc với BC, ( H thuộc BC ). Trên tia đối của tia HA lấy điểm K sao cho HK = HA, nối KB, KC. Tìm các cặp tam giác bằng nhau.
Cho tam giác ABC, kẻ AH vuông góc với BC,(H thuộc BC). Trên tia đối của tia HA lấy điểm K sao cho HK = HA, nối KB, KC. Tìm các cặp tam giác bằng nhau.
Cho tam giác ABC , từ A kẻ AH vuông góc với BC (H thuộc BC). Trên tia đối của tia HA lấy điểm M sao cho HA = HM . Chứng minh rằng:
a) Tam giác AHC = Tam giác MHC
b) Tam giác ABC = Tam giác MBC
Mình cần gấp
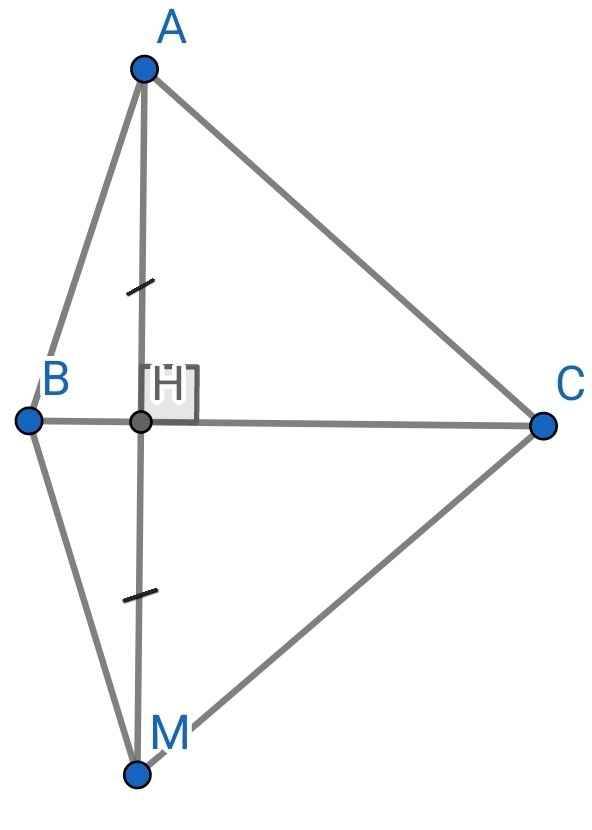a) Xét hai tam giác vuông: ∆AHC và ∆MHC có:
HC là cạnh ccung
AH = MH (gt)
⇒ ∆AHC = ∆MHC (hai cạnh góc vuông)
b) Do ∆AHC = ∆MHC (cmt)
⇒ ∠ACH = ∠MCH (hai góc tương ứng)
AC = MC (hai cạnh tương ứng)
Do ∠ACH = ∠MCH (cmt)
⇒ ∠ACB = ∠MCB
Xét ∆ABC và ∆MBC có:
AC = MC (cmt)
∠ACB = ∠MCB (cmt)
BC là cạnh chung
⇒ ∆ABC = ∆MBC (c-g-c)
Đúng 0
Bình luận (0)
Cho tam giác ABC có 3 góc đều nhọn, kẻ AH vuông góc với BC (HBC). Trên tia đối của tia HA lấy điểm D sao cho HA HD.Cho tam giác ABC có 3 góc đều nhọn, kẻ AH vuông góc với BC (HBC). Trên tia đối của tia HA lấy điểm D sao cho HA HD.
Đọc tiếp
Cho tam giác ABC có 3 góc đều nhọn, kẻ AH vuông góc với BC (H
BC). Trên tia đối của tia HA lấy điểm D sao cho HA = HD.Cho tam giác ABC có 3 góc đều nhọn, kẻ AH vuông góc với BC (HBC). Trên tia đối của tia HA lấy điểm D sao cho HA = HD.
Cho tam giác ABC, kẻ ah vuông góc với BC ( H thuộc BC ) .Trên tia đối của tia HA , lấy điểm K sao cho HK=HA. Nối KB, KC . tÌM CÁC CẶP TAM GIÁC BẰNG NHAU TRONG HÌNH
các cặp tam giác bằng nhau là
ACH=CHK
ABH=HBK
ABC=BCK
ACK=ABK(nó chỉ đúng khi góc B và góc C của tam giác ABC có số đo góc bằng nhau)
Mình cũng chx nghĩ ra đáp án nên bn chờ lâu lâu thêm tí nữa đi bởi vì mình nhìn bài lm của bạn kia là biết lm sai r đấy
Đúng 0
Bình luận (0)
cho tam giác ABC kẻ AH vuông góc với BC [H thuộc BC] trên tia đối của tia HA lấy điểmK sao cho HK=HA với KB,KC cung các cặp tam giác bằng nhau trong hình vẽ
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC,H thuộc
BC. Lấy D thuộc đoạn AH. Trên tia đối của tia HA lấy điểm E sao cho
HE=AD. Đường vuông góc với AH tại D cắt AC tại F. Chứng minh EB vuông
góc với EF.
Xét DEF vuông tại D
EF2 = DE2 + DF2 (định lí Phythagoras)
Xét BHE vuông tại H
BE2 = BH2 + HE2 (định lí Phythagoras)
Xét ABH vuông tại H
AB2 = AH2 + BH2 (định lí Phythagoras)
Xét AFD vuông tại D
AF2 = AD2 + DF2 (định lí Phythagoras)
Xét ABF vuông tại A
BF2 = AB2 +AF2 (định lí Phythagoras)
BF2 = AH2 +BH2 +AD2 +DF2
BF2 = (AD + DH)2 + (BH2 +AD2) + DF2
BF2 = (HE +DH)2 +(BH2 + HE2) + DF2
BF2 = DE2 + BE2 + DF2
BF2 = (DE2 + DF2) + BE2
BF2 = EF2 + BE2
Xét BEF có: BF2 = EF2 + BE2
BEF vuông tại E (định lí Phythagoras)
BEF = 90o
EB EF (đpcm)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Câu hỏi: Cho tam giác ABC vuông tại A, kẻ AH vuông góc BC (H thuộc BC) Trên tia AH lấy điểm E sao cho HA=HE. Trên tia đối của tia CB lấy điểm F sao cho BC=CF. Gọi M là trung điểm EF.
a) Chứng minh rằng tam giác ABH=tam giác ACH.
b) Cho AB=10cm, AH=8cm. Tính độ dài BC.
c) Chứng minh rằng ba điểm A, C, M thẳng hàng.
CHO TAM GIÁC ABC VUÔNG GÓC VỚI A, KẺ AH VUÔNG GÓC VỚI BC (H VUÔNG GÓC VỚI BC).TRÊN TIA ĐỐI CỦA TIA HA LẤY ĐIỂM D SAO CHO HD=AH
a,CM: TAM GIÁC AHB=TAM GIÁC DHB
b, BD=CD
a) Xét ΔAHB vuông tại H và ΔDHB vuông tại H có
BH chung
AH=DH(gt)
Do đó: ΔAHB=ΔDHB(hai cạnh góc vuông)
Đúng 0
Bình luận (0)